1.4. Основна теорема алгебри

Основна теорема алгебри. Будь-який многочлен степеня n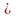 1 має принаймні один, взагалі кажучи, комплексний корінь.

Традиційне доведення цієї теореми використовувало наступні леми, які мають самостійний інтерес.

Наведемо їх без доведення.

Лема 1. (Лема про вищий член многочлена).

Нехай задано многочлен f(z)= a₀zⁿ+ a₁ z^n-1+ a₂ z^n-2+...+a_n степеня n 1 і задано число k>0, тоді таке існує число P, що як тільки 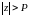, то

.

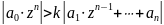Лема2. (Лема про зростання модуля многочлена).

Нехай задано многочлен f(z)= a₀zⁿ+ a₁ z^n-1+ a₂ z^n-2+...+a_n степеня n 1 і задано число М>0. Тоді існує число P>0 таке, що як тільки , то .

Лема 3. (Лема Д’Аламбера).

Нехай задано многочлен f(z)= a₀zⁿ+ a₁ z^n-1+ a₂ z^n-2+...+a_n степеня n 1 і задано число z₀, що не є коренем многочлена f(z). Тоді існує таке число h, що .

Розглянемо наслідки основної теореми алгебри.

Наслідок 1. Многочлен n-го степеня має n коренів, де кожен корінь враховують таку кількість разів, яка дорівнює цього кратності.

Доведення. Розглянемо деякий многочлен f(z)=a₀zⁿ+ a₁ z^n-1+ a₂ z^n-2+...+a_n. При n=0 многочлен має вигляд 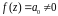і очевидно не має жодного кореня, тобто має 0 коренів.

Розглянемо випадок, коли n 1. Тоді за основною теоремою алгебри многочлен f(z) має принаймні один корінь

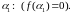
Застосуємо наслідок з теореми Безу:

Якщо степінь , то теорему доведено. Якщо степінь , то застосуємо основну теорему алгебри:

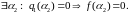
Продовжуючи таким чином, отримаємо

Отже, наслідок доведено. Зауважимо, що .

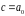Мимохідь ми довели наслідок 2.

Наслідок 2. Будь-який многочлен можна розкласти на лінійні множники в області комплексних чисел.

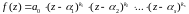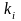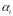, де – кратність кореня ,s n.

Наслідок 3. Нехай задано два многочлени f(z) і g(z) степенів n 1, значення яких збігається в n+1 точці, тобто

................................

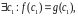
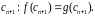
Тоді многочлени f(z) і g(z) є рівні (у формально-алгебраїчному сенсі).

Доведення. Припустимо супротивне. Нехай f(z) g(z). Тоді утворимо многочлен h(z)=f(z)–g(z) (при цьому очевидно, що степінь h(z) n). Згідно з наслідком 1 основної теореми алгебри многочлен h(z) мусить мати не більше, ніж n коренів. Але існує n+1 точка, яка задовольняє умову h(z)=0. Тому многочлен h(z) має n+1 корінь. Маємо суперечність, яка і доводить наслідок 3.

Застосовуючи наслідок 3 можна довести еквівалентність двох підходів до поняття рівності многочленів. Раніше ми довели, якщо многочлени рівні у формально-алгебраїчному сенсі, то вони рівні і в теоретико-функціональному. Доведемо обернене. Степені многочленів є менші за деяке число n або дорівнюють йому, а многочлени збігаються в нескінченній множині точок. Виберемо серед них n+1 точку і застосуємо наслідок 3 основної теореми алгебри.

1.5. Формули Вієта

Формули Вієта встановлюють зв’язок між коренями многочлена та його коефіцієнтами. Нехай задано многочлен (а₀=1)

_.

За наслідком 1 даний многочлен має в комплексній області n коренів. Нехай – корені многочлена f(z). Тоді за наслідком 2 основної теореми алгебри його можна подати у вигляді

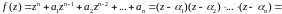
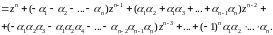
Порівняємо коефіцієнти при однакових степенях многочлена:

1=1,

..................................................................................................

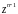
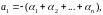
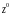
Розглянемо окремий випадок при n=2:

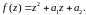
Згідно з формулами Вієта

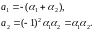
Отримали формули, відомі з шкільного курсу.