9.4. Ізоморфізм векторних та евклідових просторів

Нехай задано два векторні простори 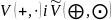над одним і тим же полем Р.

Означення 1. Два векторні простори називають ізоморфними, якщо існує взаємно однозначне відображення 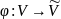, для якого виконуються такі умови:

1) якщ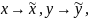о то ;

2) .

Із наведеного означення випливає, що 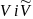відносно операції додавання є ізоморфні як групи. Тому, як випливає з означення при будь-якому ізоморфізмі φ мають місце такі властивості: 1) нульовий вектор простору відображується в нульовий вектор простору ; 2) якщо то .

Теорема 1. Векторні простори однієї і тієї ж вимірності ізоморфні між собою.

Доведення. Нехай векторні простори і мають одну й ту ж вимірність n.

Задамо у цих просторах базиси:

– базис ,

– базис .

Побудуємо відображення φ: за таким правилом: вектору

поставимо у відповідність вектор

.

Доведемо, що відображення φ – ізоморфізм.

Якщо , то .

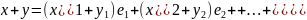Тоді φ відображує цей вектор

.

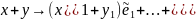
Аналогічно, можна довести, що .

Отже, φ – ізоморфізм.

Ізоморфізм векторних просторів означає їх однакову структуру і окреслює найбільш суттєві властивості (і відволікає від конкретного змісту множин, із яких утворюється векторний простір).

Отже, основна характеристика векторного простору є його вимірність. Це можна стверджувати і щодо евклідових просторів.

Означення 2. Два евклідові простори 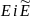називають ізоморфними, коли існує таке взаємно однозначне відображення φ : , що

якщо , то виконуються такі умови:

1) то

2)

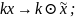
3)

Із перших двох умов випливає, що евклідові простори є ізоморфні як лінійні простори і встановлений ізоморфізм зберігає скалярний добуток.

Теорема 2. Усі евклідові простори однакової вимірності n ізоморфні.

Доведення. Побудуємо відображення φ так само, як і в ході доведення теореми 1, але за умови, що задані базиси ортонормовані. Тоді умови 1-ша і 2-га умови означення 2, як було доведено, виконуються. Доведемо виконання 3-ої умови.

Обчислимо

.

Отже, всі вимоги означення 3 виконуються. Теорему доведено.

10. Лінійні оператори в евклідовому просторі

10.1. Зв’язок між білінійними формами і лінійними операторами в евклідовому просторі. Спряжені оператори

Нехай в евклідовому просторі Eⁿ задано білінійну форму А(х,у) і – ортонормований базис цього простору. За допомогою координатного запису, білінійну форму можна подати так:

(10.1.1)

де 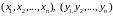– координати векторів х та у відповідно.

_{Побудуємо вектор} z із координатами

(10.1.2)

Тоді рівність (10.1.1) можна записати в вигляді

Застосовуючи вираз скалярного добутку через координати векторів в ортонормованому базисі, маємо

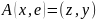. (10.1.3)

Із формул (10.1.2) випливає, що вектор z отримано з вектора х під дією деякого лінійного оператора з матрицею

Отже, і рівність (10.1.3) можна записати у вигляді

(10.1.4)

Застосовуючи координатний запис білінійної форми, можна також отримати

(10.1.5)

Побудуємо вектор z* із координатами z1, z2, …zn:

(10.1.6)

Із рівності (10.1.5) отримаємо

(10.1.7)

Із формул (10.1.6) випливає, що вектор z^* отримано з вектора у під дією деякого лінійного оператора 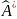з матрицею в заданому базисі

Тоді рівність (10.1.7) можна записати так:

(10.1.8)

Таким чином, із кожною білінійною формою в евклідовому просторі можна пов’язати два лінійні оператори , матриці яких отримують одна з іншої транспонуванням.

Означення. Оператор називають спряженим із лінійним оператором , якщо

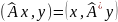. (10.1.9)

Встановлюючи зв’язок між білінійною формою і лінійними операторами, мимохідь отримали такі твердження (див. (10.1.3), (10.1.8)):

1. Для кожного лінійного оператора в евклідовому просторі існує спряжений.

2. Матриця оператора в ортонормованому базисі може бути отримана з матриці оператора транспонуванням.