6.2. Ізоморфізм груп

Нехай задано дві групи:G з груповою операцією * і група із операцією (позначатимемо їх G * , ).

Означення. Групи G * і називають ізоморфними, якщо існує таке взаємно однозначне відображення , яке задовольняє умову:

якщо

то .

Саме відображення називають ізоморфізмом.

Відзначимо деякі властивості ізоморфізму.

Властивість 1. За будь-якого ізоморфізму нейтральному елементу групи G * відповідає нейтральний елемент групи .

Доведення. Нехай е – нейтральний елемент групи G *, а – нейтральний елемент групи . За ізоморфізму

Тоді за означенням ізоморфізму

але .

Отже внаслідок однозначності маємо .

Із цього за означенням нейтрального елемента випливає, що .

Властивість 2. За будь-кого ізоморфізму , елемент, обернений до елементах відображається в елемент, обернений до образу цього елемента. Тобто, якщо , то .

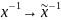Доведіть властивість самостійно.

Приклад 1. Доведемо, що будь-яка циклічна група нескінченного порядку ізоморфна адитивній групі Z цілих чисел. Нехай G * – циклічна група нескінченого порядку:

адитивна група цілих чисел.

Задамо взаємно однозначне відображення за таким правилом:

.

Доведіть самостійно, що – ізоморфізм, тобто

якщо ,

,

то .

Приклад 2. Будь-яка циклічна група порядку n ізоморфна мультиплікативній групі коренів n-го степеня з одиниці.

Доведення аналогічне прикладу 1.

Аналіз попередній прикладів приводить до висновку, що всі циклічні групи нескінченого порядку ізоморфні між собою, ізоморфні між собою також усі циклічні групи одного і того ж скінченого порядку n.

6.3. Поняття кільця

Означення. Непорожню множину називають кільцем, якщо в ній визначено дві бінарні внутрішні алгебраїчні операції, додавання і множення.

Відносно першої операції є абельовою групою, друга операція асоціативна, обидві операції пов’язані законом дистрибутивності, тобто:

1. .

2. .

3. .

4. .

5. .

6. .

7. ( .

8. .

Означення. Якщо в кільці відносно операцій множення існує нейтральний елемент, то його називають одиницею, а кільце називають кільцем із одиниці.

Означення. Якщо операція множення комутативна, то кільце називають комутативним.

Означення. Два елементи кільця називають дільниками нуля, якщо .

Означення. Кільце називають кільцем із дільниками нуля, якщо в ньому є дільники нуля.

Приклад 1. Множина натуральних чисел відносно стандартних операцій додавання і множення не є кільцем через невиконання умов 3.,4. означення кільця.

Приклад 2. Множина Z відносно звичайного додавання і множення є кільцем, причому з одиницею, комутативне, без дільників нуля.

Приклад 3. Множина Q відносно звичайного додавання і множення є комутативне кільце з одиницею без дільників нуля.

Приклад 4,5. Множина дійсних чисел R (комплексних чисел) відносно стандартних операцій додавання і множення – комутативні кільця з одиницею, без дільників нуля

Приклад 6. Множина всіх квадратних матриць n-го порядку є кільце з одиницею, некомутативне, з дільниками нуля. Доведемо, що в цьому кільці є дільники нуля.

Розглянемо дві матриці, ненульові, порядку n=2:

А= .

Приклад 7. Множина всіх многочленів відносно операцій додавання і множення є комутативне кільце з одиницею, без дільників нуля.

Приклад 8. Множина всіх неперервних функцій, визначених на всій дійсній осі є комутативне кільце з одиницею та дільниками нуля.

Побудуємо дільники нуля:

. Але .

Приклад 9. Розглянемо множину з одного елемента . Це – кільце комутативне з одиницею, без дільника нуля (одиниця цього кільця є 0). Таке кільце називають нульовим.

Приклад 10. Розглянемо множину . Операцію додавання і множення введемо табличним способом:

	0	1			0	1
0	0	0		0	0	1
1	0	1		1	1	0

Легко перевірити, що це є кільце з одиницею, комутативне, без дільників нуля. Дане кільце називають кільцем лишків за модулем 2.

Побудуємо кільце лишків за модулем .

Розглянемо множину всіх цілих чисел і побудуємо на базі цієї множини множину, що складається з елементів. Для цього візьмемо натуральне . Усі цілі числа поділимо на число n.

До нульового класу включимо всі цілі числа, які внаслідок ділення на дають остачу нуль, і позначимо цей клас . До нього входять числа , де – будь-яке ціле число. Аналогічно до першого класу включимо числа , які внаслідок ділення на дають остачу одиницю. Позначимо цей клас . Продовжуючи аналогічно, пронумеруємо всі класи до -го включно. Клас складається з чисел, які в результаті ділення на дають остачу .

Введемо в отриману множину з n елементів операції додавання та множення. Розглянемо множину

; ; ; ; .

Для цього візьмемо по представнику з класів С_к і С_m і з’ясуємо,в які класи потрапить їх сума й добуток.

Покажемо що доцільно додавання ввести так:

Насправді та .

Тоді :

а) якщо ;

б) якщо .

Аналогічно можна показати, що множення класів доцільно ввести за таким правилом: , де – остача від ділення числа на число n.

Легко довести, що дана множина відносно введених операцій є кільце. Це кільце називають кільцем лишків за модулем n.

Крім того, можна довести, якщо – складене число, то кільце лишків за модулем має дільники нуля.