5. Криві й поверхні другого порядку

5.1. Дослідження кривих і поверхонь другого порядку за їх канонічним рівнянням Дослідження цього питання здійснюється за таким планом:

П Л А Н

І. Дослідження кривих другого порядку

1. Еліпс

1.1. Означення і виведення канонічного рівняння

1.2. Дослідження форми, ексцентриситет, директриси

1.3. Полярне рівняння

2. Гіпербола

2.1. Означення і виведення канонічного рівняння

2.2. Дослідження форми, ексцентриситет, директриси, асимптоти

2.3. Полярне рівняння

3. Парабола

3.1. Означення і виведення канонічного рівняння

3.2. Дослідження форми, ексцентриситет, директриса

3.3. Полярне рівняння

4. Інші властивості

ІІ. частина

Дослідження поверхонь другого порядку за допомогою перерізів, паралельних координатним площинам:

1) еліпсоїда за його канонічним рівнянням ;

2) однопорожнинного гіперболоїда 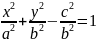та двопорожнинного – ;

3)еліптичного параболоїда та гіперболічного ;

4)конуса ;

5) циліндрів еліптичного , гіперболічного , параболічного .

5.2. Перетворення рівняння кривої при зміні прямокутної системи

Домовимось записувати рівняння кривої другого порядку у вигляді

(5.2.1)

Розглядатимемо лише перехід від однієї прямокутної системи до іншої прямокутної. Як відомо для таких систем суттєво різними є два перетворення:

• паралельний перенос початку;

• поворот осей координат.

За таких переходів на основі теореми про інваріантність порядку ми будемо отримувати рівняння такого ж вигляду.

Перетворення рівняння кривої другого порядку при переносі початку

Нехай у прямокутній системі координат O крива має вигляд рівняння (5.2.1), здійснимо перенесення початку (Рис. 11). Відомо, що у випадку перенесення початку в точку О’(х₀,у₀) координати точки перетворюються за правилом

(5.2.2)

У другій системі координат одержимо рівняння

(5.2.1^/)

Постановка задачі. Знайти зв’язок чисел .

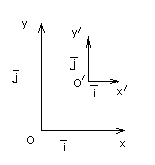
Рис. 11

Підставимо формули (5.2.2) у рівність (5.2.1):

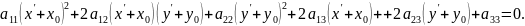(5.2.3)

Порівняємо коефіцієнти рівнянь (5.2.3) і (5.2.1).

К оефіцієнт при =

(5.2.4)

(5.2.5)

вільний член

(5.2.6)

Зауважимо, що а₃₃=f(x₀,y₀). Отже, у разі переносі початку не змінюються коефіцієнти при членах другого вимірювання. Інші коефіцієнти змінюються за законом (5.2.4), (5.2.5) і (5.2.6).

Перетворення рівняння кривої другого порядку при повороті осей

Нехай в деякій систему координат О, крива має рівняння (5.2.1). Здійснимо поворот осей координат на кут (Рис. 12). Нехай в отриманій системі координат рівняння набуває вигляду (5.2.2). Треба знайти зв’язок між і .

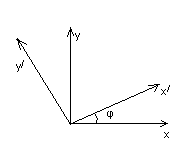
Рис. 12

Відомо, що при повороті осей на кут координати точки змінюються за законом

Підставимо ці формули в рівняння (5.2.1):

.

Після розкриття дужок можна переконатися, що коефіцієнти при , , тобто коефіцієнти можуть бути виражені лише через , , , а коефіцієнти при та 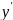, тобто коефіцієнти та – лише через , , .

Знайдемо коефіцієнт при .

+2 .

Доведемо, що завжди існує поворот на такий кут , за якого в перетвореному рівнянні (2) зникає член, що містить , тобто Для цього треба довести, що тригонометричне рівняння

+2 (5.2.7)

має розв’язок. Це рівняння можна записати в такому вигляді:

( )sin2 2 =0,

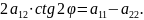
Розглянемо два випадки для а₁₂:

1. тоді . Звідси визначимо кут 2:

2. Якщо , то вже в початковому рівнянні (5.2.1) немає попарного добутку.

Практично поворот на кут краще знаходити іншим способом. Для цього запишемо рівняння (5.2.7) у такому вигляді:

+ =0.

Поділимо його на :

Взагалі існує два розв’язки і . Візьмемо будь-який із них. Позначимо вибраний тангенс через . Тоді для знаходження формули повороту за формулою 1+ знайдемо 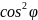. Маємо два значення для . Виберемо одне зі значень, тоді Таким чином отримаємо формули повороту. Отже, поворот знайдено.