
- •1. Теорія многочленів
- •1.1. Поняття многочлена, алгебра многочленів
- •1.2. Ділення многочленів з остачею. Найбільш спільний дільник (нсд)
- •1.3. Корені многочленів
- •1.4. Основна теорема алгебри
- •1.5. Формули Вієта
- •1.6. Дослідження многочленів з дійсними коефіцієнтами
- •2. Перетворення координат вектора при зміні базису, перетворення координат точки при зміні системи координат
- •2.1. Перетворення координат вектора
- •2.2. Перетворення координат точки геометричного простору (площини) при зміні системи координат
- •2.3. Перетворення координат точки площини при зміні прямокутної системи координат
- •3. Лінії і поверхні
- •3.1. Поняття рівняння лінії, рівняння поверхні
- •3.2. Параметричні рівняння лінії та поверхні
- •3.3. Алгебраїчні лінії та поверхні
- •4. Геометричні образи лінійних рівнянь
- •4.1. Загальні рівняння площини і прямої на площині
- •4.2. Способи задання прямої на площині
- •4.3. Способи задання площини
- •4.4. Умови паралельності та збіжності двох прямих на площині
- •4.5. Умови паралельності та збіжності двох площин
- •4.6. Пряма в просторі
- •5. Криві й поверхні другого порядку
- •5.1. Дослідження кривих і поверхонь другого порядку за їх канонічним рівнянням Дослідження цього питання здійснюється за таким планом:
- •5.2. Перетворення рівняння кривої при зміні прямокутної системи
- •5.3. Інваріанти кривої другого порядку. Класифікація кривих
- •5.4. Спрощення центральних кривих
- •5.5. Спрощення нецентральних кривих
- •6. Алгебраїчні структури
- •6.1. Поняття групи
- •6.2. Ізоморфізм груп
- •6.3. Поняття кільця
- •6.4. Поняття тіла, поля, алгебри
- •7. Лінійний оператор
- •7.1. Лінійний оператор. Матриця лінійного оператора
- •7.2. Характеристична матриця. Характеристичний многочлен. Характеристичні корені даної матриці
- •7.3. Власні вектори та власні значення лінійного оператора
- •7.4. Жорданова форма матриці
- •7.5. Алгебра лінійних операторів
- •8. Лінійні та білінійні форми
- •8.1. Поняття лінійної і білінійної форм
- •8.2. Матриця білінійної форми в заданому базисі Координатний запис білінійної форми
- •8.3. Квадратична форма в дійсному просторі
- •9. Евклідів простір
- •9.1. Поняття скалярного добутку
- •9.2. Основні метричні поняття в евклідовому просторі
- •9.3. Процес ортогоналізації
- •9.4. Ізоморфізм векторних та евклідових просторів
- •10. Лінійні оператори в евклідовому просторі
- •10.1. Зв’язок між білінійними формами і лінійними операторами в евклідовому просторі. Спряжені оператори
- •10.2. Деякі класи лінійних операторів у евклідовому просторі
- •10.2.1. Самоспряжені (симетричні) оператори
- •10.2.2. Поняття ортогонального оператора
- •10.3. Зведення квадратичної форми до канонічного вигляду шляхом переходу до нового ортонормованого базису
- •10.4. Застосування до теорії поверхонь другого порядку
- •Список рекомендованої літератури
Вступ
Конспект лекцій містить теоретичний матеріал другого семестру курсу "Алгебра та геометрія" для студентів першого курсу факультету прикладної математики. Як і в першому семестрі, при викладанні обрано шлях взаємного доповнення і проникнення алгебраїчних і геометричних питань.
Другий семестр починається з теорії многочленів, яка на протязі багатьох сторіч була центральним питанням алгебри. В той час алгебра вважалась наукою про розв’язування алгебраїчних рівнянь. Було знайдено формули розв'язків рівнянь першого, другого, третього та четвертого степеня. Потім почались марні пошуки формул для рівнянь вище четвертого степеня. Тоді виникає головне питання, чи, взагалі, існують корені. Відповідь було отримано в XIX сторіччі доведенням основної теореми: корені існують і їх слід шукати серед комплексних чисел. Студенти вже підготовлені до сприйняття цього, оскільки комплексні числа вивчались в першому семестрі.
Далі чисто алгебраїчні питання многочленів знаходять продовження в теорії алгебраїчних ліній і поверхонь. Ретельно вивчаються геометричні образи многочленів від двох і трьох змінних першого і другого степенів. А саме, вивчаються прямі на площині, площини, прямі в просторі. Розглядається загальна теорія кривих другого порядку.
В XIX сторіччі роботи молодих математиків Абеля і Галуа сприяли оформленню нових поглядів на алгебру. При розв’язанні основної на той час задачі вони створили нове поняття і пов’язану з ним теорію груп. Сучасна алгебра – це наука про властивості алгебраїчних операцій в множині довільної природи. Першокурсникам сучасна алгебра подається елементарною теорією груп, кілець, полей (алгебраїчних структур).
На протязі всього курсу поняття лінійного простору (введеного в першому семестрі) двічі узагальнювалась. Після введення поняття поля вводиться поняття лінійного оператора, його матриці. Наводяться приклади, які показують, що це поняття знаходить місце в різних галузях математики. Але алгебра формалізує його за допомогою матриць. З лінійним оператором пов’язані поняття власних векторів і власних значень, які знаходять застосування в подальшому в інших дисциплінах. Це поняття дозволяє поставити питання про найпростіший вигляд, до якого може бути зведена матриця лінійного оператора. Так першокурсники знайомляться з діагональною і жордановою формою матриці.
В курс "Алгебра та геометрія" входять також лінійні, білінійні, квадратичні форми. Цікавим є питання евклідового простору. Він є узагальненням геометричного простору, в ньому можна визначити довжину, кут між векторами.
В евклідовому просторі розглядаються важливі класи лінійних операторів (самоспряжені і ортогональні оператори). За допомогою цих операторів розв’язуються питання про зведення квадратичної форми до канонічного вигляду. Отриманий алгебраїчний результат застосовується до геометричного питання теорії поверхонь. Таким чином, при викладанні матеріалу формально-алгебраїчний підхід чергується з геометричною інтерпретацією.
1. Теорія многочленів
1.1. Поняття многочлена, алгебра многочленів
Існують два погляди на поняття многочлена: формально-алгебраїчний і теоретико-функціональний.
Означення (формально-алгебраїчне). Многочленом відносно змінної z називають суму цілих невід’ємних степенів z, взятих з деякими коефіцієнтами.
Означення
(теоретико-функціональне).
Многочлен
– це функція спеціального вигляду:
 a₀zⁿ
+a₁
zn-1+…+an
,
a₀zⁿ
+a₁
zn-1+…+an
, .
.
Змінну z і коефіцієнти вважатимемо комплексними. Найбільш поширені такі форми запису многочлена:
a₀+a₁z+a₂z²+…+anzⁿ– за зростаючими степенями;
a₁zⁿ +a₂zn-1+…+an-1z+an – за спадними степенями.
Означення.
Степенем
многочлена
 називають найвищий показник,
із
яким z
входить до многочлена з коефіцієнтом,
який не дорівнює 0.
називають найвищий показник,
із
яким z
входить до многочлена з коефіцієнтом,
який не дорівнює 0.
Над многочленами здійснюють дві основні алгебраїчні операції: додавання і множення. Застосуємо форму запису многочлена за зростаючими степенями.
Означення.
Сумою
многочленів
a₀+a₁z+a₂z²+…+anzⁿ
і
 b₀+b₁z+b₂z²+…+bszs
називають
многочлен
+
b₀+b₁z+b₂z²+…+bszs
називають
многочлен
+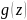 із
коефіцієнтами сі
такими,
що сі=aі+bі..
із
коефіцієнтами сі
такими,
що сі=aі+bі..
Означення.
Добутком
і
називають многочлен
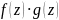 ,
коефіцієнти якого обчислюють за таким
правилом:
,
коефіцієнти якого обчислюють за таким
правилом:
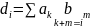
Із цього правила випливає правило множення многочленів як двох сум.
Означення (формально-алгебраічне). Два многочлена називають рівними, якщо вони мають однакові коефіцієнти при однакових степенях z.
Означення (теоретико-функціональне). Дві функції (у тому числі й многочлен) називають рівними, якщо: 1) у них однакові області визначення; 2) за однакових значень аргументу вони набувають однакових значень.
Властивості операцій:
1) + = + – комутативність додавання;
2)
(
+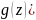 +
h
+
h =
+
=
+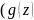 +
h
)
– асоціативність додавання;
+
h
)
– асоціативність додавання;
3)
= –
комутативність множення;
–
комутативність множення;
4)
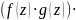 h
h h
h –асоціативність
множення;
–асоціативність
множення;
5)
 h
=
h
=
 h
+
h
+
 h
– дистрибутивність.
h
– дистрибутивність.
Зрозуміло, якщо многочлени рівні формально-алгебраїчному сенсі, то рівні вони і в теоретико-функціональному. Обернене не очевидно. Ми доведемо цей факт пізніше, застосувавши наслідок основної теореми.
З’ясуємо
питання про існування операцій обернених
додаванню і множенню. Для цього застосуємо
поняття оберненої операції до загальної
внутрішньої операції
 .
.
Візьмемо
за операцію
операцію додавання:
=
+ . Встановимо чи існує для заданих
 (z)
й
g(z)
такий многочлен h(z),
що g(z)+h(z)=
(z).
Позначимо h(z)=
(z)
й
g(z)
такий многочлен h(z),
що g(z)+h(z)=
(z).
Позначимо h(z)=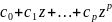 .
Тоді
.
Тоді
 .
Звідси
.
Звідси
 .
Отже, такий многочлен h(z)
існує.
.
Отже, такий многочлен h(z)
існує.
Візьмемо
за операцію
операцію множення:
= .
Доведемо, що множення не існує оберненої
операції. Проаналізувавши поняття
оберненої операції, дійдемо висновку,
що для цього достатньо навести принаймні
одну пару многочленів f(z)
й
g(z),
для яких не існує такого многочлена
h(z),
щоб g(z)
.
Доведемо, що множення не існує оберненої
операції. Проаналізувавши поняття
оберненої операції, дійдемо висновку,
що для цього достатньо навести принаймні
одну пару многочленів f(z)
й
g(z),
для яких не існує такого многочлена
h(z),
щоб g(z) h(z)=
(z).
Такими, наприклад, є
(z)=1,
g(z)=z.
Але h(z)
не многочлен. Отже, обернена множенню
операція невизначена в множині
многочленів.
h(z)=
(z).
Такими, наприклад, є
(z)=1,
g(z)=z.
Але h(z)
не многочлен. Отже, обернена множенню
операція невизначена в множині
многочленів.
1.2. Ділення многочленів з остачею. Найбільш спільний дільник (нсд)
Означення.
Поділити
многочлен f(z)
на g(z)
з остачею – це означає знайти пару таких
многочленів q(z)
і
r(z)
щоб f(z)=
g(z)
q(z) + r(z),
причому r(z)
 0
(r(z) =0
0
(r(z) =0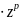 +0
+0 +…+0)
або степінь r(z)
+…+0)
або степінь r(z) g(z).
g(z).
Теорема.
Для будь-яких многочленів f(z)
й
g(z),
де g(z)≠0 +…+0,
де можливо ділення з остачею, причому
q(z)
і r(z) визначаються
однозначно.
+…+0,
де можливо ділення з остачею, причому
q(z)
і r(z) визначаються
однозначно.
Многочлен r(z) називають остачею від ділення многочлена f(z) на g(z), q(z) – часткою.
Доведіть теорему самостійно.
Означення.
Говоритимемо,
що многочлен f(z)
ділиться
на многочлен g(z)
без остачі, якщо r(z)≡0
(ділення без остачі позначатимемо так:
 .
.
Означення.
Спільним
дільником многочленів f(z)
і g(z) називають
такий многочлен
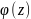 ,
на який і f(z),
і
,
на який і f(z),
і
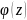 діляться
без
остачі.
діляться
без
остачі.
Означення. Найбільшим спільним дільником многочленів f(z) і g(z) називають такий їх спільний дільник, який ділиться на будь-який їх спільний дільник.
Для подальшого знаходження найбільшого спільного дільника сформулюємо властивості подільності.
1)
Якщо f(z) g(z), а g(z)
h(z),
то f(z)
h(z).
g(z), а g(z)
h(z),
то f(z)
h(z).
Доведення.
f(z) g(z)
g(z)
 f(z)=
g(z)
f(z)=
g(z) (z),
(z),
g(z)
h(z)
g(z)=h(z) (z),
(z),
f(z)=h(z)
(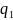 (z)
(z))=h(z)·g(z)
(g(z)=g1(z)·g2(z)),
(z)
(z))=h(z)·g(z)
(g(z)=g1(z)·g2(z)),
r(z) Отже f(z)
h(z).
Отже f(z)
h(z).
2
)Якщо f(z)
h(z) і g(z)
h(z),
то
(f(z) g(z))
h(z)
(доведіть самостійно).
g(z))
h(z)
(доведіть самостійно).
3)
Якщо f(z)
h(z) і
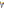 g(z), то
(f(z)
g(z))
h(z)
(доведіть самостійно).
g(z), то
(f(z)
g(z))
h(z)
(доведіть самостійно).
4) Будь-який многочлен ділиться на многочлен нульового степеня.
Доведення.
Нехай
f(z)= і h(z)=
і h(z)= .
Подаємо f(z)
у вигляді
.
Подаємо f(z)
у вигляді
f(z)= .
Отже f(z)
h(z).
.
Отже f(z)
h(z).
5)
Якщо f(z)
g(z), тоді
f(z)
с
g(z);
с-const,
c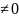 (доведіть самостійно).
(доведіть самостійно).
6) Якщо f(z) g(z) і g(z) f(z), то вони відрізняються постійним множником.
Доведення.
Оскільки f(z) g(z), то f(z)= g(z) (z), g(z) f(z), g(z)=f(z) (z).
Тоді
f(z)=f(z)
(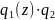 (z))
(z)=1
(z))
(z)=1
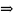 степінь
степінь
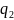 (z)
дорівнює 0 і степінь
(z)
дорівнює 0. Звідси випливає, що
(z)–const
і
(z)–const
.
(z)
дорівнює 0 і степінь
(z)
дорівнює 0. Звідси випливає, що
(z)–const
і
(z)–const
.
Отже, f(z) = с g(z).
Із наведених властивостей випливає, що найбільший спільний дільник визначають не однозначно, а з точністю до постійного множника.
Розглянемо алгоритм знаходження найбільшого спільного дільника. Нехай задано f(z) і g(z). Треба знайти найбільший спільний дільник d(z).
Опишемо процес, який називають алгоритмом Евкліда.
Застосуємо
до f(z)
і
g(z)
теорему про ділення з остачею:
(1)
f(z)=g(z
)
(2)
g(z)=
(3)
…...….
(K)
(K+1)
|
1)
2)Поділимо g(z) на остачу .
Продовжуючи
далі знайдемо таку остачу
Шукана
остача обов’язково існує, тому що
степені остач на кожному кроці
послідовно знижуються, в “найгіршому”
випадку степінь
|
Доведемо, що – найбільший спільний дільник. За означенням НСД треба довести два факти:
1)
– спільний дільник, тобто f
(z) g(z)
g(z) .
.
З
рівності (k+1)
описаного вище алгоритму Евкліда
випливає, що
 тоді з рівності (k)
маємо
тоді з рівності (k)
маємо
 аналогічно піднімаючись вище з рівностей
(3), (2), (1) маємо
аналогічно піднімаючись вище з рівностей
(3), (2), (1) маємо ,g(z)
,g(z) ,
f (z)
.
Отже,
,
f (z)
.
Отже,
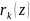 –
спільний дільник
–
спільний дільник
2)
–
найбільший спільний дільник. Нехай h(z)
довільний спільний дільник f
(z) і g(z), треба
довести, що
 .
За означенням спільного дільника f(z)
h(z) , g(z)
h(z). Тоді
з рівності (1) випливає:
=
f(z)-
g(z)
.
За означенням спільного дільника f(z)
h(z) , g(z)
h(z). Тоді
з рівності (1) випливає:
=
f(z)-
g(z)
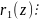 h(z). З
рівності (2) випливає, що:
(z)
h(z),
з рівності (3) випливає
(z)
h(z). Продовжуючи
таким же чином, маємо
h(z). З
рівності (2) випливає, що:
(z)
h(z),
з рівності (3) випливає
(z)
h(z). Продовжуючи
таким же чином, маємо
 h(z). Отже,
ми довели, що
–
найбільший спільний дільник.
h(z). Отже,
ми довели, що
–
найбільший спільний дільник.
Означення. Многочлени f (z) і g(z) називають взаємно простими, якщо їх спільним дільником є многочлен нульового степеня (число не рівне нулю).
Оскільки найбільший спільний дільник (НСД) визначається з точністю до постійного множника, то НСД взаємно простих многочленів можна вважати рівним 1.


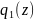 і
і
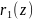 такі, що
такі, що
 +
;
+
; (z)
+
(z)
+ (z);
(z);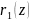 =
(z)
=
(z) (z)
+
(z)
+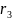 (z);
(z);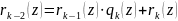 ;
;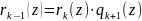 ;
;

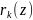 ,
на яку без остачі поділиться попередня
остача, тобто
,
на яку без остачі поділиться попередня
остача, тобто
 .
. знизиться до нуля, а на многочлен
нульового степеня поділиться будь-який
многочлен
знизиться до нуля, а на многочлен
нульового степеня поділиться будь-який
многочлен