2.2 Расчёт клиноременной передачи.

Исходные данные:

Вт; Вт – мощности на 1-м и 2-м валах;

; - вращающие моменты на 1-м и 2-м валах;

; - частоты вращения 1-го и 2-го валов;

- передаточное число;

Расчёт:

По таблице 2.2.1 [3] выбрано нормальное сечение ремня Б

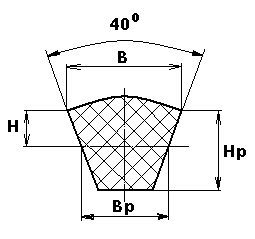
Для этого сечения: ; Кол-во ремней z: 2…6шт.;

.

Диаметр меньшего шкива должен быть на порядок больше , поэтому по таблице 2.2.4.[3] принимаем ;

Расчётный диаметр ведомого шкива:

;

Действительный диаметр (табл. 2.2.4.[3]): ;

Коэффициент упругого скольжения:

Отсюда действительное передаточное число:

;

Скорректируем частоту вращения и крутящий момент на 2-м валу:

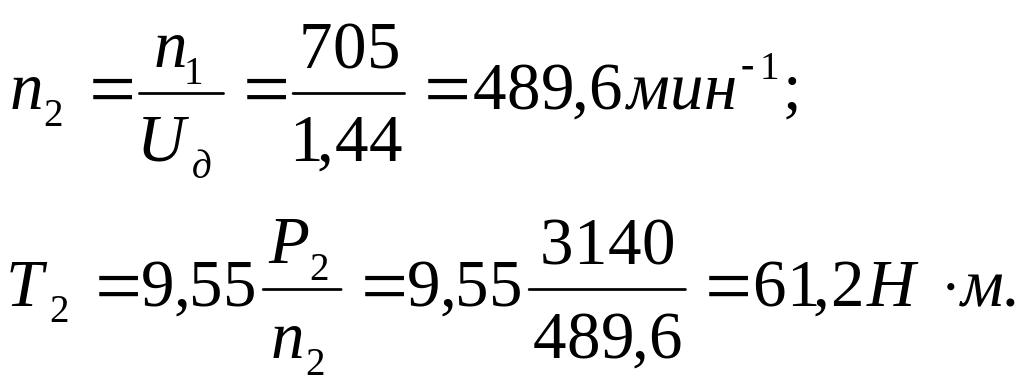
Найдём максимальное и минимальное межосевые расстояния:

Исходя из компоновки привода принимаем:

Расчётная длина ремня:

Действительная длина ремня по таблице 2.2.6.[3] ;

Уточняем межцентровое расстояние:

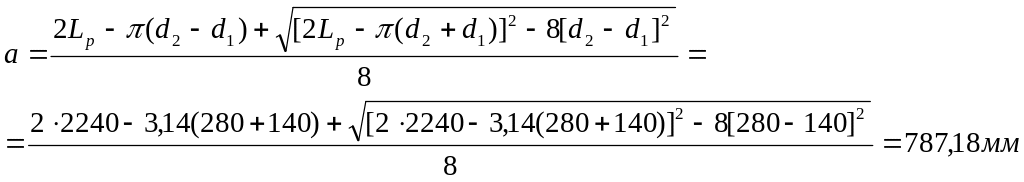
Угол обхвата ремнём меньшего шкива:

;

Скорость ремня:

Число ремней:

Принимаем Z=3;

Где (сечение ремня, ) – мощность передаваемая одним ремнём, кВт (табл.2.2.7.[3])

- коэффициент, учитывающий число ремней в передаче (табл. 2.2.5.[3]);

сечение ремня) (табл. 2.2.6.[3]);

- коэффициент, учитывающий динамичность нагружения передачи и режим её работы.

Сила, нагружающая валы передачи:

Н;

Окружное усилие:

Н;

Напряжения в ремне от действия центробежных сил:

МПа;

Наибольшее напряжения в ремне:

МПа; МПа;

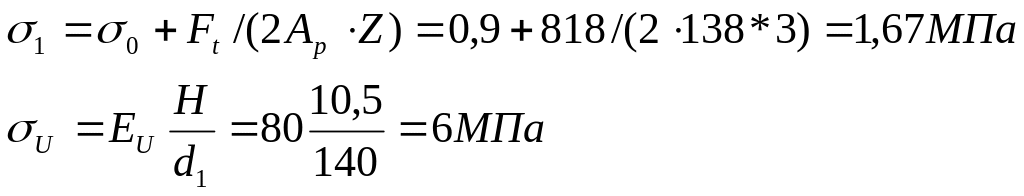
Допускаемое окружное усилие:

(табл.:3.7;3.8;3.9[15])

Число пробегов ремня:

Рассчитаем долговечность передачи:

;σ = σ1+σu+σц =2,487+6+0,0059=8,546 МПа;

σu=6 МПа; σц=0,059 МПа: σ 1=2,487 МПа; ν1=1.7; ν2=1;

L =(10 /7200i)( σ /σ ) * ν1 *ν2=(10/7200*3,14)*(9/8,546) *1,7*1=2046,6 часов;

2.3 Расчет редуктора

2.3.1. Расчет 1-й зубчатой цилиндрической передачи

Выбираем материалы со средними механическими характеристиками по табл. 16.2.1 [«Детали машин Проектирование» А.Т. Скойбеда]:

Для шестерни:

Сталь: 45ХН

Термическая обработка: улучшение

Твердость: НВ 275

Для зубчатого колеса:

Сталь: 35ХМ

Термическая обработка: улучшение

Твердость: НВ 241

Расчет допускаемых контактных напряжений при расчете на усталость:

Определяем число часов работы передачи за весь срок службы:

L =L *365*K *24*K =10*365*0,7*24*0,6=36792 часа

Определяем базовое число нагружений:

N =30(HB1) =30(275) =21,4*10 ≤120*10

N =30(HB2) =30(241) =15,75*10 ≤120*10

Расчетное число циклов нагружений:

N =60*ci*ni* L *(∑K *K )

N =60*1*480*36792(1 *0,7+0,7 *0,3)=8,507*10

N =60*1*83,965*36792(1 *0,7+0,7 *0,3)=1,48*10

т.к. N < N выбираем формулу для расчета коэффициента долговечности:

Z = =

Z = =0,8366 ≥ 0,75

Z = =0,873 ≥ 0,75

Предел контактной выносливости:

σ =2*НВi + 70, МПа – для улучшенных колес

σ =2*275+70=620 МПа

σ =2*241+70=552 МПа

Коэффициент контактной выносливости:

σ = (σ /S )0,9*Z

σ =(620/1,1)*0,9*0,8366=421,234 МПа

σ =(552/1,1)*0,9*0,8933=403,421 МПа

Допускаемые напряжения для передачи:

σ =min ( 0,45(σ + σ ); 1,25(σ ) )=min ( 0,45(421,234 +403,421); 1,25*403,421 ) =

= min( 374,7 МПа ; 504,8 МПа) => σ =374,6469 МПа

Допускаемые напряжения изгиба:

σ =1,75*НВ1=1,75*275=481,25 МПа

σ =1,75*НВ2=1,75*241=421,8 МПа

Базовый предел выносливости (изгибной):

σ = σ *Ya*Yz – для улучшенных колес

причем Ya=1; Yz=1(поковка)

σ = σ * Ya*Yz=490*1*1=481,25 МПа

σ = σ * Ya*Yz=455*1*1=421,8 МПа

Коэффициент запаса: SF1= SF2=1,7 и gF=6

Расчетное эквивалентное число циклов нагружений:

NFEi=60*ci*ni*Lh*(∑K *K )

NFE1=60*1*480*36792*(1 *0,7+0,7 *0,3)=7,78*10

NFE2=60*1*83,96*36792*(1 *0,7+0,7 *0,3)=1,36*10

NFlim=4*10

Коэффициент долговечности:

YNi= 1

Поскольку NFEi > NFlimi принимаем YN1=YN2=1

И определяем напряжения изгиба (при расчете на усталость):

σ = (σ / SFi)* YNi

σ =(481,25 МПа /1,7)*1=283,08 МПа

σ =(421,8 МПа /1,7)*1=248,1 МПа

Определение кинематических параметров передачи:

Определяем межосевое расстояние по формуле:

a_w  K_a*(u+1)*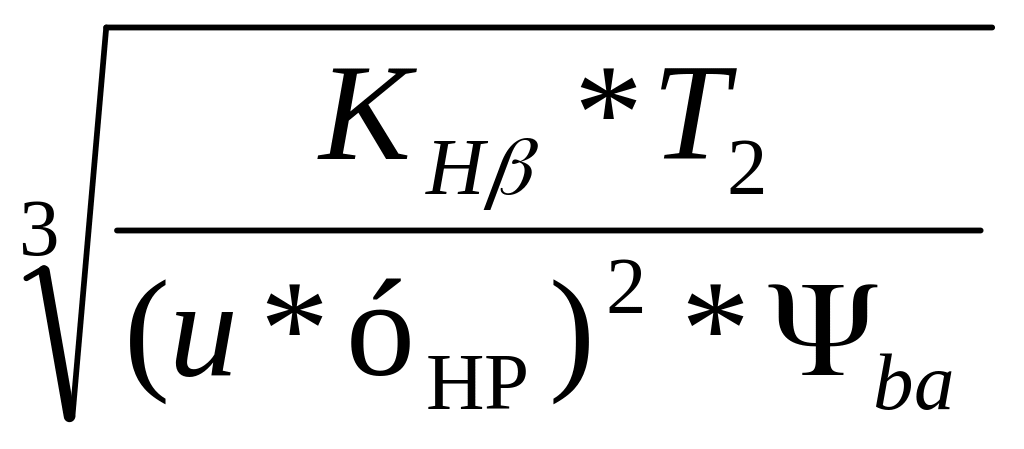 , мм

K_a = 430 - коэф. для стальных косозубых колес

u=5,66 – передаточное отношение

T2=573,60 Н*м – крутящий момент на втором валу

σ =374,64 МПа – допускаемое контактное напряжение

=0,5* *(u+1)=0,5*0,4*(5,6+1)=0,5985

по [ «Детали машин Проектирование» А.Т. Скойбеда] определяем коэффициент

K =1,1

a_w  430*(5,6+1)* =166,9 мм

по ГОСТу a_w = 160 мм

Определяем ширину зубчатого венца:

b = * a_w=0,4*160 =64 мм

принимаем b = 50 мм

b = b +4 = 64+4 = 68 мм

Определяем модуль зацепления:

mn =(0,015-0,03)* a_w = 0,015*160=2,4 мм

принимаем mn =2 мм

Определяем суммарное число зубьев и угол наклона зубьев:

Z∑=(2* a_w / mn)*cosβ` , β`=10°

Z∑=(2*160/ 2)*cos(10°)=158

следовательно Z∑=158

Определяем число зубьев меньшего (ведущего) колеса:

Z1= Z∑/(u+1)=158/(5,6+1) =24

Следовательно Z1=24

Z2= Z∑- Z1=158 – 24 = 134

уточняем передаточное отношение:

u = 134 / 24 = 5,58

Уточняем угол наклона зубьев:

cosβ= (Z∑* mn) / (2* a_w)=158*2/ 320 = 0,9875 , β=9,068°

Определяем геометрические параметры зубчатых колес:

начальные диаметры:

dw1= ( mn / cosβ )*Z1 = ( 2 / 0,9875 )*24 = 48,60 мм

dw2=( mn / cosβ )*Z2 = ( 2 / 0,9875 )*134 = 271,40 мм

уточняем межосевое расстояние:

a_w = (dw1+ dw2) / 2 = (48,60 +271,40) / 2 = 160 мм

Определяем диаметры вершин:

da1= dw1 + 2* mn =48,60 + 2*2 = 52,60мм

da2= dw2 + 2* mn = 271,40 + 2*2 =275,40 мм

Определяем диаметры впадин зубьев:

df1= dw1-2,5* mn =48,60 – 2,5*2 = 43,60мм

df2= dw2-2,5* mn =271,40 – 2,5*2 = 266,40мм

Определяем окружную скорость в зацеплении:

V = (π*d w1*n1) / (60*1000) = (3,14*48,60 *475,247) / (60*1000) = 1,2 м/с

в зависимости от окружной скорости выбираем степень точности = 9

Определяем усилия действующие в зацеплении:

окружная: Ft = (2*T1) / dw1 = (2*585,59) / (2*271,40*10 ) = 2,15 кН

радиальная: Fr = (Ft / cosβ)*tn(α ) = (2,15 / 0,9875)*0,364 = 0,795 кН

осевая: Fa = Ft*tnβ = 2,15*0,1596 = 0,3431 кН

. Выполняем проверочный расчет на контактную усталость:

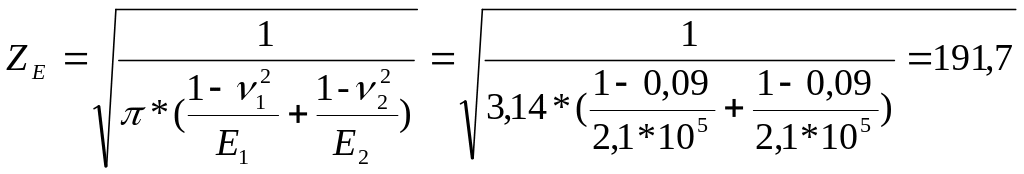- коэффициент учитывающий геометрию

коэффициент Пуассона (для стали 0,3)

E₁, E₂ – модуль продольной упругости материалов (2,1*10⁵)

- угол наклона зубьев ( )

- коэффициент торцового перекрытия

, где

=1

- взяли по графику (стр.111 [2]) для степени точности 8

(стр. 111 формула 6.9) [2]

(стр. 111 формула 6.10) [2]

(стр. 152 таблица 6.10) [2]

g_o=56 (стр. 152 таблица 6.11) [2]

=1,25*1,0169*1=1,27

МПа

МПа

- условие выполняется

. Выполняем проверочный расчет на изгибную усталость:

, где

(стр.114) [2]

(по графику рис. 6.14) [2]

Zv=Z1/cos =24/0.9875=24.92;

Yfs=3.9 Y =1/ =1/1.7012=0.5878; Y =1- =1-(1.606*9.068/120)=0.8786;

МПа

Zv2=134/0.9629=139.15; Yfs2=0.5878; Y =0.5878;Y =0.8786;

МПа

- условие выполняется