Задания к аттестационной работе

Задание 1 Программирование алгоритмов разветвляющейся структуры

Номер варианта выбирается по последней цифре номера зачётной книжки. Например, зачётная книжка № 931417  Вариант № 7

Варианты задания

0. Даны действительные числа x, y. Определить, принадлежит ли точка с координатами (x, y) заштрихованной области.

0. Даны действительные числа x, y. Определить, принадлежит ли точка с координатами (x, y) заштрихованной области.

0. Даны действительные числа x, y. Определить, принадлежит ли точка с координатами (x, y) заштрихованной области.

0. Даны действительные числа x, y. Определить, принадлежит ли точка с координатами (x, y) заштрихованной области.

0. Даны действительные числа x, y. Определить, принадлежит ли точка с координатами (x, y) заштрихованной области.

0. Даны действительные числа x, y. Определить, принадлежит ли точка с координатами (x, y) заштрихованной области.

0. Даны действительные числа x, y. Определить, принадлежит ли точка с координатами (x, y) заштрихованной области.

0. Даны действительные числа x, y. Определить, принадлежит ли точка с координатами (x, y) заштрихованной области.

0. Даны действительные числа x, y. Определить, принадлежит ли точка с координатами (x, y) заштрихованной области.

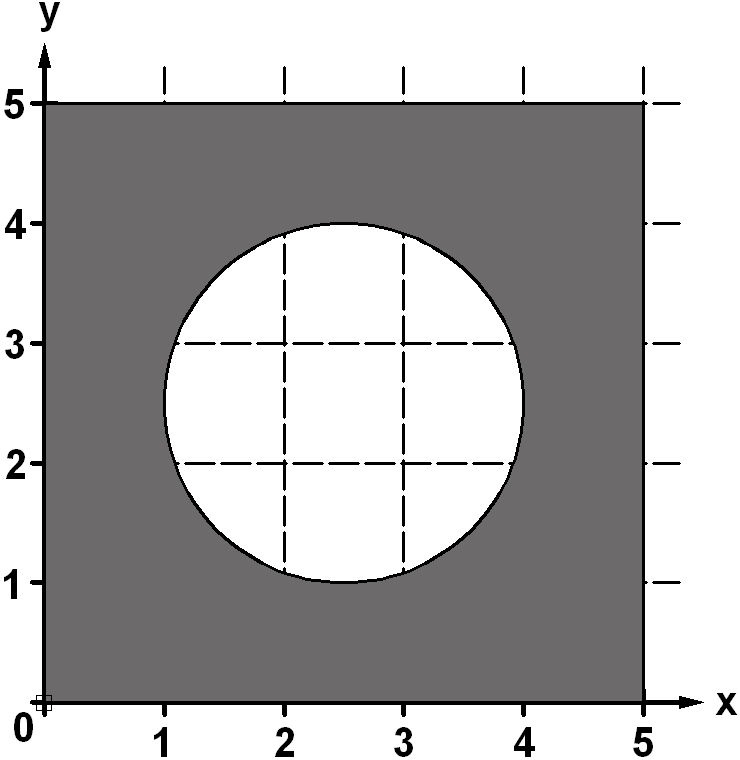
0. Даны действительные числа x, y. Определить, принадлежит ли точка с координатами (x, y) заштрихованной области.

Примечание: x, y вводятся с клавиатуры; на экран выводится соответствующее сообщение (“Точка принадлежит заштрихованной области”, “Точка не принадлежит заштрихованной области”). При решении задач нужно использовать уравнение окружности радиусом R; уравнение наклонной прямой , где – тангенс угла наклона этой прямой по отношению к оси абсцисс.

Задание 2 Программирование алгоритмов циклической структуры с внутренним разветвлением

Написать программу вычисления функции . Заполнить таблицу значений при с шагом .

Варианты заданий выбираются из таблицы 1. Номер варианта выбирается по сумме последних трёх цифр номера зачётной книжки. Например, зачётная книжка № 931417  Вариант № 4+1+7=12

Таблица 1

Варианты задания

№
0	– 2	2	0.25
1	– 0.9	0.9	0.1
2	– 1	3	0.2
3	2	4	0.2
4
5	– 4	0	0.4
6
7	4.2	5.85	0.15
8	– 3	6	0.5
9		0
10	– 2.1	3	0.3
11
12	– 20	20	4
13	12	13.2	0.1
14
15	– 0.1	0.1	0.02
16	0	1.4	0.1
17	– 5	5	1
18	– 2	2	0.25
19	– 1.4	1.4	0.2
20
21	– 1.05	1.05	0.15
22	0	2.4	0.15
23	– 12	0	1
24	3	7	0.25
25
26	1	3	0.25
27

Примечание: , и вводятся с клавиатуры (если эти величины в задании выражены через , то их следует предварительно рассчитать на калькуляторе и ввести с точностью до 7 знаков после запятой); вывод результатов на экран осуществляется в два столбика ( ) с точностью до 6 знаков после запятой.

Задание 3 Программирование алгоритмов с итерационными циклами

На интервале найти с точностью корни уравнения методом деления отрезка пополам.

Варианты заданий выбираются из таблицы 2. Номер варианта выбирается по сумме третьей, пятой и шестой цифр номера зачётной книжки. Например, зачётная книжка № 931417  Вариант № 1+1+7=9

Таблица 2

Варианты задания

№
0	– 5,5	– 4
1	0	1
2	5	10
3	1	3
4	1	6
5	– 3	1
6	0	3
7	0,2	1,4
8	0	2
9	– 3	0
10	7	11
11	0,1	0,6
12	1,5	1,7
13	4	7
14	– 3	– 2
15	5	7
16	– 4	– 1
17	2	4
18	0,6	1,4
19	1	2,2
20	– 1,5	1,5
21	– 2	1
22	– 3,5	– 1,5
23	0,8	4
24	6,4	7,7
25	– 10	0
26	2	5
27	1	2

Примечание: , и вводятся с клавиатуры; на экран осуществляется вывод промежуточных результатов в три столбика ( ), где – номер шага (целое число), – середина отрезка ; и выводятся с точностью до 6 знаков после запятой; когда и длина отрезка , и модуль становятся меньше , делается сообщение о завершении вычислений.

Задание 4 Программирование алгоритмов с итерационными циклами, содержащими вложенные арифметические циклы

Вычислить методом прямоугольников или трапеций (на выбор), где , , , , с точностью .

Варианты заданий выбираются из таблицы 3. Номер варианта выбирается по сумме последних двух цифр номера зачётной книжки. Например, зачётная книжка № 931417  Вариант № 1+7=8

Таблица 3

Варианты задания

№
0	5	10
1	1	2,5
2	– 3	1
3	0	3
4	– 3	2
5	0
6		0
7	1	7
8
9	0,5	3
10	0
11	– 4	– 1
12		0
13	0
14	4	10
15	0	1,5
16
17	3	6
18

Примечание: , , и вводятся с клавиатуры; в качестве первоначального значения числа разбиений выбирается ; на экран осуществляется вывод промежуточных результатов в четыре столбика ( ); в качестве исходного значения выбирается ноль; когда модуль становится меньше , делается сообщение о завершении вычислений, в противном случае удваивается, и вычисления повторяются.