
- •1. Требования к теоретической части курсовой работы
- •2.Методические рекомендации к выполнению статистических расчётов курсовых, контрольных и выпускных квалификационных работ
- •Тема 1. Предмет, метод и задачи статистики.
- •1.1. Предмет, методы, задачи статистики
- •1.2. Основные понятия статистической науки: стат. Совокупность, варьирующие признаки, стат. Закономерность, стат. Показатель.
- •Тема 2. Статистическое наблюдение. Абсолютные и относительные величины
- •2.1. Понятие стат. Наблюдения. Требования к собираемой информации.
- •2.2. Основные виды, формы и способы наблюдения.
- •2.3. Точность наблюдения и контроль данных наблюдения.
- •2.4. Абсолютные и относительные величины
- •Тема 3. Сводка и группировка статистических данных.
- •3.1. Статистическая сводка, ее содержание, задачи, роль в анализе информации
- •3.2. Группировка - основа статистической сводки. Виды группировки, их применение в статистике
- •Пример типологической группировки
- •Пример структурной группировки
- •1). Единицы группируются по факторному признаку, а не по результативному;
- •Техника проведения аналитической группировки.
- •Построение интервального ряда распределения банков по объему кредитных вложений
- •3.3. Статистические ряды распределения, их виды и характеристики
- •Пример атрибутивного ряда
- •Пример дискретного ряда распределения
- •3.4. Табличное и графическое представление статистических данных
- •Правила построения статистических таблиц:
- •3. Комбинационные таблицы - подлежащее содержит группировку единиц совокупности по двум или более признакам, взятым в сочетании. Графическое представление статистических данных
- •Полигон распределения частот
- •Гистограммы
- •Кумулята
- •Тема 4. Средние величины
- •4.1. Сущность средних величин. Две формы средних величин.
- •(4.1.1.) (Для несгруппированных данных)
- •(Для сгруппированных данных) (4.1.2.)
- •1. Алгебраическая сумма отклонений индивидуальных значений признака от средней арифметической равна нулю (так называемое "нулевое" свойство).
- •2. Сумма квадратов отклонений индивидуальных значений признака от средней арифметической есть число минимальное (так называемое "минимальное" свойство).
- •3. Если все варианты ряда распределения увеличить или уменьшить на одну и ту же величину или в одно и тоже число раз, то средняя увеличится или уменьшится на ту же величину, или в тоже число раз.
- •Пример расчета средней арифметической простой
- •Пример расчета средней арифметической взвешенной
- •4.3. Средняя гармоническая.
- •4.4. Структурные средние (Мода, Медиана)
- •Пример нахождения Моды в дискретном ряду распределения
- •Тема 5 Статистическое изучение вариации
- •5.1.Понятие вариации. Основные показатели вариации
- •5.2. Правило сложения дисперсий и его применение.
- •5.3. Характеристика формы распределения. (самостоятельно!)
- •5.1. Понятие вариации. Основные показатели вариации
- •4. Среднее квадратическое отклонение (σ) – корень из среднего квадрата отклонений вариантов признака от средней арифметической величины признака. Сохраняет размерность изучаемого признака.
- •Относительные показатели вариации
- •1. Коэффициент вариации (Vσ) – относительный показатель вариации, который определяется как отношение среднего квадратического отклонения и арифметической средней изучаемого показателя.
- •2. Показатель осцилляции: ; (5.1.12.)
- •3. Линейный коэффициент вариации: . (5.1.13)
- •5.2.Правило сложения дисперсий и его применение
- •1)Объема кредитных вложений (наш факторный признак - х);
- •2)Прочих, неучтенных факторов.
- •1)Объема кредитных вложений (наш факторный признак - х);
- •1)Прочих, неучтенных факторов.
- •3. Расчёт внутригрупповых дисперсий ( ) и средней из них ( ).
- •5.3.Характеристика формы распределения
- •А число е ≈ 2,71828 – основание натуральных логарифмов.
- •1. Кривая имеет форму колокола.
- •4. Кривая имеет две точки перегиба при , находящиеся на расстоянии от (среднего квадратического отклонения)
- •6. В промежутке находится 68,3% всех значений признака.
- •(Правило трёх ).
- •Тема 6. Метод выборочного наблюдения
- •6.1.Понятие о выборочном наблюдении и ошибках выборки
- •6.2.Способы формирования выборочной совокупности
- •6.3 Средняя и предельная ошибки выборки
- •1. Определение ошибки выборки для среднего объема кредитных вложений банков и границ, в которых будет находиться генеральная средняя
- •_________?% _______?% (Проценты)
- •6.4.Определение необходимого объема выборки Определение необходимого объема выборки с заданным значением допустимой предельной ошибки выборки, равной 10 млн. Руб.
- •Тема 7. Корреляционно – регрессионный анализ социально-экономических явлений
- •7.1. Понятие о корреляционной связи. Виды и формы корреляционных связей
- •Если ни один обобщающий параметр не меняется систематически, то статистической связи нет!
- •7.2.Корреляционный метод анализа взаимосвязи
- •4. Метод аналитической группировки.
- •7.3.Регрессионный метод анализа взаимосвязи
- •7.4. Пример построения однофакторной регрессионной модели связи
- •Тема 8. Ряды динамики
- •8.1. Понятие и классификация рядов динамики. Сопоставимость уровней и смыкание рядов динамики
- •Способ выражения уровней ряда
- •Способ представления хронологии в рядах динамики
- •Пример интервального ряда динамики
- •Пример моментного ряда динамики
- •Расстояние между периодами или датами в рядах динамики
- •8.2. Аналитические показатели изменения уровней ряда динамики
- •8.3. Средние показатели в рядах динамики
- •, (8.3.8.) Когда отсутствует перелом в тенденции
- •8.4. Экстраполяция прогнозов в рядах динамики
- •Прогнозирование объемов реализации продукции с использованием среднего темпа роста
- •8.5. Методы выявления сезонных колебаний
- •8.6. Методы анализа основной тенденции в рядах динамики
- •Производство зерна в рф, млн.Тонн
- •Тема 9. Экономические индексы
- •9.1. Понятие о статистических индексах. Виды и классификация индексов.
- •Индексируемый показатель – показатель, уровни которого сравниваются. Например, цена , количество продаж , объем товарооборота ;
- •Сравниваемый уровень показателя – уровень показателя, который сравнивают с другим, его называют отчетным или текущим , ;
- •Базисный уровень показателя – уровень, с которым происходит сравнение , ;
- •9.2. Индивидуальные и общие индексы. Проблемы соизмерения индексируемых величин в агрегатных индексах.
- •1) Что включить в один индекс, какие элементы объединяются в одном индексе?
- •2) Необходимо правильно выбрать соизмеритель или вес, т.Е. Постоянный признак. Выбор веса зависит от того, какой признак исследуется – количественный или качественный.
- •9.3. Индексы средние из индивидуальных
- •9.4. Взаимосвязь индексов. Индексный метод выявления влияния роли отдельных факторов. Все три индекса
- •9.5. Индексы постоянного и переменного состава. Индексы фиксированной структуры.
- •3. Средний темп роста ( ) –
3.3. Статистические ряды распределения, их виды и характеристики
Результаты сводки могут быть представлены в виде статистических рядов распределения.
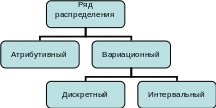
Схема 3.3.1. Виды рядов распределения
Статистическим рядом распределения называют упорядоченное распределение единиц совокупности на группы по изучаемому признаку.
В зависимости от вида признака, рассматриваемого как группировочный ряды могут быть вариационными (количественными) и атрибутивными (качественными).
Атрибутивные признаки — это признаки, не имеющие количественной меры. Например, пол (мужской, женский), вид экономической деятельности, вид продукции, профессия рабочего и т.д.
Количественные признаки — это признаки, имеющие количественное выражение у отдельных единиц совокупности, например, заработная плата рабочих, стоимость продукции промышленных предприятий, возраст людей, урожайность отдельных участков посевной площади и т.д.
Пример атрибутивного ряда
Табл.3.3.1.
Распределение студентов по полу в группе 320
№п/п |
Пол студентов,
(
|
Число студентов, чел. ( )
|
Число студентов в % к итогу, частость ( |
Число студентов в долях к итогу, частость ( |
1 |
2 |
3 |
4 |
|
1 |
женский |
28 |
? |
? |
2 |
мужской |
7 |
? |
? |
Итого: |
|
35 |
? |
? |
Вариационный ряд – ряд, построенный по количественному признаку, причем значения признака располагаются в порядке возрастания или в порядке убывания

Схема 3.3.2 Элементы ряда распределения
Варианта
(а) – (![]() )
значения
группировочного признака в вариационном
ряду распределения (в нашем случае –
объем кредитных вложений, млн.руб.).
)
значения
группировочного признака в вариационном
ряду распределения (в нашем случае –
объем кредитных вложений, млн.руб.).
Частота
(![]() )
– абсолютное значение случаев данного
варианта, т.е. то число раз, сколько
встречается элемент в статистической
совокупности (т.е. в нашем случае - то
число банков, которое встречается в
совокупности в том или ином интервале).
)
– абсолютное значение случаев данного
варианта, т.е. то число раз, сколько
встречается элемент в статистической
совокупности (т.е. в нашем случае - то
число банков, которое встречается в
совокупности в том или ином интервале).
Частость – ( ) - относительная доля каждой частоты в общей сумме частот, выраженнная в процентах или долях единицы (в нашем случае - тот процент (%) или доля банков, которое встречается в совокупности в том или ином интервале).
Вариационные ряды могут быть дискретными или интервальными.
Дискретный ряд
распределения
— это ряд, в котором варианты (![]() )выражены
целым
числом.
)выражены
целым
числом.
Пример дискретного ряда распределения
Таблица 3.3.2.
Распределение рабочих N–го цеха по разрядам
Тарифный разряд ( ) |
Число рабочих, чел.
|
1-й |
10 |
2-й |
20 |
3-й |
40 |
4-й |
60 |
5-й |
50 |
6-й |
20 |
Итого: |
200 |
Интервальный ряд распределения — это ряд, в котором значения признака заданы в виде интервала.
В интервальных рядах признак может меняться непрерывно от min до max значения, причем отличаться может друг от друга на сколь угодно малую величину.
Интервальный ряд применяется в тех случаях, если значения признака меняются непрерывно, а также если дискретный признак меняется в очень широких пределах, т.е. число вариантов ( ) достаточно велико.
Правило построения рядов распределения, выбор количества групп и величины интервалов такое же, как и при группировке.
На основе групповых итоговых строк «Всего» табл. 3.2.6. формируется таблица 3.3.3., представляющая интервальный ряд распределения банков по объему кредитных вложений.
Таблица 3.3.3.
Распределение банков по объему кредитных вложений
|
Номер группы |
Группы банков по объему кредитных вложений, млн. руб.,
|
Число банков,
|
П О Д Л Е Ж А Щ Е Е |
СКАЗУЕМОЕ |
||
1 |
375,00 - 459,00 |
4 |
|
2 |
459,00 - 543,00 |
5 |
|
3 |
543,00 - 627,00 |
11 |
|
4 |
627,00 - 711,00 |
7 |
|
5 |
711,00 - 795,00 |
3 |
|
|
Итого |
30 |
|
Помимо частот групп в абсолютном выражении в анализе интервальных рядов используются ещё характеристики ряда, приведенные в графах табл. 3.3.4.:
Кумулятивные частоты групп в относительном выражении, накопленные (кумулятивные) частоты
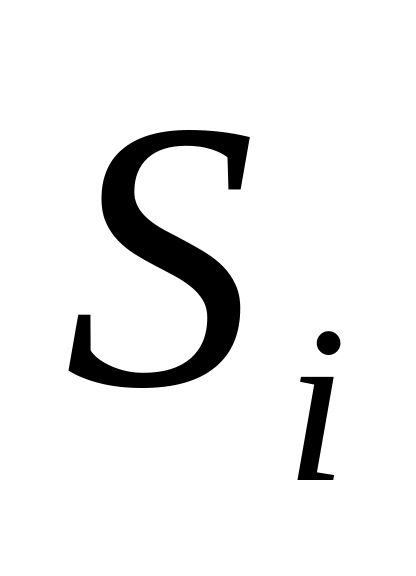 получаемые
путем последовательного суммирования
частот всех предшествующих (i-1)
интервалов.
получаемые
путем последовательного суммирования
частот всех предшествующих (i-1)
интервалов.накопленные частости, рассчитываемые по формуле
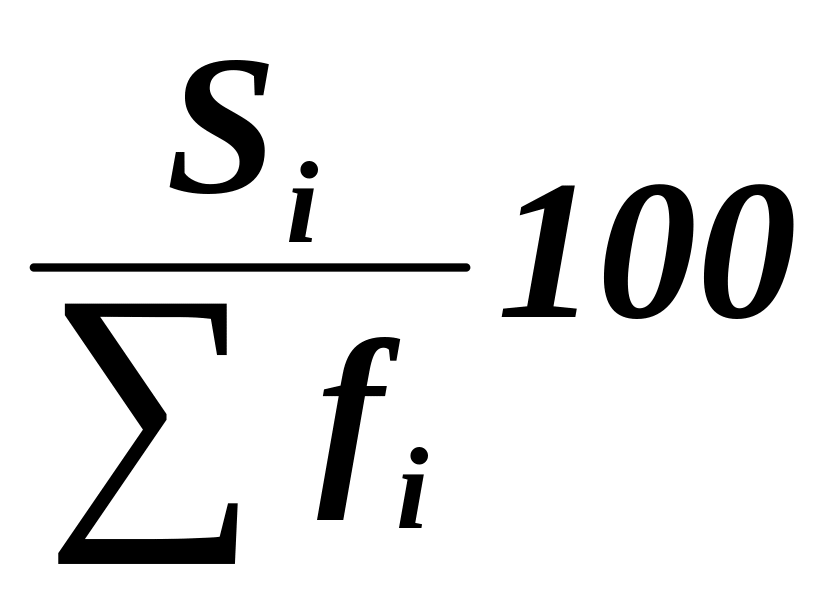 .
(гр. 6 табл. 3.3.4.)
.
(гр. 6 табл. 3.3.4.)
Построим ряд распределения для сквозной задачи по признаку «Величина кредитных вложений»
Ряд распределения банков по величине кредитных вложений |
Таблица 3.3.4.
|
|
|||
№ группы |
Группа банков по величине кредитных вложений, млн. руб.
|
Число банков, |
Накоплен-ная |
Накоплен-ная частость, %
|
|
в абсолют-ном выраже-нии |
в % |
частота
|
|||
1 |
2 |
3 |
4 |
5 |
6 |
1 |
375,00 - 459,00 |
4 |
13,3 |
4 |
13,3 |
2 |
459,00 - 543,00 |
5 |
16,7 |
? |
? |
3 |
543,00 - 627,00 |
11 |
36,7 |
? |
? |
4 |
627,00 - 711,00 |
7 |
23,3 |
? |
? |
5 |
711,00 - 795,00 |
3 |
10,0 |
? |
? |
|
Итого |
30 |
100,0 |
? |
? |
![]()
Аналогично рассчитывается и частость, в т.ч. и накопленная
Сумма частот составляет объём ряда распределения (или объём статистической совокупности – суть одно и то же).
![]() ,
,
![]() (3.3.1)
(3.3.1)
В
нашем случае
![]()
где: i – порядковый номер группы в ряду распределения;
k – число групп в ряду распределения.
Объём
признака для вариационного ряда
распределения
будет определяться как
![]()
Ряд распределения может быть дополнен частостями (w) – частотами, выраженными в виде относительных величин структуры – коэффициентах (долях единицы) или процентах.
Сумма частостей равна 1 (или 100%):
![]() (3.3.2.)
(3.3.2.)
Вывод. Анализ интервального ряда распределения изучаемой совокупности банков показывает, что распределение банков по объему кредитных вложений ______является равномерным: преобладают банки с объемом кредитных вложений от____________________________. (это ____ банков, доля которых составляет______________); ________? банков (или ___%) имеют кредитные вложения менее 543,0 млн. руб., а _____? банков (____?%) – менее 711 млн. руб.
Статистические ряды распределения позволяют систематизировать и обобщать статистический материал. Однако они не дают всесторонней характеристики выделенных групп. Чтобы решить ряд конкретных задач, выявить особенности в развитии явления, обнаружить тенденции, установить зависимости, необходимо произвести группировку статистических данных. (см. выше.)
