1)Прочих, неучтенных факторов.

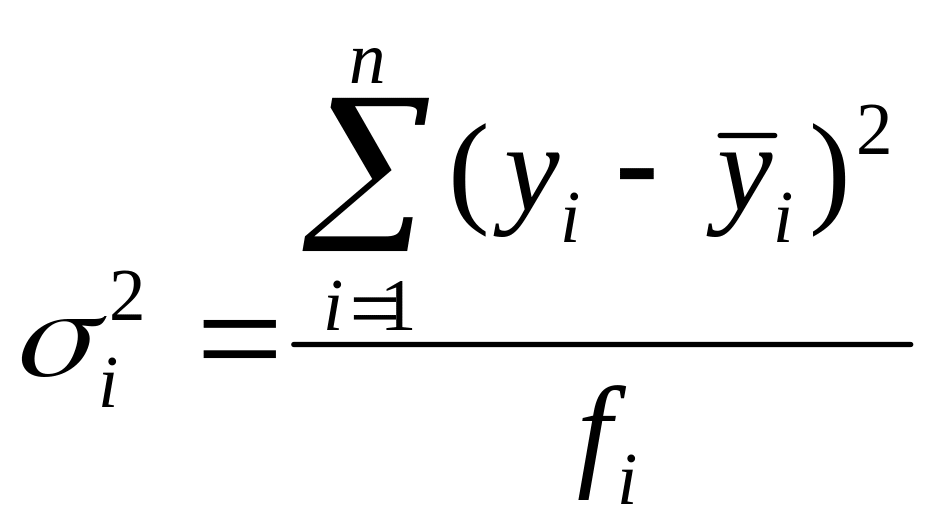(5.2.9.)

Средняя из внутригрупповых дисперсий ( ):

(5.2.10.)

3. Расчёт внутригрупповых дисперсий ( ) и средней из них ( ).

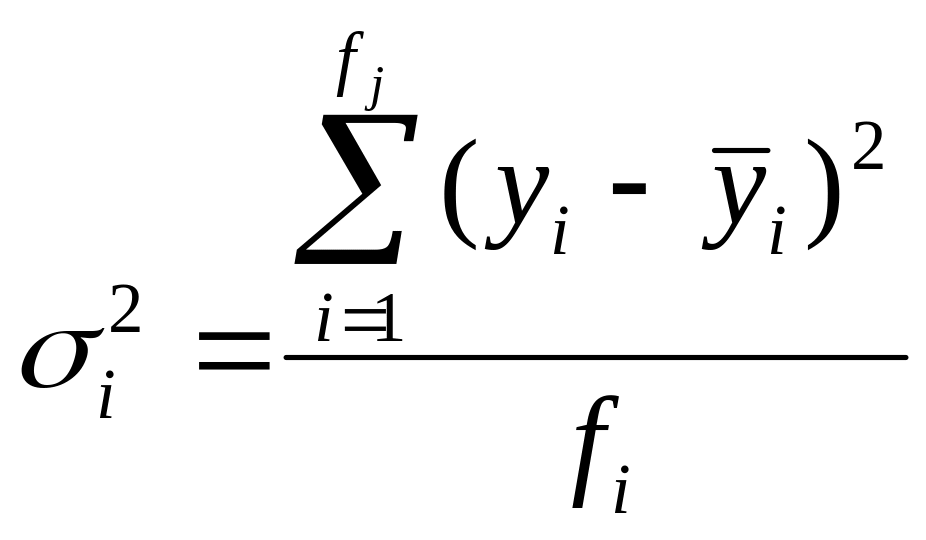
(5.2.11)

Для расчета внутригрупповой дисперсии составим вспомогательную таблицу:

Таблица 5.2.5.

Вспомогательная таблица для расчета внутригрупповой дисперсии

Номер группы	Группы банков по величине кредитных вложений, млн. руб.	Число банков, f	Прибыль банков, млн. руб.
			Значения прибыли банков в группе	Всего по группе	В среднем по группе на 1 банк
1	2	3	4	5	6=5:3
1	375,00 - 459,00	4	150,158, 168,208	684,000	171,000
2	459,00 - 543,00	5	195,213, 215,169, 210	1002,000	200,400
3	543,00 - 627,00	11	221,218, 191,214,230,239,236,237,256,228,238	2508,00	228,000
4	627,00 - 711,00	7	265,227,254,252,245,251,278	1772,00	253,143
5	711,00 - 795,00	3	288,293,303	884,00	294,667
	итого	30		6850,00	228,333

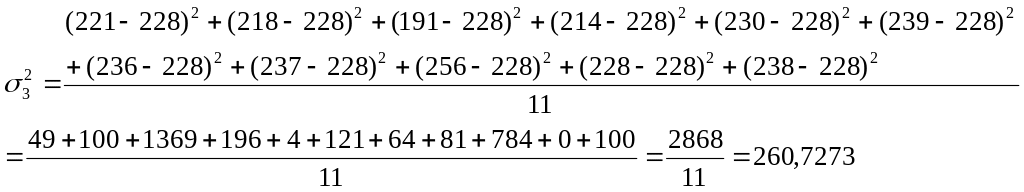
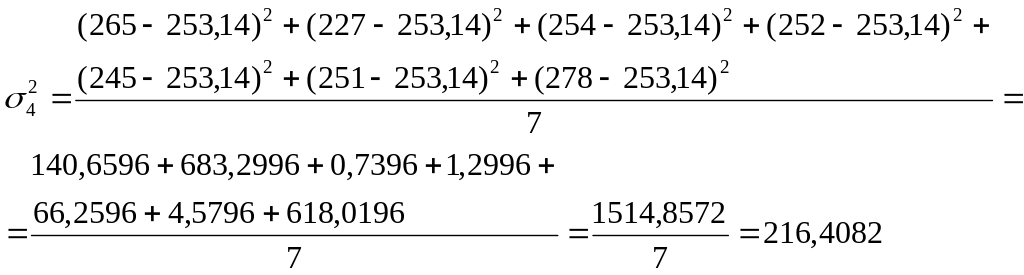
Средняя из внутригрупповых дисперсий :

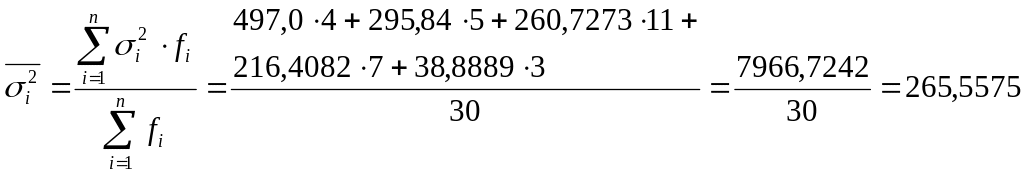
Проверим правило сложения дисперсий: общая дисперсия признака (σ²) равна сумме межгрупповой дисперсии (δ²) и средней из внутригрупповых дисперсий ( )

σ² = δ² +

1417,708=1152,019+265,6

5.3.Характеристика формы распределения

См. Метод. Указания к лаб. Работе №2 стр. 30-33

Форма распределения признака в вариационных рядах распределения отражает закономерность изменения частот с ростом значений варьируемого признака.

Приблизительное представление о форме распределения дают графики распределения: полигон и гистограмма.

Обобщающие характеристики формы распределения получают, используя кривые распределения.

Кривые распределения бывают эмпирические и теоретические.

Эмпирическая кривая распределения – это фактическая кривая распределения, построенная по данным наблюдения, которая отражает как общие, так и случайные условия, определяющие распределение признака.

Теоретическая кривая распределения – это кривая распределения, выражающая функциональную связь между варьирующим признаком и частотами.

Анализировать эмпирическую кривую, на изменение которой повлияли в том числе и случайные условия, – довольно трудно. Поэтому исследователи переходят к теоретической кривой распределения, по характеру распределения наиболее приближённой к первой. Теоретическая кривая признана отражать основную закономерность распределения признака при полном погашении случайных причин.

При выравнивании (аппроксимации) эмпирических вариационных рядов перед исследователем стоят три задачи:

1. Выяснение общего характера распределения.

2. Непосредственное выравнивание эмпирического распределения – замена эмпирической кривой на теоретическую.

3. Проверка соответствия найденного теоретического распределения эмпирическому.

Если мы посмотрим на характер изменения частот при изменении варьирующего признака в наших вариационных рядах распределения банков по величине кредитных вложений и по прибыли, то мы можем увидеть определённую закономерность. При росте варьирующего признака в наших вариационных рядах частоты сначала растут, затем, достигнув максимального значения, начинают снижаться. Такое распределение характерно для нормального распределения. Поэтому в качестве идеального распределения в наших случаях мы можем взять нормальное распределение. Кривая нормального распределения будет для нас теоретической кривой.

Кривая нормального распределения является наиболее распространённая формой распределения, по которой выравнивают эмпирическую кривую.

Кривая нормального распределения выражается стандартным уравнением нормальной кривой:

, (5.3.1.)

где: t = – нормированные отклонения (5.3.2.)