7.4. Примерные вопросы на защите работы
Что такое интерполяция?
Что такое узлы интерполяции?
В чем заключается задача отыскания интерполирующего многочлена?
Как построить интерполяционный многочлен Лагранжа?
Как определить погрешность метода интерполяции с помощью формулы Лагранжа?
Как образуются разделенные разности?
Как связаны разделенные разности и производная?
Что такое сплайн? Как происходит процесс интерполирования сплайнами?
Что такое конечная разность первого порядка? Как она находится?
Что такое конечная разность второго порядка? Как она находится?
Что такое конечная разность n-го порядка? Как она находится?
Первая интерполяционная формула Ньютона для равноотстоящих узлов.
Вторая интерполяционная формула Ньютона для равноотстоящих узлов.
Как находится погрешность метода интерполирования с помощью формул Ньютона?
15. Что значит «интерполирование вперед», «интерполирование назад»?
7.5. Задание
Построить интерполяционный многочлен методом неопределенных коэффициентов.
Построить график интерполяционной функции.
Найти приближенные значения функции при данных промежуточных значениях аргумента.
Найти приближенные значения функции при данных промежуточных значениях аргумента с помощью кубического сплайна и визуализируйте результаты сплайн-интерполяции.
Варианты заданий.
1 |
2 |
3 |
|||
x |
y |
x |
y |
x |
y |
1,415 |
0,8886 |
0,101 |
1,2618 |
0,15 |
0,8607 |
1,420 |
0,8900 |
0,106 |
1,2764 |
0,20 |
0,8187 |
1,425 |
0,8906 |
0,111 |
1,2912 |
0,25 |
0,7788 |
1,430 |
0,8917 |
0,116 |
1,3061 |
0,30 |
0,7408 |
1,435 |
0,8927 |
0,121 |
0,3213 |
0,35 |
0,7046 |
1,440 |
0,8940 |
0,126 |
1,3366 |
0,40 |
0,6703 |
1,445 |
0,8947 |
0,131 |
1,3521 |
0,45 |
0,6376 |
1,450 |
0,8957 |
0,136 |
1,3677 |
0,50 |
0,6065 |
1,455 |
0,8967 |
0,141 |
1,3836 |
0,55 |
0,5769 |
1,460 |
0,8977 |
0,146 |
1,3995 |
0,60 |
0,5488 |
1,465 |
0,8986 |
0,151 |
1,4157 |
0,65 |
0,5220 |
в точке x=1,4161 |
в точке x=0,1026 |
в точке x=0,7250 |
|||
4 |
5 |
6 |
|||
x |
y |
x |
y |
x |
y |
0,180 |
5,6154 |
3,50 |
33,115 |
0,115 |
8,6572 |
0,185 |
5,4669 |
3,55 |
34,813 |
0,120 |
8,2932 |
0,190 |
5,3263 |
3,60 |
36,598 |
0,125 |
7,9582 |
0,195 |
5,1930 |
3,65 |
38,474 |
0,130 |
7,6489 |
0,200 |
5,0664 |
3,70 |
40,447 |
0,135 |
7,3623 |
0,205 |
4,9461 |
3,75 |
42,521 |
0,140 |
7,0961 |
0,210 |
4,8317 |
3,80 |
44,701 |
0,145 |
6,8481 |
0,215 |
4,7226 |
3,85 |
46,993 |
0,150 |
6,6165 |
0,220 |
4,6185 |
3,90 |
49,402 |
0,155 |
6,3998 |
0,225 |
4,5191 |
3,95 |
51,935 |
0,160 |
6,1965 |
0,230 |
4,4242 |
4,00 |
54,598 |
0,165 |
6,0055 |
в точке x=0,175 |
в точке x=3,475 |
в точке x=0,1745 |
|||
7 |
8 |
9 |
|||
x |
y |
x |
y |
x |
y |
1,340 |
4,2556 |
0,01 |
0,9918 |
0,15 |
4,481 |
1,345 |
4,3532 |
0,06 |
0,9519 |
0,16 |
4,953 |
1,350 |
4,4552 |
0,11 |
0,9136 |
0,17 |
5,473 |
1,355 |
4,5618 |
0,16 |
0,8769 |
0,18 |
6,049 |
1,360 |
4,6734 |
0,21 |
0,8416 |
0,19 |
6,685 |
1,365 |
4,7903 |
0,26 |
0,8077 |
0,20 |
7,389 |
1,370 |
4,9130 |
0,31 |
0,7753 |
0,21 |
8,166 |
1,375 |
5,0419 |
0,36 |
0,7441 |
0,22 |
9,025 |
1,380 |
5,1774 |
0,41 |
0,7141 |
0,23 |
9,974 |
1,385 |
5,3201 |
0,46 |
0,6854 |
0,24 |
11,023 |
1,390 |
5,4706 |
0,51 |
0,6579 |
0,25 |
12,182 |
в точке x=1,3921 |
в точке x=0,492 |
в точке x=0,2444 |
|||
10 |
11 |
12 |
|||
x |
y |
x |
y |
x |
y |
0,45 |
20,194 |
1,345 |
4,3532 |
0,130 |
7,6489 |
0,46 |
19,613 |
1,350 |
4,4552 |
0,135 |
7,3623 |
0,47 |
18,942 |
1,355 |
4,5618 |
0,140 |
7,0961 |
0,48 |
18,174 |
1,360 |
4,6734 |
0,145 |
6,8481 |
0,49 |
17,301 |
1,365 |
4,7903 |
0,150 |
6,6165 |
0,50 |
16,312 |
1,370 |
4,9130 |
0,155 |
6,3998 |
0,51 |
15,198 |
1,375 |
5,0419 |
0,160 |
6,1965 |
0,52 |
13,948 |
1,380 |
5,1774 |
0,165 |
6,0055 |
0,53 |
12,550 |
1,385 |
5,3201 |
0,170 |
5,8255 |
0,54 |
10,993 |
1,390 |
5,4706 |
0,175 |
5,6558 |
0,55 |
9,264 |
1,395 |
5,6296 |
0,180 |
5,4954 |
в точке x=0,445 |
в точке x=1,374 |
в точке x=0,158 |
|||
РАБОТА №8
ЧИСЛЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ
8.1. ЦЕЛЬ РАБОТЫ
Сформировать у студентов представления о численном дифференцировании, привить умения составлять и применять формулы численного дифференцирования, оценивать их погрешности, дать навыки в использовании программных средств для проверки полученных результатов.
8.2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Изучить теоретическую часть. Выполните задания, соответствующие номеру Вашего варианта, и продемонстрируйте их преподавателю.
2. Оформите отчет по лабораторной работе, который должен содержать:
титульный лист;
исходные данные варианта;
решение задачи;
результаты решения задачи.
8.3. МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
Пример 8.1.
Рассмотрим функцию f(x), заданную таблично:
х |
у |
0,43 |
1,6359 |
0,48 |
1,7323 |
0,55 |
1,8768 |
0,62 |
2,0304 |
0,7 |
2,2284 |
0,75 |
2,3597 |
Интерполяционный многочлен имеет вид:
Вычислим значения
производной этой функции на отрезке
[0,43; 0,75]:
>> dx=0.01;
>> x=0.43:dx:0.75;
>> yf=-154.9063*x.^5+444.9904*x.^4-511.6367*x.^3+291.7494*x.^2-80.6863*x+10.099;
>> N=length(x);
>> m=1:N-1;
>> df(m)=(yf(m+1)-yf(m))/dx;
>> plot(df)
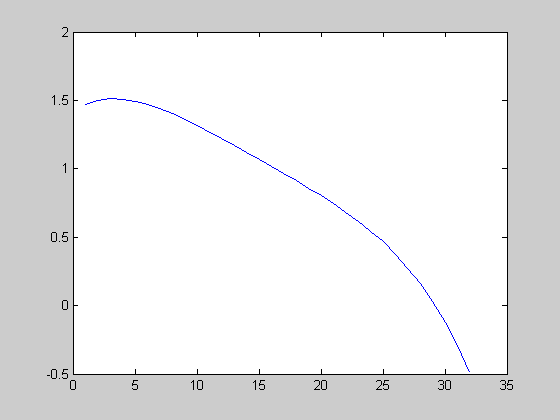
Рис. 8.1. График производной функции.