
- •С т а т и к а корабля модуль 5.5
- •3. Остойчивость
- •3.1. Общее понятие об остойчивости
- •3.2. Малые равнообъемные наклонения. Теорема Эйлера
- •3.3. Перемещение центра величины при малом равнообъемном наклонении
- •3.4. Метацентры и метацентрические радиусы
- •3.5. Восстанавливающий момент. Метацентрические формулы остойчивости
- •3.6. Приближенные формулы для вычисления некоторых элементов плавучести и начальной остойчивости
3.5. Восстанавливающий момент. Метацентрические формулы остойчивости
При
равнообъемном наклонении ЦТ
судна не меняет своего положения ,а ЦВ
перемещается в сторону наклонения. Вес
судна D
и сила поддержания ρgV
образуют
пару (рис. 6). Плечо этой пары
![]() называется плечом статической
остойчивости. Его величину можно
определить из
называется плечом статической
остойчивости. Его величину можно
определить из
![]() :
:
![]() .
Для малых углов
.
Для малых углов
![]() Восстанавливающий момент получится
равным
Восстанавливающий момент получится
равным
![]() .
(13)
.
(13)
Величина
![]() обозначается
обозначается
![]() и называется поперечной метацентрической
высотой.
и называется поперечной метацентрической
высотой.
Таким образом, поперечная метацентрическая высота – это возвышение метацентра М над центром тяжести G. Формулу (13) можно переписать в виде
![]() (13а)
(13а)
Для
наклонения около поперечной оси также
существует продольная метацентрическая
высота (рис.7)
![]() .
.
Тогда продольный восстанавливающий момент запишется в виде
![]() .
(14)
.
(14)
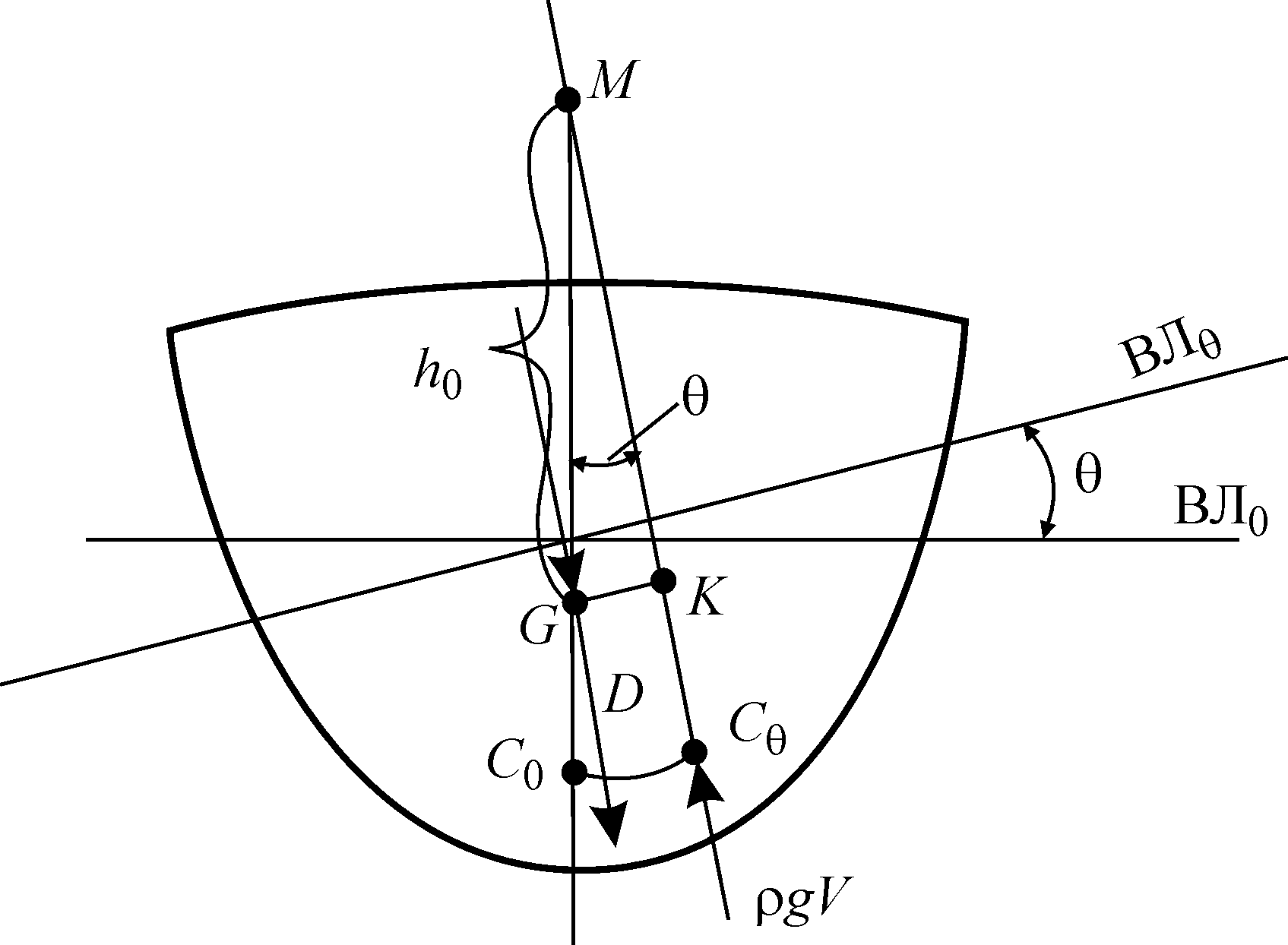
Рис.6 Поперечная метацентрическая высота
Формулы (13 а) и (14) называются метацентрическими формулами остойчивости.
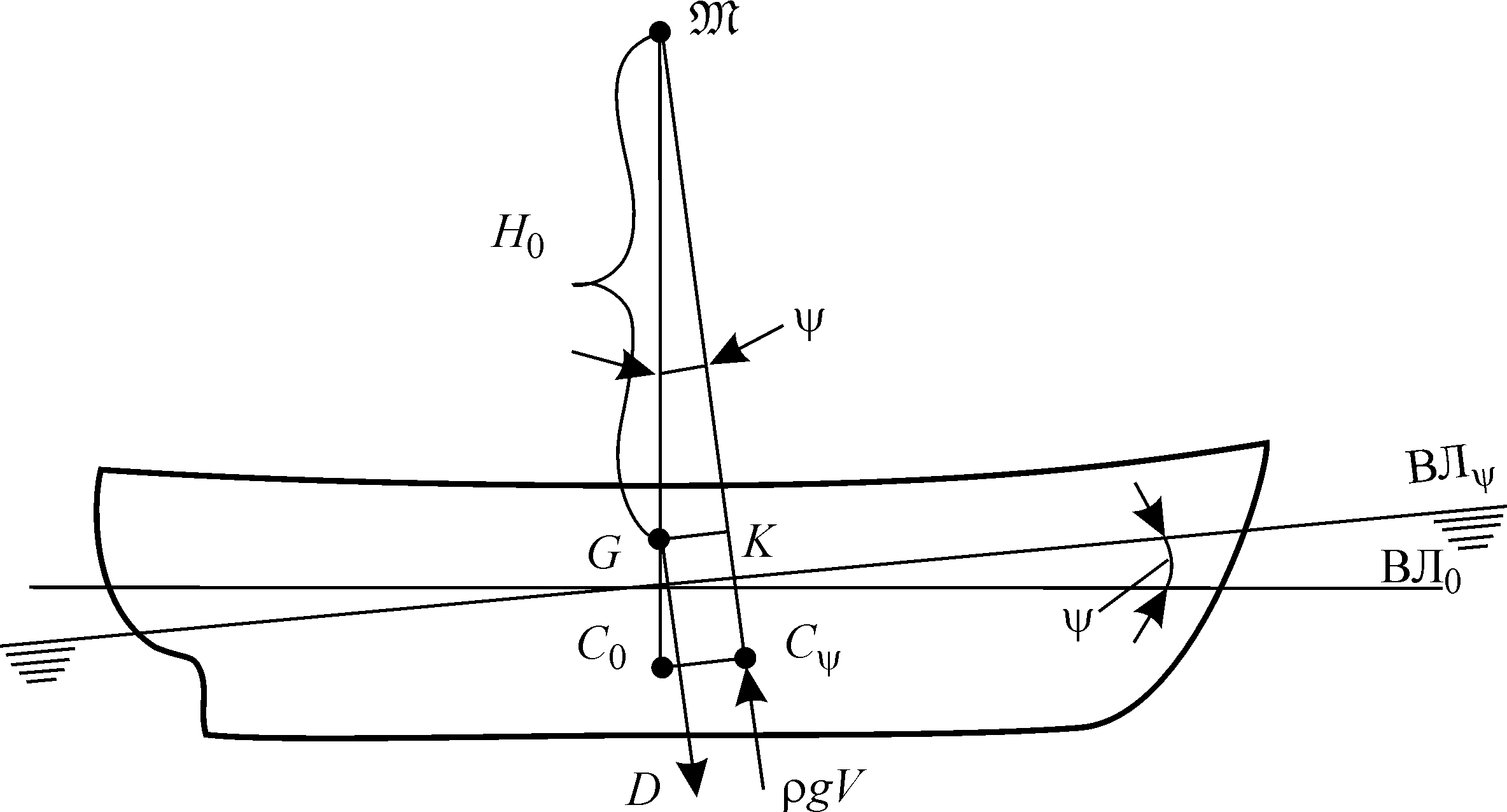
Рис.7 Продольная метацентрическая высота
Составим
выражения для определения
и
![]() .
Из рис.8 следует, что
.
Из рис.8 следует, что
![]() ;
(15)
;
(15)
![]() ;
(16)
;
(16)
![]() ;
(17)
;
(17)
![]() .
(18)
.
(18)
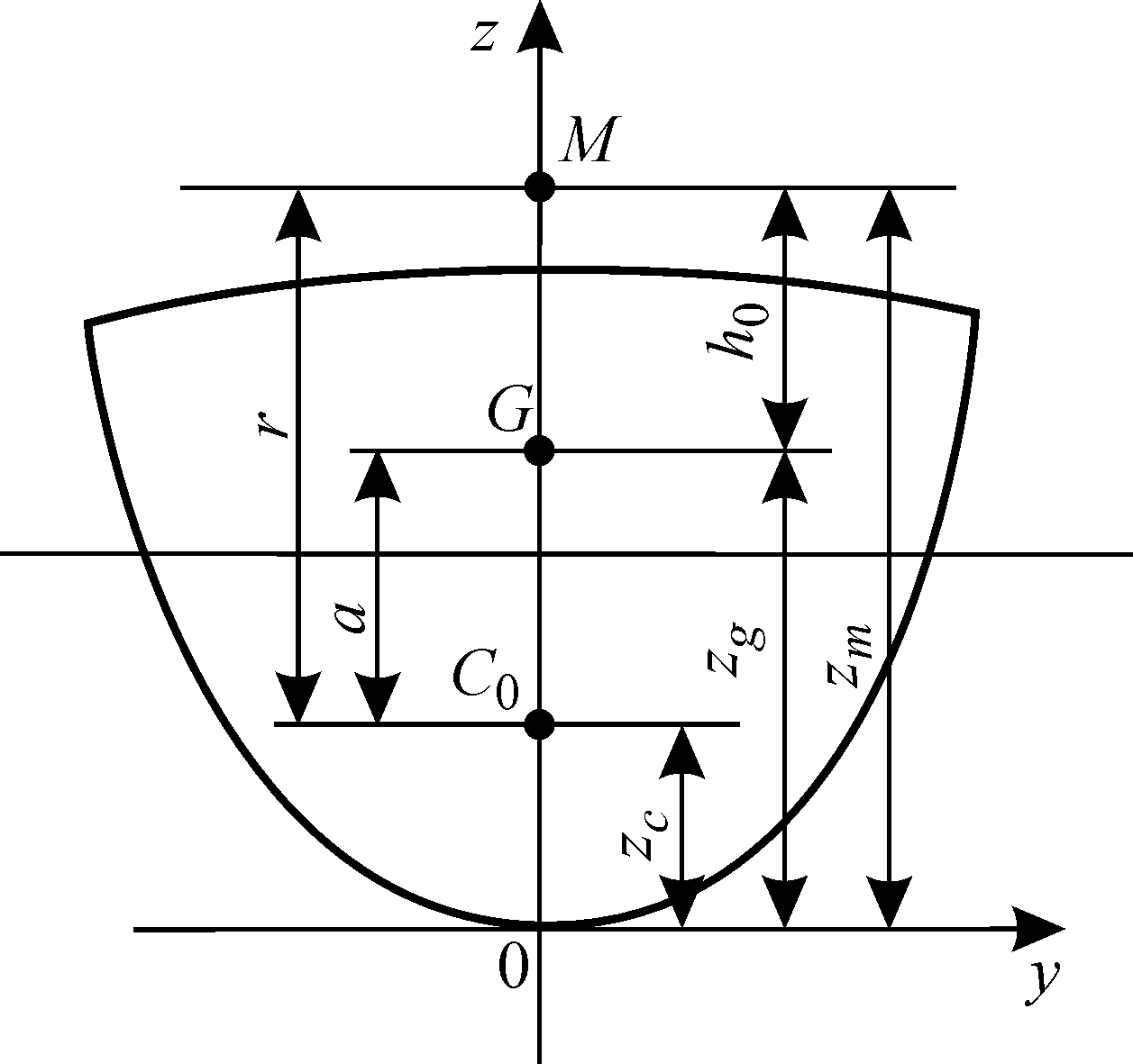
Рис.8 Определение поперечной метацентрической высоты
Аналогичным образом из рис.9 следует,
![]() ;
(19)
;
(19)
![]() ;
(20)
;
(20)
![]() ;
(21)
;
(21)
![]() .
(22)
.
(22)
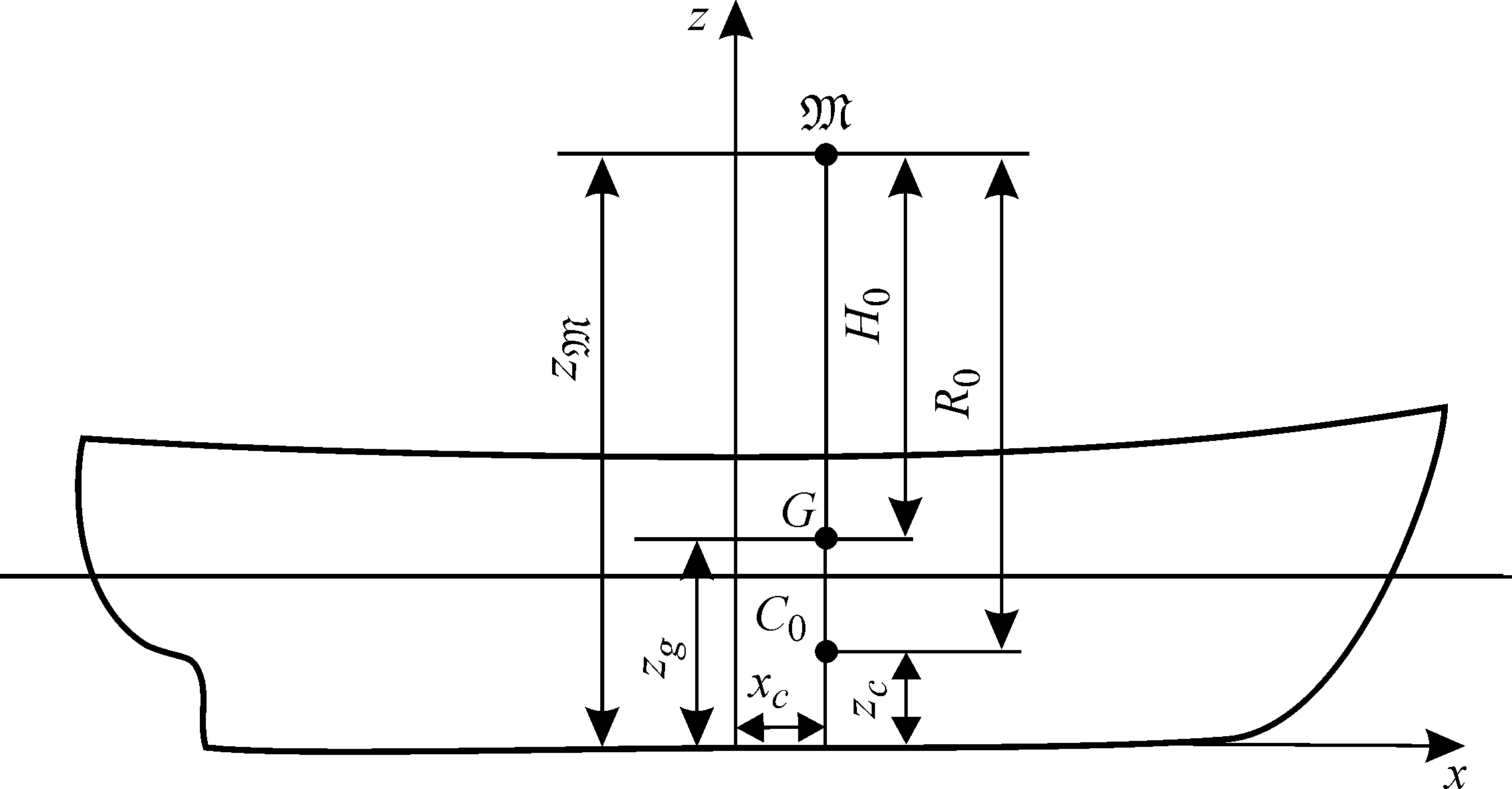
Рис.9 Определение продольной метацентрической высоты
В формулах (15) – (22)
![]() -
(23)
-
(23)
превышение ЦТ над ЦВ.
Формулы (16) и (20) являются основными для расчета метацентрических высот.
