
- •Индивидуальные задания Вариант 1 Случайные события
- •Случайные величины
- •Вариант 2 Случайные события
- •Случайные величины
- •Вариант 3 Случайные события
- •Случайные величины
- •Вариант 4 Случайные события
- •Случайные величины
- •Вариант 5 Случайные события
- •Случайные величины
- •Вариант 6 Случайные события
- •Случайные величины
- •Вариант 7 Случайные события
- •Случайные величины
- •Вариант 8 Случайные события
- •Случайные величины
- •Вариант 9 Случайные события
- •Случайные величины
- •Вариант 10 Случайные события
- •Случайные величины
- •Вариант 11 Случайные события
- •Случайные величины
- •Вариант 12 Случайные события
- •Случайные величины
- •Вариант 13 Случайные события
- •Случайные величины
- •Вариант 14 Случайные события
- •Случайные величины
- •Вариант 15 Случайные события
- •Случайные величины
- •Вариант 16 Случайные события
- •Случайные величины
- •Вариант 17 Случайные события
- •Случайные величины
- •Вариант 18 Случайные события
- •Случайные величины
- •Вариант 19 Случайные события
- •Случайные величины
- •Вариант 20 Случайные события
- •Случайные величины
- •Вариант 21 Случайные события
- •Случайные величины
- •Вариант 22 Случайные события
- •Случайные величины
- •Вариант 23 Случайные события
- •Случайные величины
- •Вариант 24 Случайные события
- •Случайные величины
- •Вариант 25 Случайные события
- •Случайные величины
- •Вариант 26 Случайные события
- •Случайные величины
- •Вариант 27 Случайные события
- •Случайные величины
- •Вариант 28 Случайные события
- •Случайные величины
- •Вариант 29 Случайные события
- •Случайные величины
- •Вариант 30 Случайные события
- •Случайные величины
Случайные величины
Случайная величина X задана функцией распределения

Найдите плотность распределения вероятностей и числовые характеристики этой случайной величины.
Две игральные кости бросают два раза. Напишите закон распределения дискретной случайной величины X – числа выпадений четного числа очков на двух игральных костях. Найдите математическое ожидание и функцию распределения F(x). Постройте многоугольник распределения и график F(x).
Найдите числовые характеристики равномерно распределенной в интервале
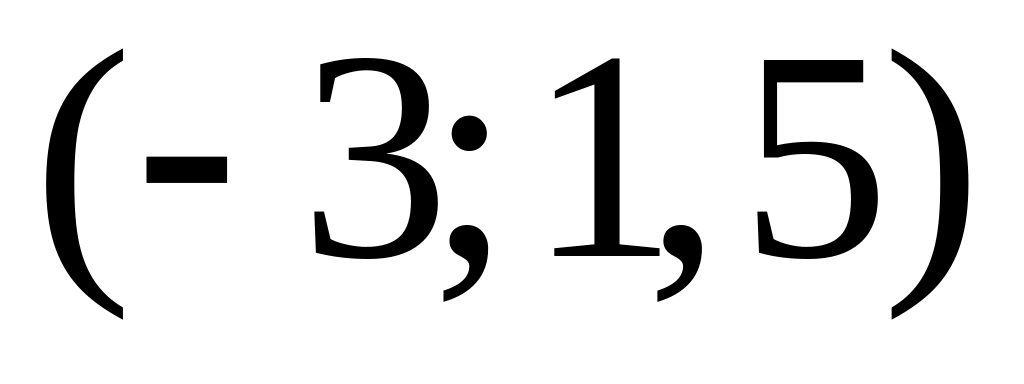 случайной величины. Запишите
дифференциальную и интегральную функции
распределения, постройте их графики.
Вычислите вероятность попадания этой
случайной величины в интервал
случайной величины. Запишите
дифференциальную и интегральную функции
распределения, постройте их графики.
Вычислите вероятность попадания этой
случайной величины в интервал
 и покажите эту вероятность на графике.
и покажите эту вероятность на графике.Размер деталей задан полем допуска 50 – 60 мм. На заводе средний размер таких деталей 5,6 см, а среднее отклонение – 0,6 см. Какова вероятность получения бракованной детали с этого завода, если ее размер подчиняется нормальному закону распределения?
