I.9. Энергия электростатического поля
Электростатические
силы взаимодействия консервативны,
следовательно, система зарядов
обладает потенциальной энергией. Пусть
имеется уединенный проводник, заряд
емкость и потенциал которого соответственно
равны
,
и
.
Увеличим заряд этого проводника на
.
Это связано с совершением работы
по преодолению кулоновских сил
отталкивания между одноименными
зарядами. Совершаемая работа идет на
увеличение электрической энергии
заряженного проводника. Следовательно,
элементарная работа
,
совершаемая внешними силами при переносе
малого заряда
из бесконечности на уединенный проводник,
равна
где
потенциал проводника, начало отсчета
которого выбрано в бесконечно удаленной
точке.
Работа, совершаемая
при увеличении потенциала проводника
от 0 до
,
то есть при сообщении проводнику заряда
,
равна
(1.45)
Энергия заряженного уединенного проводника равна той работе, которую необходимо совершить, чтобы зарядить этот проводник, то есть
(1.46)
Определим энергию
заряженного конденсатора. Если
заряд
конденсатора, а
разность потенциалов между его обкладками,
то для переноса малого заряда
с одной обкладки на другую внешние
силы
должны совершить работу
Следовательно, работа по увеличению заряда конденсатора от 0 до равна
Соответственно, энергия заряженного конденсатора
(1.47)
Учитывая, что
конденсатор – это система из двух
проводников 1 и 2,
заряды которых
и
,
формулу (1.47) можно переписать
в
следующем виде:
Отсюда вытекает, что энергия системы из n неподвижных заряженных проводников
(1.48)
где
заряд
i-проводника;
потенциал, создаваемый в той точке, где
находится заряд
,
всеми зарядами, кроме i-го.
Используя выражение
(1.47), можно определить механическую
силу,
с которой пластины конденсатора
притягивают друг друга. Для этого
предположим, что расстояние х между
обкладками меняется на величину dx.
Тогда действующая сила совершает
работу
за счет уменьшения потенциальной энергии
системы
откуда
где
Тогда искомая механическая (пондеромоторная) сила равна
где знак «минус» указывает, что сила F является силой притяжения.
Преобразуем выражение
(1.47), подставив в него
и
.
Тогда получим формулу, связывающую
энергию электростатического поля
плоского конденсатора с напряженностью
(1.49)
где
объем
конденсатора.
Объемная плотность энергии (энергия единицы объема) электростатического поля определяется как
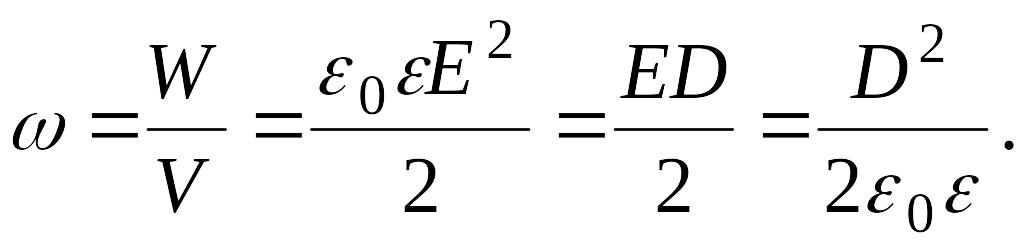(1.50)
Краткие выводы
Электрическое поле – это особая форма существования материи, связанная с электрическими зарядами и осуществляющая взаимодействие между заряженными телами. Электрический заряд является физической величиной, определяющей интенсивность электромагнитных взаимодействий.
Суммарный заряд электрически изолированной системы не изменяется (закон сохранения электрического заряда). Электрические заряды не создаются и не исчезают, они лишь передаются от одного тела к другому или перераспределяются внутри данного тела.
Раздел электродинамики, в котором изучается взаимодействие неподвижных электрических зарядов, называется электростатикой. Такое взаимо-действие осуществляется посредством электростатического поля.
Неподвижные точечные электрические заряды взаимодействуют в вакууме с силой, определяемой законом Кулона:
Силовой характеристикой электростатического поля является напряженность. Она численно равна силе, действующей со стороны поля на единичный положительный заряд, помещенный в данную точку поля:
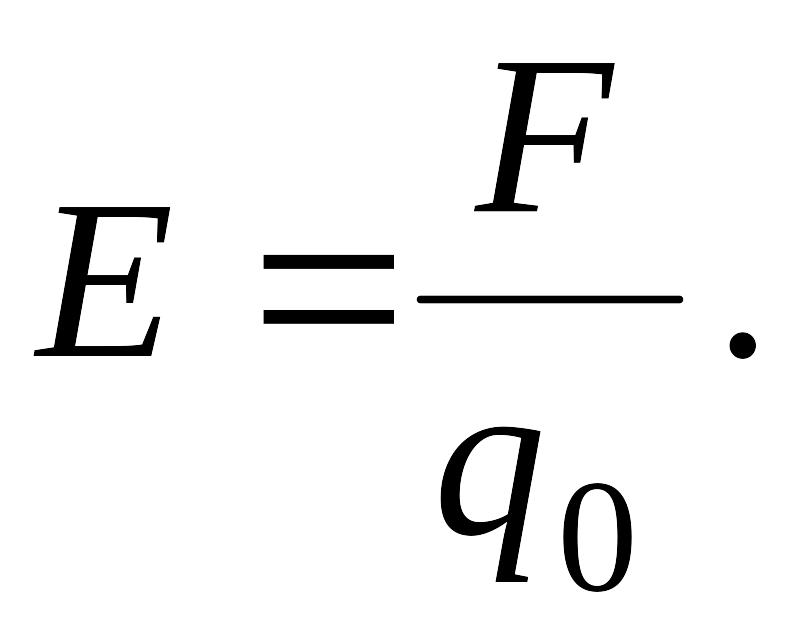
Напряженности полей, создаваемых отдельными зарядами, складываются геометрически (принцип суперпозиции):
Электростатическое поле является потенциальным, то есть работа, совершаемая при перемещении заряда, не зависит от траектории, а определяется лишь начальным и конечным положениями заряда. Эта работа численно равна изменению потенциальной энергии:
Энергетической характеристикой поля является потенциал. Он характеризует потенциальную энергию, которой обладал бы положительный единичный заряд, помещенный в данную точку поля:
Потенциал в какой-либо точке электрического поля, образованного системой зарядов, равен алгебраической сумме потенциалов, создаваемых каждым зарядом системы:
Разность потенциалов – это скалярная физическая величина, опре-деляемая работой, совершаемой кулоновскими силами при перемещении положительного единичного заряда из одной точки поля в другую:
Силовая и энергетическая характеристики поля связаны между собой соотношением
то есть напряженность поля равна градиенту потенциала со знаком «минус». Это означает, что вектор напряженности электростатического поля направлен в сторону убывания потенциала. В случае однородного поля (например, поля плоского конденсатора) модуль напряженности определяется по формуле
Вычисление напряженности поля большой системы электрических зарядов с помощью принципа суперпозиции электростатических полей можно упростить, используя теорему Гаусса:
то есть поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на электрическую постоянную.
При внесении диэлектрика во внешнее электрическое поле происходит его поляризация. Поляризованный диэлектрик создает собственное поле, которое внутри диэлектрика ослабляет внешнее электрическое поле в раз:
Теорема Гаусса для электростатического поля в диэлектрике формулируется следующим образом: поток вектора смещения электростатического поля в диэлектрике сквозь произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности свободных электрических зарядов, то есть
Способность проводника накапливать электрические заряды характеризуется электрической емкостью:
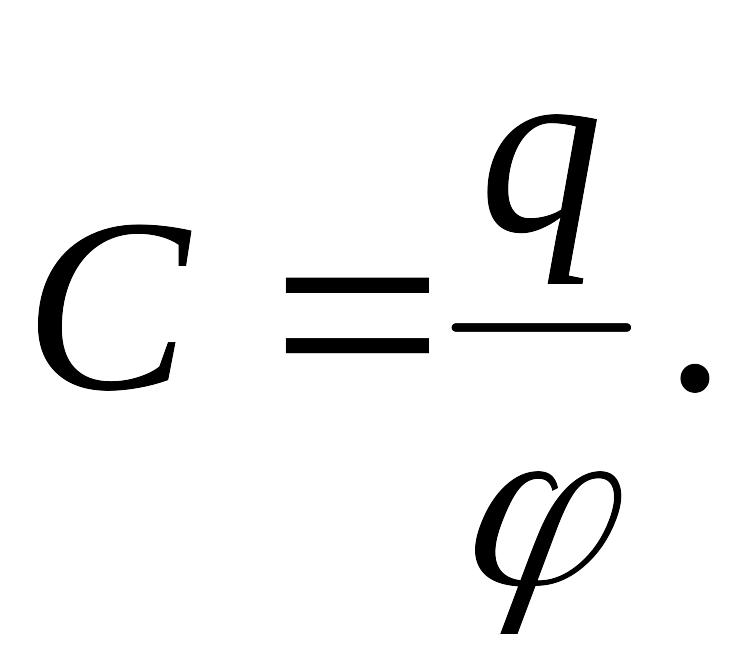
Электрическая емкость не зависит от заряда проводника, а определяется его геометрическими размерами и формой, расположением относительно других проводников и электрическими свойствами окружающей среды.
Емкостью конденсатора называется физическая величина, равная отношению заряда , накопленного в конденсаторе, к разности потенциалов между его обкладками:
Электрическая емкость плоского конденсатора
Заряженный конденсатор обладает энергией
Энергия конденсатора сосредоточена в электрическом поле. Объемная плотность энергии электростатического поля определяется следующим образом: