VII.4. Поляризация света

Как отмечалось выше, свет представляет собой электромагнитные колебания, распространяющиеся в виде электромагнитных волн с длиной волны порядка (3,8-7,6)∙10^-7 м. Электромагнитная волна характеризуется вектором напряженности электрического поля и вектором напряжен-ности магнитного поля. Эти векторы расположены во взаимно перпендикулярных плоскостях и колеблются в одинаковых фазах (рис. 6.21).

Колебания векторов и в изотропной среде (среде, физические свойства которой одинаковы во всех направлениях) происходят перпендикулярно направлению распространения колебаний. Поэтому электромагнитные волны относятся к типу поперечных волн.

В большинстве случаев воздействие световых волн определяется вектором напряженности электрического поля, так как явления, наблюдаемые в веществе под действием света (люминесценция, фотоэффект и др.), связаны с воздействием на электроны.

Чтобы выяснить, какое из полей оказывает большее воздействие на электроны вещества, рассмотрим отношение сил, действующих на электрон со стороны электрического и магнитного полей:

 

где v – скорость движения электрона.

Отношение напряженностей магнитного и электрического полей

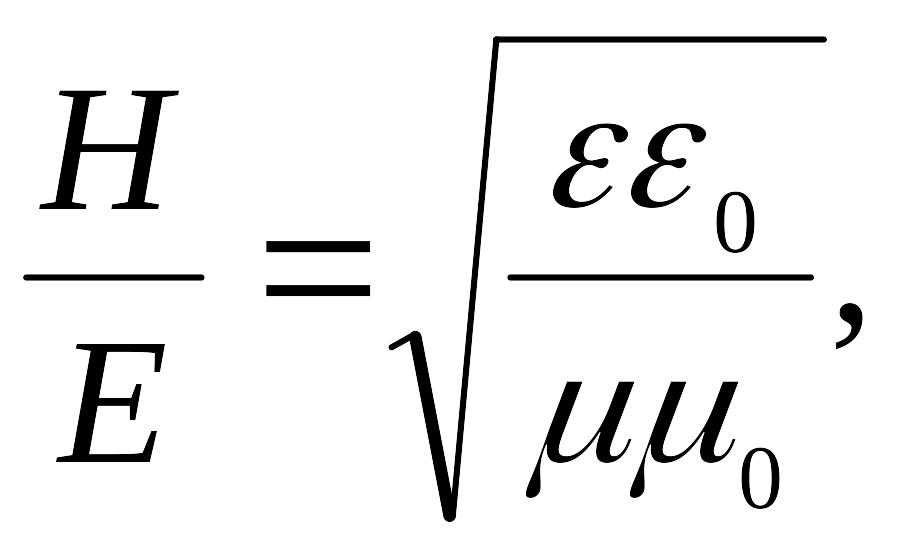
тогда



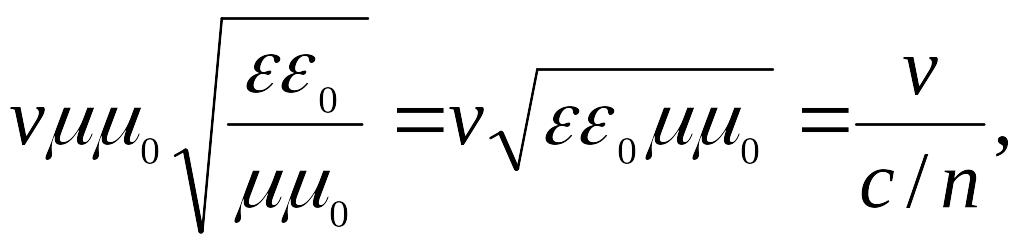
где – величина, обратная скорости света в среде. Так как , то . Поэтому, говоря о колебаниях в световом луче, понимают колебания вектора , который называют световым вектором.

Электромагнитные волны, излучаемые светящимся телом, – это результат отдельных волн, которые испускаются его атомными осцилляторами. Вследствие того, что атомы беспрерывно изменяют свою пространственную ориентацию, изменяется с большой частотой и направление колебаний вектора результирующей световой волны.

Если в световой волне колебания вектора напряженности электри-ческого поля происходят по всевозможным направлениям в плоскости, перпендикулярной направлению распространения (к лучу), то свет называют естественным (рис. 7.15, а; луч перпендикулярен плоскости рисунка). Равномерное распределение векторов объясняется большим числом атомных излучателей, а равенство амплитудных значений – в среднем одинаковой интенсивностью излучения каждого из атомов.

Свет, в котором колебания светового вектора каким-то образом упорядочены, называют поляризованным.

Ч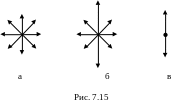 астично поляризованным называется свет с преимущественным направлением колебаний вектора (рис. 7.15, б). Если колебания вектора (а, следовательно, и ) происходят только в одном направлении, перпендикулярном лучу, то свет называют плоскополяризованным (рис. 7.15, в).

П лоскость, проходящая через направление колебаний светового вектора плоскополяризованной волны и через луч (направление распространения этой волны), называется плоскостью поляризации (рис. 7.16, плоскость А). Плоскость, проходящая через луч и перпендикулярная направлению колебаний вектора (плоскость D), в которой колеблется вектор , называется плоскостью колебаний.

Прибор, превращающий естественный свет в поляризованный, называют поляризатором. Он пропускает колебания, например, параллельные главной плоскости поляризатора и полностью задерживает колебания, перпендикулярные этой плоскости. В качестве поляризаторов могут использоваться среды, анизотропные в отношении колебаний вектора .

Прибор, определяющий направление колебаний (гасящий поляризованную волну) и предназначенный для анализа степени поляризации света, называют анализатором.

Степенью поляризации света называют величину

где I_max, I_min – соответственно максимальная и минимальная интенсивность частично поляризованного света, пропускаемого анализатором. Для естественного света I_max = I_min и Р=0, для плоскополяризованного света I_max = 0 и Р=1.

Один из способов получения поляризованного света состоит в использовании явления отражения и преломления света на поверхности диэлектрика. Пусть на черное зеркало (в этом зеркале устранено отражение от второй поверхности) падает естественный свет. Световые колебания, как и любые колебания, происходящие в одной плоскости, можно разложить по правилу параллелограмма на два колебания, происходящие в двух взаимно перпендикулярных плоскостях. Следовательно, естественный луч света можно представить как луч, в котором колебания происходят в двух взаимно перпендикулярных направлениях, например, в плоскости чертежа, которую считаем совпадающей с плоскостью падения (условно отмечаются стрелками) и в плоскости перпендикулярной (отмечаются точками). Эти два вида колебаний по-разному отражаются от зеркала из диэлектрика.

Если угол падения света на границу раздела двух диэлектриков (например, воздуха и стекла) с показателями преломления n₁ и n₂ не равен нулю, то отраженный и преломленный лучи оказываются частично поляризованными (рис. 7.17). В отраженном свете преобладают колебания, перпендикулярные плоскости падения, в преломленном луче – колебания, параллельные плоскости падения.

С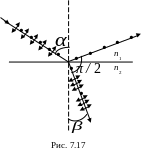 тепень поляризации зависит от угла падения . При угле падения, удовлетворяющем условию

(7.16)

(n₂₁ – показатель преломления второй среды относительно первой), отраженный луч полностью поляризован, а преломленный луч поляризован максимально, но не полностью. Соотношение (7.16) называется законом Брюстера. Угол называют углом Брюстера или углом полной поляризации.

Из закона Брюстера и закона преломления следует, что при падении света на диэлектрик под углом луч, отраженный под этим углом, и луч преломленный взаимно перпендикулярны.

Двойное лучепреломление. В природе существуют кристаллы (например, исландский шпат), которые дают двойное лучепреломление. Это явление объясняется следующим образом.

Кристаллы – тела анизотропные, то есть их физические свойства, например, скорость распространения световых колебаний, различны в разных направлениях. Но особенностью кристалла является то, что в нем можно выделить оптическую ось. Она характеризуется тем, что свойства кристалла одинаковы во всех направлениях, которые составляют с оптической осью кристалла любые равные углы. Необходимо отметить, что оптическая ось не есть определенная линия, а только определенное направление. Плоскость, проходящая через падающий луч и оптическую ось кристалла, называется главным сечением кристалла.

Скорость распространения света в кристалле зависит от угла между направлением колебаний и направлением главной оси кристалла: .

Если луч света идет вдоль оптической оси кристалла, то все его колебания перпендикулярны оптической оси ( =90⁰) и, следовательно, распространяются с одной и той же скоростью. Луч в этом случае не раздваивается, и двойного изображения нет.

Если луч света падает под некоторым углом к оптической оси кристалла, то можно разложить колебания в падающем луче на два взаимно перпендикулярных колебания: колебания, происходящие в плоскости сечения, и колебания, происходящие в плоскости, перпендикулярной главному сечению.

Колебания, перпендикулярные главному сечению кристалла (обозначены точками), распространяются в кристалле с той же скоростью, что и колебания луча, идущего вдоль оптической оси, так как при любом угле падения они составляют с осью кристалла угол 90⁰.

Колебания, происходящие в плоскости главного сечения кристалла (обозначены стрелками), распространяются с другой скоростью, так как они составляют с осью кристалла другой угол, равный 90⁰- .

Так как скорость распространения колебаний в кристалле зависит от угла , то есть , то колебания, перпендикулярные главному сечению, и колебания, лежащие в плоскости главного сечения, распространяются в кристалле с различной скоростью и, следовательно, имеют различный показатель преломления. Но при различном показателе преломления различны и углы преломления. В этом случае луч света раздваивается и дает двойное изображение. Лучи, колебания в которых перпендикулярны плоскости главного сечения, называют обыкновенными; лучи, колебания в которых происходят в плоскости главного сечения, называют необыкновенными.

Лучи обыкновенные и необыкновенные являются поляризованными лучами: обыкновенный луч поляризован в плоскости главного сечения, а необыкновенный луч – в плоскости, перпендикулярной плоскости главного сечения.

Призма Николя. Закон Малюса. Устройства, служащие для получения поляризованного света, называют поляризационными призмами. Поляризационная призма может служить и анализатором. Поляризационную призму Николя часто называют просто николь. Она представляет собой кристалл исландского шпата, имеющий форму параллелепипеда (рис. 7.18).

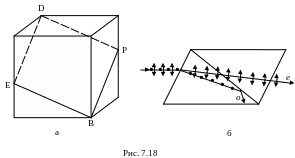
Кристалл разрезается наклонно по плоскости BEDP на две части, а затем склеивается канадским бальзамом. Показатель преломления канадского бальзама n=1,549. Показатель преломления исландского шпата для обыкновенных лучей n_о=1,658. Для необыкновенных лучей показатель преломления исландского шпата различен для разных направлений: для лучей, идущих параллельно длинным ребрам призмы, он равен n_e=1,515.

Пусть естественный луч падает на нижнюю грань призмы (рис. 7.18, б) в плоскости главного сечения (плоскости чертежа) под таким углом, что преломленные лучи, раздвоившись, идут почти параллельно продольным ребрам. Необыкновенный луч (е), дойдя до слоя канадского бальзама, вступает в него как в тело, более преломляющее и продолжает путь, не отклоняясь, так как слой канадского бальзама очень тонок. Обыкновенный же луч (о) встречает слой бальзама как среду менее преломляющую, и так как угол падения его больше предельного угла, то этот луч испытывает полное отражение и поглощается зачерненной гранью призмы. Из призмы выходит один только необыкновенный луч, колебания в котором параллельны главному сечению.

Если на анализатор падает поляризованный луч, плоскость поляризации которого составляет угол с плоскостью поляризации анализатора, то интенсивность прошедшего через анализатор луча определяется законом Малюса:

, (7.17)

где – интенсивность луча, падающего на анализатор; I – интенсивность луча, выходящего из анализатора, без учета потерь в анализаторе в результате поглощения и рассеяния света.

Если пропустить естественный свет через два поляризатора, плоскости которых образуют угол , то из первого выйдет плоскополяризованный свет интенсивностью , а из второго – свет интенсивностью . Таким образом, интенсивность света, прошедшего через два поляризатора,

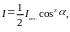
откуда (поляризаторы параллельны) и (поляризаторы скрещены). В последнем случае будет полное затмение поля зрения.