VI.5. Уравнения электромагнитной волны
Основу теории электромагнитного поля составляют уравнения Максвелла (эти уравнения в электродинамике играют такую же роль, что и законы Ньютона в классической механике). Уравнения Максвелла отражают тот факт, что источниками электрического поля могут быть либо электрические заряды, либо изменяющиеся во времени магнитные поля. Магнитные поля могут возбуждаться либо движущимися электрическими зарядами (токами), либо переменными электрическими полями.
Таблица 6.1
Вид излучения |
, м |
, Гц |
Источник излучения |
Радиоволны |
103 – 10-4 |
3·105 - 3·1012 |
Колебательный контур, вибратор Герца, высокочастотный генератор |
Световые волны: – инфракрасное излучение – видимый свет – ультрафиолетовое излучение |
5·10-4 - 8·10-7 8·10-7 - 4·10-7
4·10-7 - 10-9
|
6·1011 - 4·1014 4·1014 – 7,5·1014
7,5·1014 – 3·1017
|
Лампы, лазеры |
Рентгеновское излучение
|
2·10-9 - 6·10-12
|
1,5·1017 – 5·1019
|
Рентгеновские трубки |
-излучение |
< 6·10-12 |
> 5·1019 |
Ядерные реакции, космические процессы |
Уравнения Максвелла приводились в главе 5 учебного пособия. Для удобства дальнейшего изложения запишем эти уравнения еще раз.
Полная система уравнений Максвелла в интегральной форме
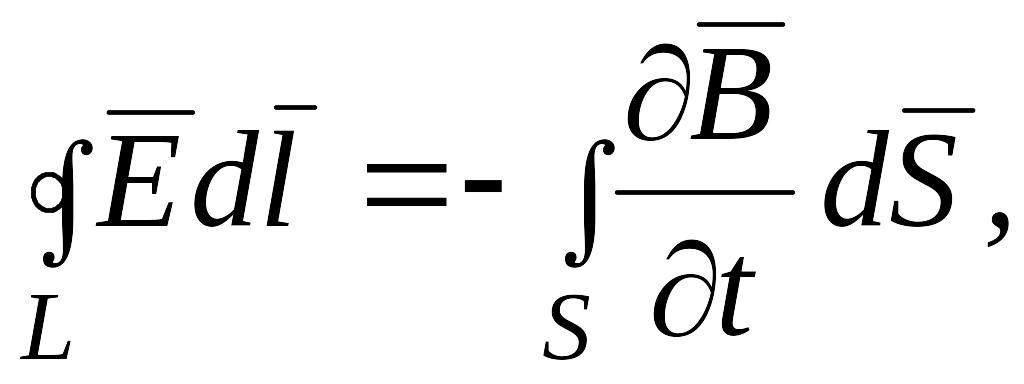(6.25)
(6.26)
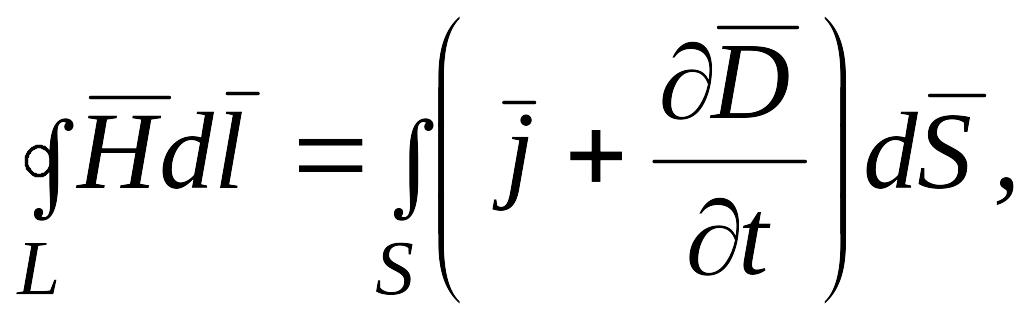(6.27)
(6.28)
Эти уравнения связывают значения или вдоль некоторого контура со значениями (соответственно ) в точках опирающейся на контур поверхности. С помощью теорем векторного анализа (теоремы Стокса и теоремы Остроградского-Гаусса) от уравнений (6.25) – (6.28) можно перейти к уравнениям в дифференциальной форме, которые связывают значения или в некоторой точке пространства с (соответственно ) в той же самой точке.
Полная система уравнений Максвелла в дифференциальной форме
(6.29)
(6.30)
(6.31)
(6.32)
Между величинами,
входящими в уравнения Максвелла,
существует следующая связь:
(6.33)
(6.34)
(6.35)
Совокупность уравнений (6.29) – (6.35) образует основу электродинамики покоящихся сред.
Под ротором вектора
(
)
подразумевается вектор с составляющими:
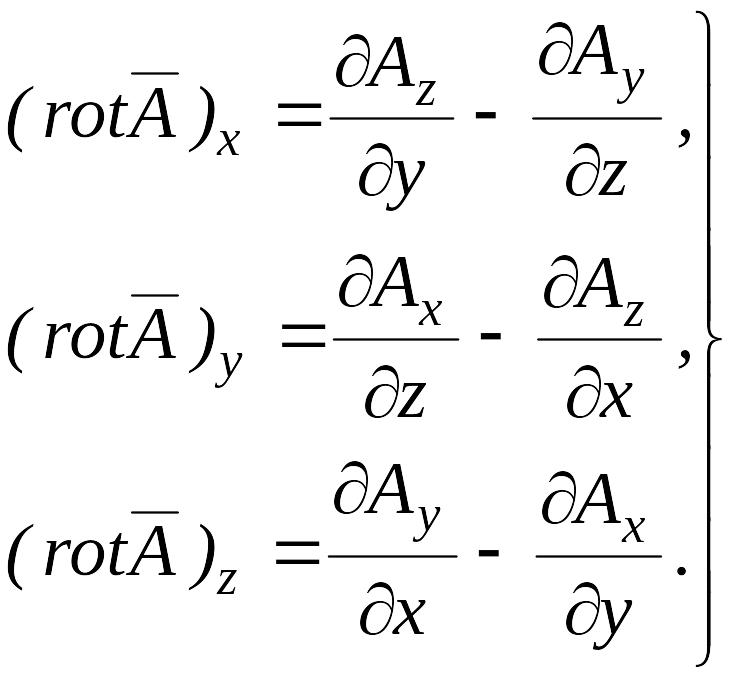(6.36)
Под дивергенцией
вектора
(
)
подразумевается следующая скалярная
величина:
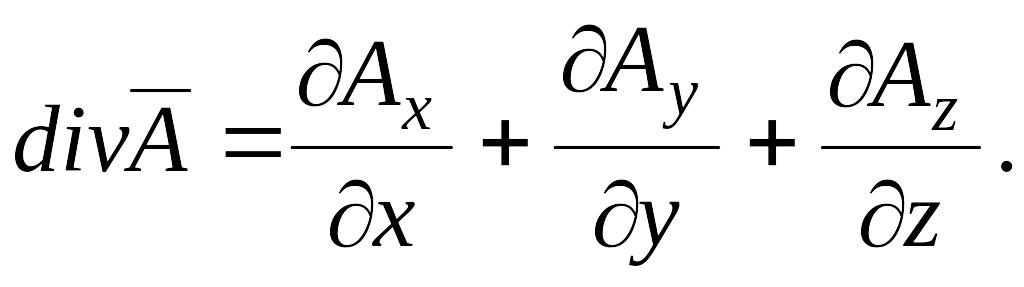(6.37)
Запишем уравнения
Максвелла для однородной нейтральной
(
)
и непроводящей (
)
среды с постоянными проницаемостями
и
.
В этом случае
Следовательно, уравнения (6.29) – (6.32) примут вид
(6.38)
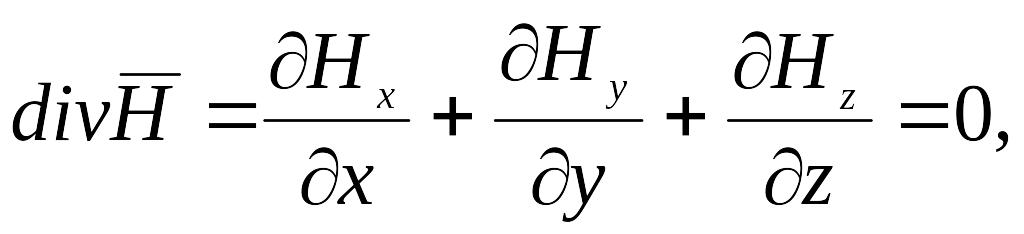(6.39)
(6.40)
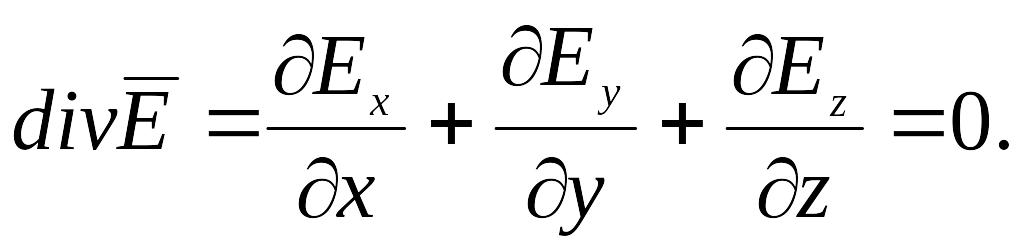(6.41)
П
рименим
к уравнению (6.38) операцию rot:
.
(6.42)
Символ rot означает дифференцирование по координатам. Меняя порядок дифференцирования по координатам и времени, можно записать
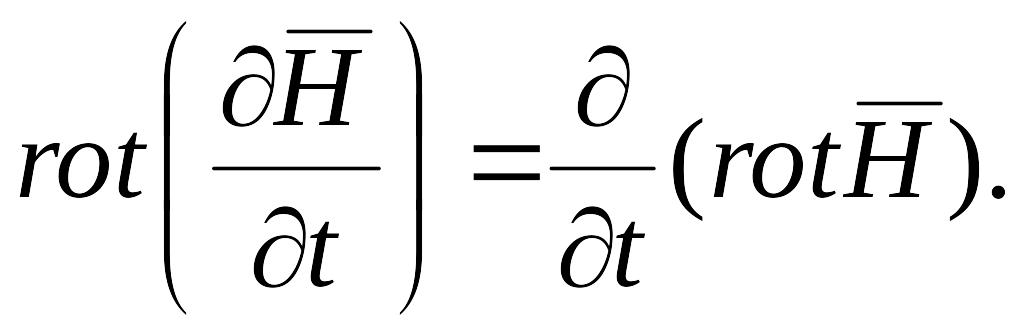
Произведя в уравнении (6.42) эту замену и подставив в получившееся выражение формулу (6.40), получим
(6.43)
Применив операцию rot к уравнению (6.40) и произведя аналогичные преобразования, получим уравнение
(6.44)
Найдем проекцию векторного уравнения (6.43) на ось х:
(6.45)
По определению ротора (см. формулы (6.36))
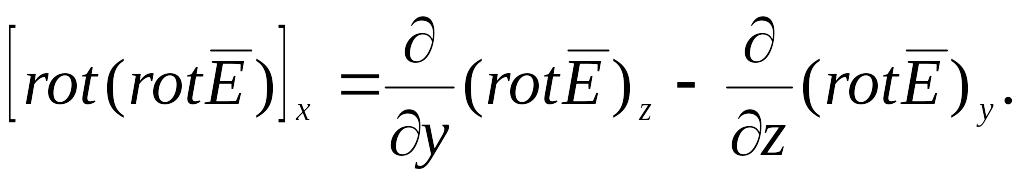
Подставляя в это
выражение значения
и
,
получим
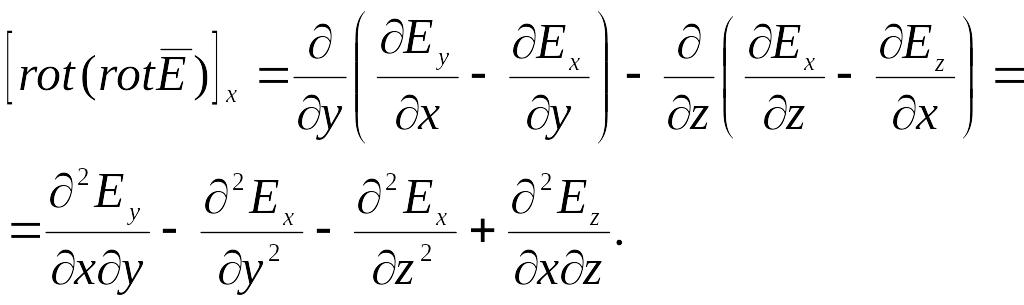
Прибавляя и вычитая
,
приведем данное выражение к виду
.
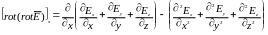
Учитывая (6.41), уравнение (6.45) можно записать следующим образом:
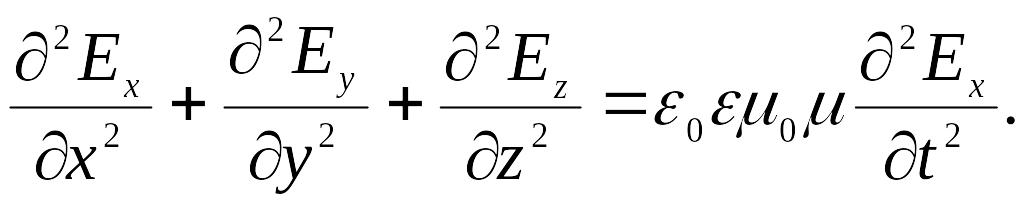(6.46)
Аналогичные уравнения
получаются для
и
.
Объединив уравнения для всех трех
компонент, получим дифференциальное
уравнение для вектора
:
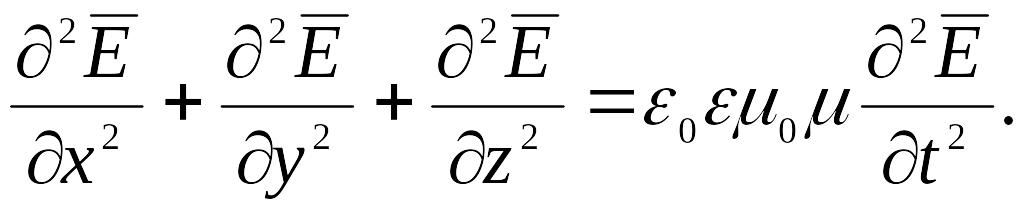(6.47)
Сходным образом уравнение (6.44) можно преобразовать к виду
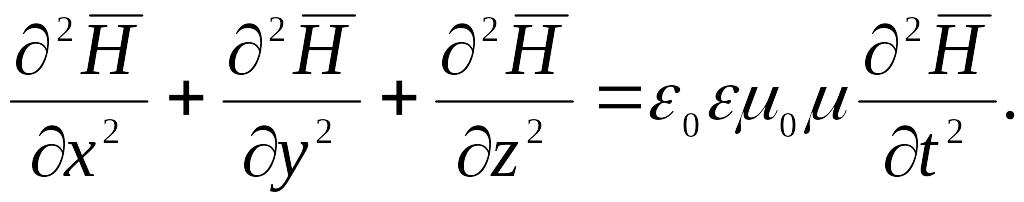(6.48)
Уравнения (6.47) и (6.48) неразрывно связаны друг с другом, так как они получены из уравнений (6.38) и (6.40), каждое из которых содержит и , и .
Как отмечалось ранее при рассмотрении механических волн, дифференциальное уравнение вида
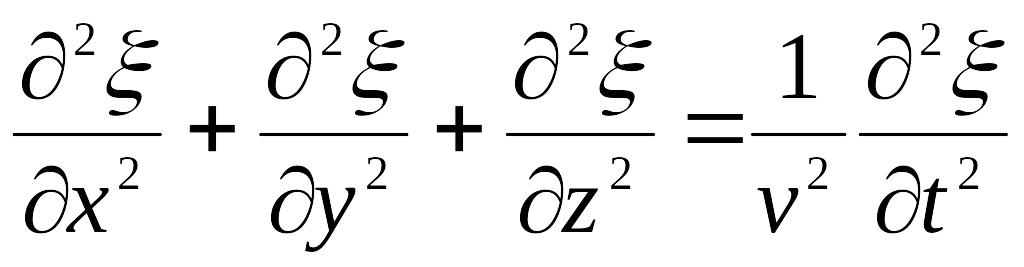
представляет собой волновое уравнение. Всякая функция, удовлетворяющая такому уравнению, описывает некоторую волну. Таким образом, уравнения (6.47) и (6.48) указывают на то, что электромагнитные поля могут существовать в виде электромагнитных волн, фазовая скорость которых равна
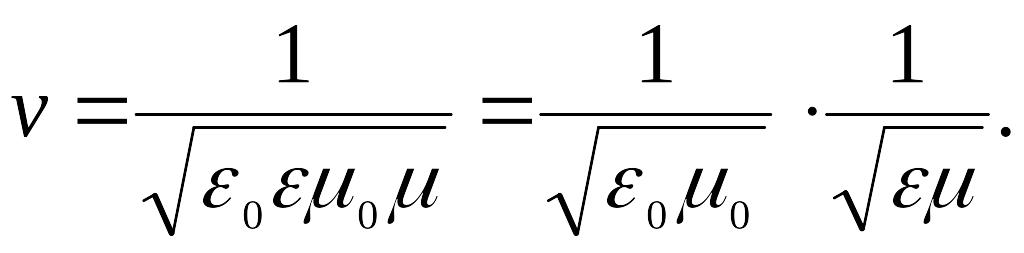(6.49)
Для вакуума по формуле (6.49) получается
Таким образом, фазовая скорость электромагнитных волн
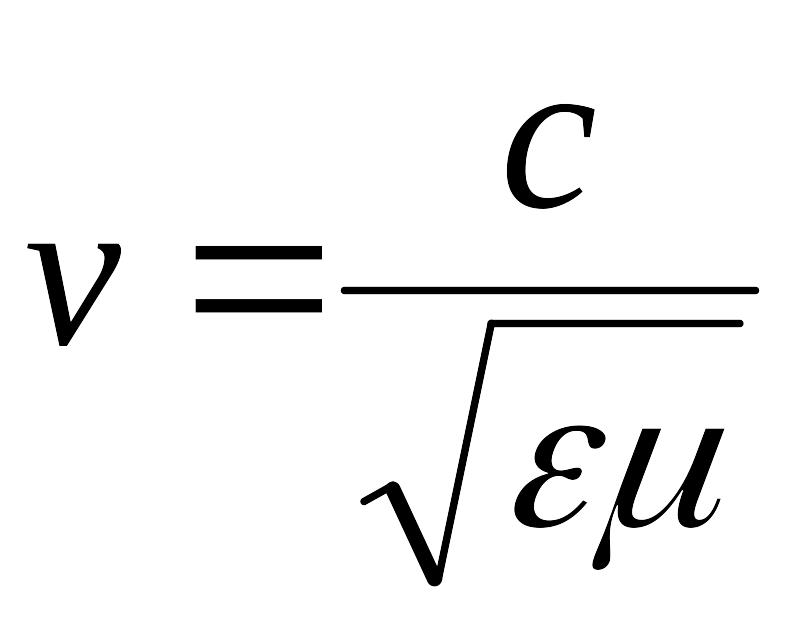(6.50)
и в вакууме совпадает со скоростью света.