
- •Предисловие
- •Введение
- •I. Электрическое поле
- •I.1. Исходные положения. Основные понятия и определения
- •I.2. Основной закон электростатики
- •I.3. Электростатическое поле. Напряженность поля
- •I.4. Циркуляция вектора напряженности электростатического поля. Потенциал поля
- •I.5. Связь между силовой и энергетической характеристиками электростатического поля
- •I.6. Теорема Гаусса для электростатического поля в вакууме
- •I.7. Диэлектрики в электростатическом поле. Теорема Гаусса для электростатического поля в диэлектрике
- •I.8. Проводники в электростатическом поле. Конденсаторы
- •I.9. Энергия электростатического поля
- •Краткие выводы
- •Вопросы для самоконтроля и повторения
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •II. Постоянный электрический ток
- •II.1. Электрический ток и его характеристики
- •II.2. Закон Ома в дифференциальной форме
- •II.3. Последовательное и параллельное соединение проводников. Электроизмерительные приборы
- •II.4. Работа и мощность тока. Закон Джоуля-Ленца
- •II.5. Закон Ома в интегральной форме
- •II.6. Расчет разветвленных цепей постоянного тока
- •Краткие выводы
- •Вопросы для самоконтроля и повторения
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •III. Магнитное поле
- •III.1. Магнитное поле и его характеристики
- •III.2. Закон Био-Савара-Лапласа
- •III.3. Магнитное поле движущегося заряда. Сила Лоренца
- •III.4. Проводник с током в магнитном поле. Закон Ампера
- •III.5. Циркуляция вектора индукции магнитного поля в вакууме
- •III.6. Теорема Гаусса для магнитного поля в вакууме
- •III.7. Магнитные свойства вещества
- •Краткие выводы
- •Вопросы для самоконтроля и повторения
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •IV. Электромагнитная индукция
- •IV.1. Закон электромагнитной индукции
- •IV.2. Явление самоиндукции. Индуктивность контура
- •IV.3. Взаимная индукция
- •IV.4. Энергия магнитного поля
- •IV.5. Практическое применение электромагнитной индукции
- •Краткие выводы
- •Вопросы для самоконтроля и повторения
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •V. Элементы теории электромагнитного поля
- •V.1. Вихревое электрическое поле
- •V.2. Ток смещения
- •V.3. Уравнения Максвелла для электромагнитного поля
- •Краткие выводы
- •Вопросы для самоконтроля и повторения
- •VI. Электромагнитные колебания и волны
- •VI.1. Свободные колебания в rlc-контуре
- •VI.2. Вынужденные колебания. Переменный электрический ток
- •VI.3. Резонанс в электрических цепях
- •VI.4. Источники электромагнитных волн
- •VI.5. Уравнения электромагнитной волны
- •VI.6. Плоская электромагнитная волна
- •VI.7. Энергия и импульс электромагнитной волны
- •Краткие выводы
- •Вопросы для самоконтроля и повторения
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •VII. Основы волновой оптики
- •VII.1. Краткая история развития представлений о природе света
- •VII.2. Интерференция света
- •VII.3. Дифракция света
- •VII.4. Поляризация света
- •VII.5. Взаимодействие электромагнитных волн с веществом
- •Краткие выводы
- •Вопросы для самоконтроля и повторения
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Заключение
- •Библиографический список
- •Основные физические величины и их единицы в си
- •Производные единицы электрических и магнитных величин
- •Элементы векторной алгебры
- •Основные законы и формулы классической электродинамики
- •Некоторые знаменательные события в истории развития электродинамики
- •Оглавление
- •Александр Фёдорович Ан
VI.2. Вынужденные колебания. Переменный электрический ток
Для
того чтобы в реальной колебательной
системе получить незатухающие
колебания, необходимо
компенсировать в ней потери энергии.
Такая компенсация возможна с помощью
какого-либо периодически действующего
внешнего фактора
![]() ,
изменяющегося, например, по гармоническому
закону
,
изменяющегося, например, по гармоническому
закону ![]() ,
,
где
![]() –
циклическая частота внешнего воздействия.
–
циклическая частота внешнего воздействия.
Если рассматривать процессы в электрическом колебательном контуре, то в качестве выступает подводимая к системе внешняя, изменяющаяся по гармоническому закону ЭДС или переменное напряжение
![]() (6.8)
(6.8)
Тогда дифференциальное уравнение вынужденных электромагнитных колебаний в колебательном контуре с учетом (6.8) будет иметь вид
![]() (6.9)
(6.9)
Решением уравнения (6.9) в установившемся режиме является гармоническая функция
![]()
где
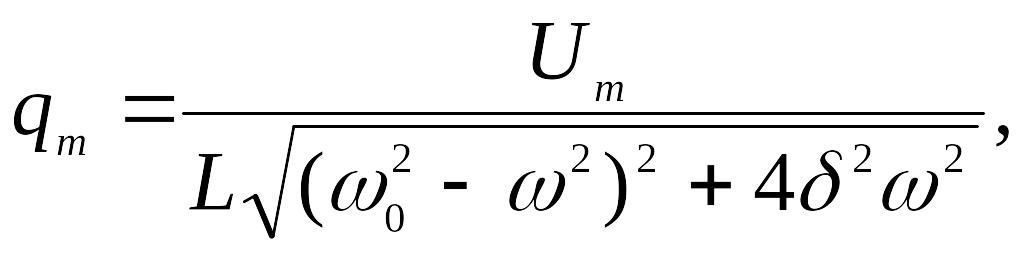
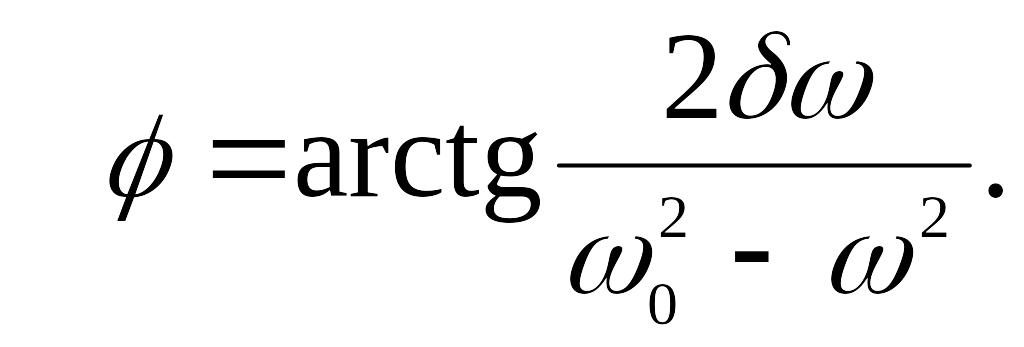
Установившиеся вынужденные электромагнитные колебания в цепи с резистором, катушкой индуктивности и конденсатором можно рассматривать как переменный электрический ток. Если подводимое к контуру внешнее напряжение периодически изменяются по гармоническому закону, то переменный ток называют синусоидальным (рис. 6.5):
![]()
или
![]()
г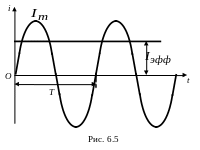 де
де
![]() – мгновенное значение силы тока, то
есть значение тока для каждого момента
времени;
– мгновенное значение силы тока, то
есть значение тока для каждого момента
времени;
![]() – амплитудное значение силы тока.
– амплитудное значение силы тока.
При частоте
![]() (промышленная частота) период
электромагнитных колебаний
составляет
(промышленная частота) период
электромагнитных колебаний
составляет
![]() .
.
Ввиду того, что в течение периода сила переменного тока изменяется, о величине такого тока судят не по мгновенным значениям, а по действующему или эффективному значению Iэфф.. При этом действие переменного тока оценивают по тепловому эффекту, который сравнивают с тепловым эффектом постоянного тока.
Действующим (эффективным) значением переменного тока называют такую величину, которая равна силе постоянного тока, выделяющего в проводнике такое же количество теплоты, что и данный переменный ток за одно и то же время. Действующее значение переменного синусоидального тока связано с его амплитудным значением соотношением
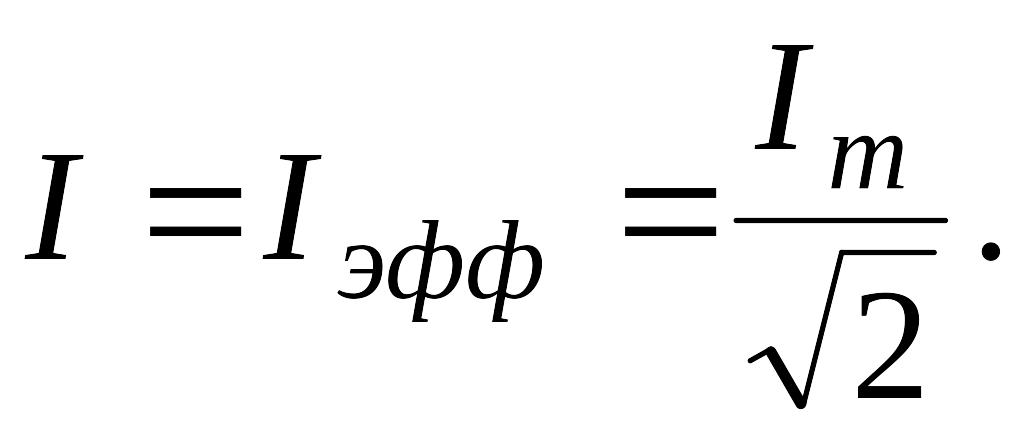
Для мгновенных значений синусоидальных токов выполняются закон Ома и правила Кирхгофа.
Рассмотрим цепи, содержащие резистор, катушку индуктивности, конденсатор и все три элемента, соединенные последовательно, на зажимах которых приложено переменное напряжение
![]()
где
![]() – амплитудное значение напряжения.
– амплитудное значение напряжения.
1. Электрическая цепь с резистором (рис. 6.6). Сила тока, протекающего через резистор, определяется законом Ома
![]()
г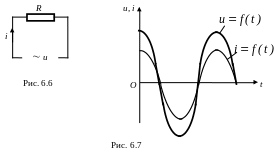 де
де
![]() – амплитуда силы тока. Очевидно, что
при чисто активном (R)
характере цепи
сдвиг фаз колебаний тока и напряжения
равен нулю (рис. 6.7).
– амплитуда силы тока. Очевидно, что
при чисто активном (R)
характере цепи
сдвиг фаз колебаний тока и напряжения
равен нулю (рис. 6.7).
2. Электрическая цепь с катушкой индуктивности (рис. 6.8). В катушке без потерь ( ) будет протекать ток, если напряжение на ее выводах компенсирует ЭДС самоиндукции, то есть
![]()
откуда ток
![]()
Постоянная интегрирования А=0, так как ток изменяется по гармони-ческому закону, то есть не имеет постоянной составляющей. Очевидно, что амплитуда тока в цепи с катушкой
![]()
где
![]() – индуктивное сопротивление,
зависящее от частоты. При
– индуктивное сопротивление,
зависящее от частоты. При
![]() (при протекании постоянного тока)
(при протекании постоянного тока)
![]() .
.
Т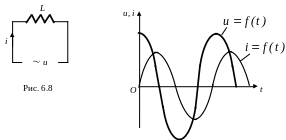 аким
образом, в цепи с катушкой индуктивности
колебания силы тока отстают по фазе на
от колебаний напряжения (рис. 6.9).
аким
образом, в цепи с катушкой индуктивности
колебания силы тока отстают по фазе на
от колебаний напряжения (рис. 6.9).
3
Рис.
6.9![]() будет равно напряжению
на зажимах
цепи, то есть
будет равно напряжению
на зажимах
цепи, то есть
![]() откуда заряд конденсатора
откуда заряд конденсатора
![]()
Сила тока в цепи конденсатора
![]()
где
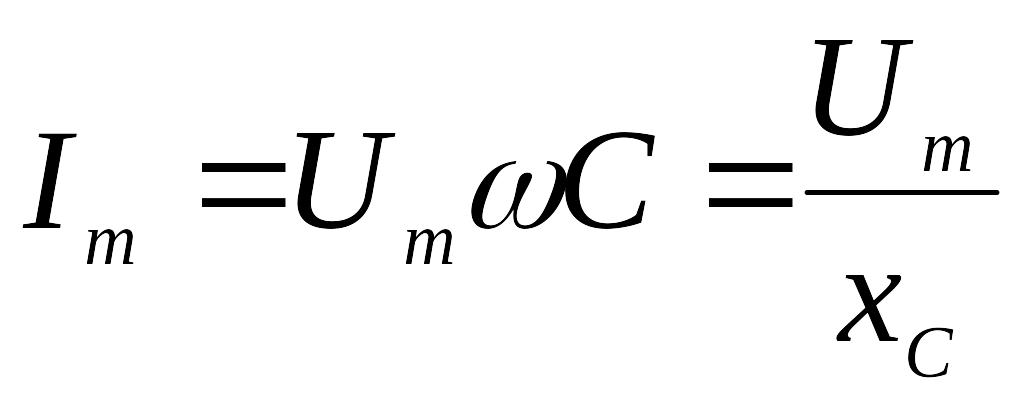 ,
,
![]() – емкостное сопротивление цепи.
Чем меньше частота
,
тем больше
– емкостное сопротивление цепи.
Чем меньше частота
,
тем больше
![]() .
Поэтому в цепи постоянного тока (
.
Поэтому в цепи постоянного тока (![]() )
)
![]() и конденсатор не проводит электрический
ток.
и конденсатор не проводит электрический
ток.
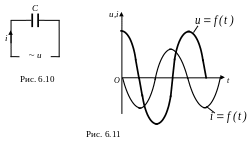
Таким образом, в цепи с конденсатором колебания силы тока опережают по фазе на колебания напряжения (рис. 6.11).
Рассмотрим теперь электрическую цепь из последовательно соединенных резистора, катушки индуктивности и конденсатора (рис. 6.12).
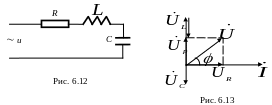
По второму правилу Кирхгофа для мгновенных значений напряжение на зажимах цепи равно сумме напряжений на отдельных элементах
![]()
Построим векторную
диаграмму цепи с учетом полученных
ранее фазовых соотношений: а) напряжение
на резисторе совпадает по фазе с током;
б) напряжение на катушке индуктивности
опережает по фазе ток на
;
в) напряжение на конденсаторе отстает
по фазе от тока на
![]() (рис. 6.13).
(рис. 6.13).
Из векторной диаграммы найдем модуль действующего значения напряжения
![]()
где
![]() –
реактивная составляющая напряжения.
–
реактивная составляющая напряжения.
Учитывая, что
![]() ,
,
![]() ,
,
![]() ,
получим
,
получим
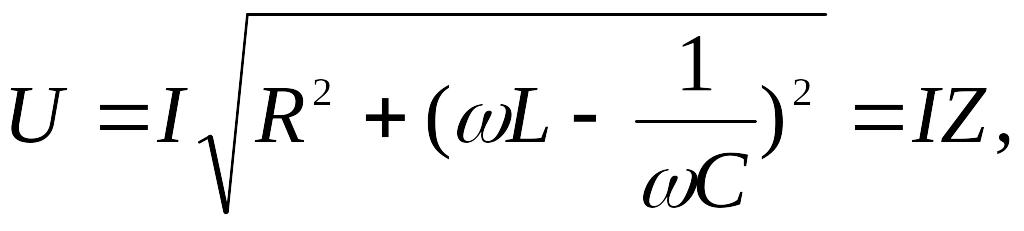
где Z – полное сопротивление цепи. Выражение
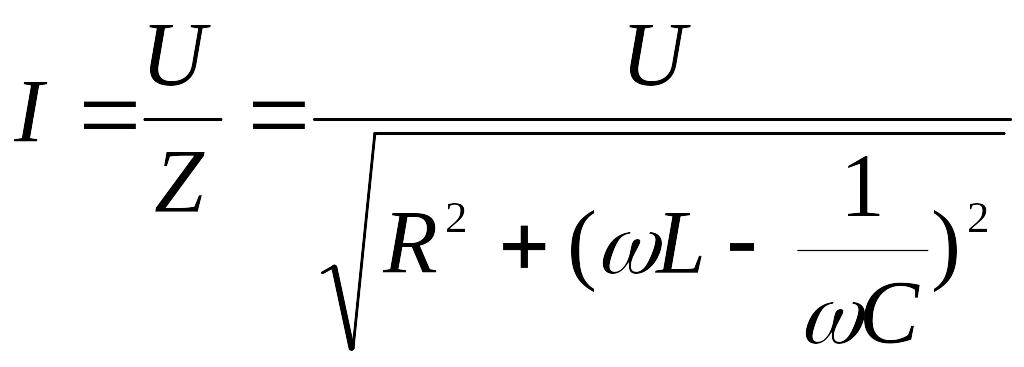 (6.10)
(6.10)
называется законом Ома для цепи переменного тока.
Разность
![]() называют реактивным сопротивлением.
Из
векторной диаграммы следует, что
угол сдвига фаз между током и напря-жением
для рассматриваемой схемы
называют реактивным сопротивлением.
Из
векторной диаграммы следует, что
угол сдвига фаз между током и напря-жением
для рассматриваемой схемы
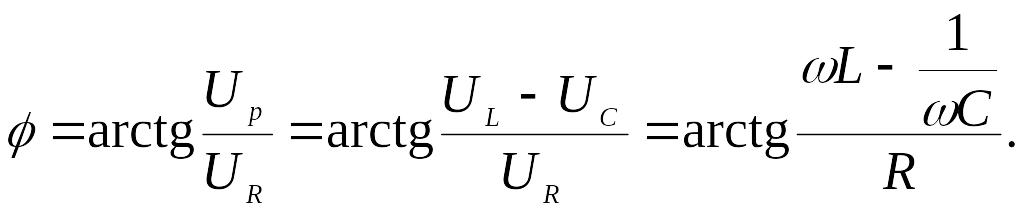 (6.11)
(6.11)
Е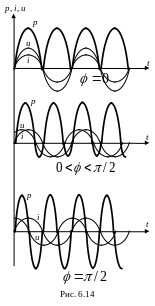 сли
сли
![]() ,
цепь имеет индуктивный характер,
,
цепь имеет индуктивный характер,
![]() ;
если
;
если
![]() ,
цепь имеет емкостный характер,
,
цепь имеет емкостный характер,
![]() ;
если
;
если
![]() ,
то реактивное сопротивление цепи
,
то реактивное сопротивление цепи
![]() ,
,
![]() и цепь имеет активный характер даже при
наличии в ней L и
C.
и цепь имеет активный характер даже при
наличии в ней L и
C.
Мгновенная мощность, развиваемая в цепи переменного тока, равна произведению мгновенных значений силы тока и напряжения:
![]()
(6.12)
Среднее за период значение мгновенной мощности называют активной мощностью тока в электрической цепи:
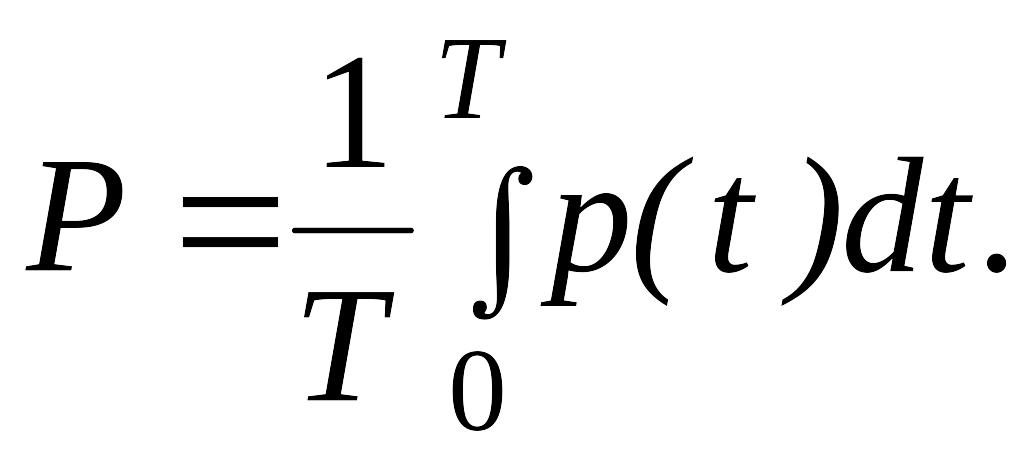 (6.13)
(6.13)
Из-за наличия сдвига
фаз
![]() знаки
у тока и напряжения в данный
момент времени могут быть разные. Поэтому
мгновенная мощность может быть
отрицательной в некоторые доли
периода переменного тока, что означает
возвращение энергии из цепи источнику
тока.
знаки
у тока и напряжения в данный
момент времени могут быть разные. Поэтому
мгновенная мощность может быть
отрицательной в некоторые доли
периода переменного тока, что означает
возвращение энергии из цепи источнику
тока.
На рис. 6.14 приведены графики изменения мгновенной мощности при различных углах сдвига фаз между колебаниями напряжения и тока.
При
в любой момент времени мощность
положительна, она
расходуется в цепи
на совершение различных видов работы.
При
![]() в отдельные промежутки времени мощность
отрицательна. Это объясняется тем, что
при наличии в цепи катушки индуктивности
возрастание тока приводит к созданию
в ней магнитного поля, которое обладает
запасом энергии. При уменьшении силы
тока магнитное поле исчезает
и
запасенная в нем энергия возвращается
к источнику тока (генератору). Аналогичный
процесс происходит при наличии в цепи
конденсатора:
в течение той четверти
периода, когда происходит зарядка
конденсатора, энергия в нем запасается,
а когда конденсатор разряжается, он
отдает в цепь запасенную энергию.
в отдельные промежутки времени мощность
отрицательна. Это объясняется тем, что
при наличии в цепи катушки индуктивности
возрастание тока приводит к созданию
в ней магнитного поля, которое обладает
запасом энергии. При уменьшении силы
тока магнитное поле исчезает
и
запасенная в нем энергия возвращается
к источнику тока (генератору). Аналогичный
процесс происходит при наличии в цепи
конденсатора:
в течение той четверти
периода, когда происходит зарядка
конденсатора, энергия в нем запасается,
а когда конденсатор разряжается, он
отдает в цепь запасенную энергию.
При
![]() положительная мощность равна отрицательной
мощности, работа тока за период равна
нулю, следовательно, средняя мощность
также равна нулю.
При этом периодически энергия запасается
в магнитном и электрическом полях,
а затем снова передается генератору.
Последний случай возможен лишь при R=0.
положительная мощность равна отрицательной
мощности, работа тока за период равна
нулю, следовательно, средняя мощность
также равна нулю.
При этом периодически энергия запасается
в магнитном и электрическом полях,
а затем снова передается генератору.
Последний случай возможен лишь при R=0.
Подставив (6.12) в (6.13) и выполнив преобразования, найдем среднее значение мощности переменного тока:
 ,
(6.14)
,
(6.14)
где
![]() – косинус угла сдвига фаз, который
называется коэффициентом мощности.
– косинус угла сдвига фаз, который
называется коэффициентом мощности.
Формула (6.14) показывает, что развиваемая в цепи переменного тока мощность зависит не только от силы тока и напряжения, но и от сдвига фаз между напряжением и током.
Коэффициент
мощности
характеризует потери энергии в цепи
и, следовательно, является важнейшей
технико-экономической характе-ристикой
при проектировании электрооборудования
переменного тока. Если нагрузки в цепи
имеют большие емкостные и индуктивные
сопротивления, то
![]() и
может быть много меньше единицы. В этих
случаях для
передачи требуемой
активной мощности Р (при заданном
напряжении)
необходимо увеличивать
силу тока, что приводит к выделению в
цепи большого количества теплоты.
Поэтому приходится либо увеличивать
сечение проводов (R1/S),
либо распределять реактивные нагрузки
так,
чтобы
был по возможности ближе к единице.
и
может быть много меньше единицы. В этих
случаях для
передачи требуемой
активной мощности Р (при заданном
напряжении)
необходимо увеличивать
силу тока, что приводит к выделению в
цепи большого количества теплоты.
Поэтому приходится либо увеличивать
сечение проводов (R1/S),
либо распределять реактивные нагрузки
так,
чтобы
был по возможности ближе к единице.
