II.2. Закон Ома в дифференциальной форме

Если в цепи на носители тока действуют только силы электростати-ческого поля, то происходит перемещение зарядов от точек с большим потенциалом к точкам с меньшим потенциалом. Это приводит к выравниванию потенциалов во всех точках цепи и к исчезновению тока. Поэтому для поддержания постоянного электрического тока в цепи необходимо наличие устройства, способного создавать и поддерживать разность потенциалов за счет работы некоторых сторонних сил. Такие устройства называют источниками тока.

Под действием сторонних сил носители тока движутся внутри источника электрической энергии против сил электростатического поля (против кулоновских сил, вызывающих соединение разноименных зарядов, а, следовательно, выравнивание потенциалов и исчезновение тока), так что на концах внешней цепи поддерживается постоянная разность потенциалов и в цепи протекает постоянный электрический ток.

Сторонние силы совершают работу по перемещению электрических зарядов. Физическая величина, определяемая работой сторонних сил при перемещении единичного положительного заряда, называется электродвижущей силой (ЭДС) источника:

(2.3)

Единица ЭДС – вольт (В).

Сторонняя сила, действующая на заряд , может быть выражена через напряженность поля сторонних сил

Тогда работа сторонних сил по перемещению заряда на замкнутом участке цепи будет равна

(2.4)

Разделив (2.4) на и учитывая (2.3), получим выражение для ЭДС, действующей в цепи,

то есть ЭДС, действующая в замкнутой цепи, есть циркуляция вектора напряженности поля сторонних сил. Как частный случай, ЭДС на участке 1-2 цепи равна

(2.5)

На заряд помимо сторонних сил действуют также силы электростатического поля (кулоновские силы) Таким образом, результирующая сила, действующая в цепи на заряд , определяется следующим образом:

Тогда работа, совершаемая этой силой над зарядом на участке 1-2 цепи, равна

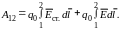
Используя выражение (2.5) и ранее полученное соотношение 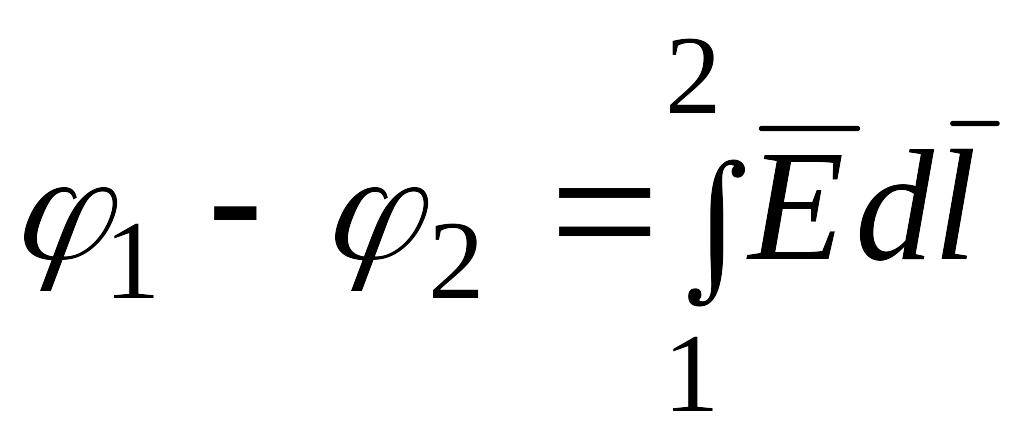, можем записать

(2.6)

Для замкнутой цепи работа электростатических сил равна нулю, поэтому в такой цепи

Разделив (2.6) на , получим

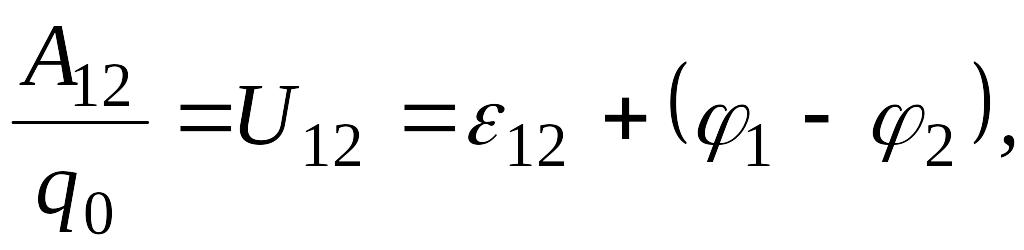(2.7)

то есть напряжением на участке цепи называется физическая величина, определяемая работой, совершаемой суммарным полем кулоновских и сторонних сил при перемещении единичного положительного заряда.

Таким образом, напряжение является более широким понятием, чем разность потенциалов: напряжение на участке цепи равно разности потенциалов только в том случае, если на этом участке не действует ЭДС, то есть сторонними силами не совершается работа. Такой участок электрической цепи называется однородным.

Немецкий физик Г. Ом (1787-1854) экспериментально установил, что сила тока в однородном проводнике пропорциональна разности потенциалов на его концах и обратно пропорциональна сопротивлению проводника (закон Ома для участка цепи):

(2.8)

где R – электрическое сопротивление проводника, определяющее упорядоченность перемещения свободных носителей тока.

Электрическое сопротивление металлического проводника обусловлено тем, что свободные электроны при своем движении взаимодействуют (соударяются) с положительными ионами кристаллической решетки. Поэтому сопротивление проводников зависит, прежде всего, от материала проводника, то есть строения его кристаллической решетки. Для однородного цилиндрического проводника длиной l и площадью поперечного сечения S сопротивление определяется по формуле

(2.9)

где удельное сопротивление (сопротивление однородного цилиндрического проводника, имеющего единичную длину и единичную площадь поперечного сечения), характеризующее материал проводника.

Единица сопротивления – ом: 1 Ом – сопротивление такого проводника, в котором при напряжении 1 В течет постоянный ток силой 1 А.

Величина обратная сопротивлению, называется электрической проводимостью. Единица проводимости – сименс: 1 См – электрическая проводимость проводника сопротивлением 1 Ом.

Удельное электрическое сопротивление проводника зависит не только от рода вещества, но и от температуры:

(2.10)

где удельное сопротивление при 0^оС; t – температура (по шкале Цельсия); температурный коэффициент сопротивления, характеризующий относительное изменение сопротивления проводника при его нагревании на 1^о С или 1 К:

Температурные коэффициенты сопротивления веществ различны при разных температурах. Однако для многих металлов изменение с темпе ратурой невелико. Для всех чистых металлов

Закон Ома можно представить в дифференциальной форме. Подставив выражение для сопротивления (2.9) в закон Ома (2.8), получим

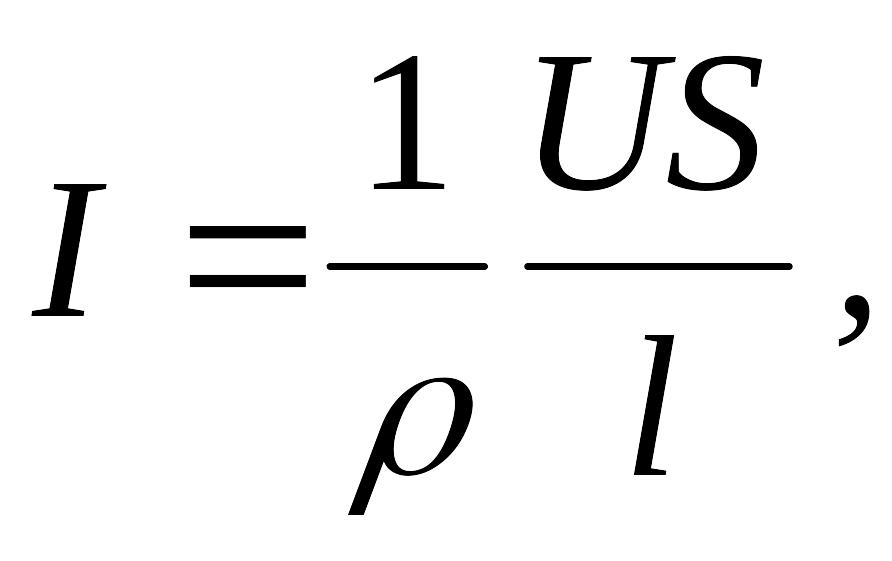
или

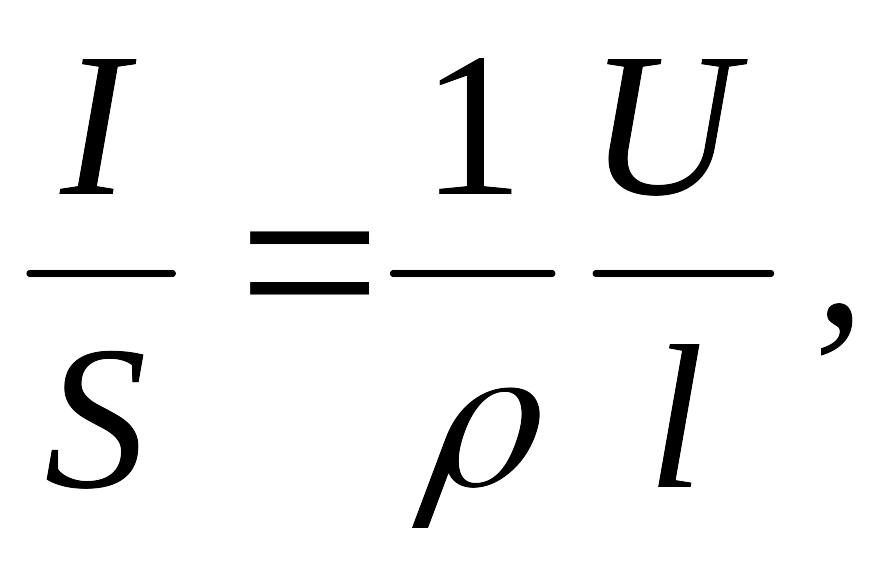
где величина называется удельной проводимостью (См/м). Учитывая, что напряженность электрического поля в проводнике, а плотность тока, последнее выражение можно записать в следующем виде:

Так как в изотропном проводнике носители тока в каждой точке движутся в направлении вектора , то направления и совпадают. Поэтому, в окончательном виде

(2.11)

Выражение (2.11) представляет собой закон Ома в дифференциальной форме, который связывает плотность тока в любой точке внутри проводника с напряженностью электрического поля в этой же точке. Это соотношение справедливо и для переменных полей.