8.Задача про призначення

Задача про призначення змістовно формулюється наступним чином. Необхідно розподілити робіт серед виконавців таким чином, щоб сумарні витрати на виконання робіт були мінімальні. Відомі витрати — на виконання i-ї роботи j-м виконавцем для всіх робіт та виконавців. Окрім того, відомо, що кожен з виконавців може виконувати не більш, ніж одну роботу, і кожна робота може виконуватись не більш, ніж одним виконавцем.

Ця задача є не чим іншим, як специфіцним випадком транспортної — роботи можна розглядати, як пункти зберігання, виконавців — як пункти споживання, запаси в кожному з пунктів зберігання та потреби в пунктах споживання рівні одиниці, тариф на перевезення — .

В залежності від початкових умов для приведення задачі до задачі закритого типу додаємо фіктивні роботи або фіктивних виконавців, і отримуємо задачу з роботами та виконавцями. Формальна постановка задачі виглядатиме наступним чином.

,

, якщо і-та робота не виконується j-м виконавцем, та 1 — якщо виконується. Слід зауважити, що розв’язок задачі про призначення завжди буде виродженим, оскільки для невиродженого розв’язку ранґ матриці коефіцієнтів С повинен становити , в той час як призначеними можуть бути робіт. Таким чином, задачу про призначення можна розв’язати за допомогою методів розв’язування транспортних задач, але при цьому необхідно буде заповнення в транспортній таблиці пустих клітинок безмежно малими перевезеннями .

В той же час виявилося можливим з врахуванням специфічних особливостей задачі про призначення побудувати ефективні алгоритми її розв’язування, одним з яких є так званий угорський алгоритм. Для обґрунтування редукції в цьому алгоритмі покажемо, що оптимальний розв’язок задачі не зміниться, якщо до будь-якого рядка чи будь-якого стовпчика додати чи відняти постійну величину. Віднімемо від кожного i-го стовпчика та кожного j-го рядка постійні для відповідного рядка чи стовпчика значення та : , = .

Таким чином ця процедура зменшує значення функції мети на постійну величину, що не приводить до зміни положення оптимального розв’язку.

Угорський алґоритм для задачі про призначення складається з наступних кроків.

Крок 1. Редукція рядків та стовпчиків матриці С.

Послідовно в кожному з рядків матриці визначаємо мінімальний елемент та зменшуємо на це значення всі інші елементи відповідного рядка. В отриманій чином матриці таку ж процедуру виконуємо з кожним стовпчиком. Метою цього кроку є отримання максимальної кількості нульових елементів в редукованій матриці.

Крок 2. Реалізація призначень.

a). Послідовно переглядаючи рядки, визначаємо ті з них, в яких знаходиться рівно по одному невикресленому нульовому елементу. В кожному з таких рядків виконуємо призначення, яке відповідає цьому невикресленому нульовому елементу (призначені нулі відзначаємо кружечками). При виконанні призначення в кожному стовпчику, який відповідає призначеному нулеві, викреслюємо всі невикреслені раніше елементи.

b). Послідовно переглядаємо стовпчики, визначаємо ті з них, в яких знаходиться рівно по одному нульовому елементу. В кожному з таких стовпчиків виконуємо призначення, що відповідає невикресленому нульовому елементу. При виконанні призначення в кожному рядкові, який відповідає призначеному нулеві, викреслюємо всі невикреслені раніше елементи.

c). Перевірка: Якщо знайдене таким чином призначення повне (тобто призначено нульових елементів), то воно й буде оптимальним розв’язком задачі — стоп. Якщо деякі з нулів не викреслені (тобто залишилися рядки та стовпчики з кількістю нулів, більшою ніж 1), то обираємо рядок чи стовпчик з мінімальною кількістю нулів, довільно призначаємо один з них, викреслюємо всі нулі в в цьому рядку (стовпчику) та відповідному стовпчикові (рядку) і далі виконуємо крок 2. Якщо викреслені та призначені всі нулі в матриці, і знайдене призначення неповне, то переходимо до кроку 3.

Крок 3. Модифікація редукованої матриці.

З метою модифікації редукованої матриці без зміни положення оптимального розв’язку виконуємо наступні дії. Відміняємо всі призначення та викреслення.

a). обчислюємо число нулів в кожному невикресленому рядку та кожному невикресленому стовпчику;

b). викреслюємо рядок чи стовпчик з максимальною кількістю нулів;

c). виконуємо a та b до того часу, поки всі нулі не будуть викреслені;

d). від всіх невикреслених елементів віднімаємо значення мінімального невикресленого елементу та додаємо його до елементів, що знаходяться на перетині викреслюючих прямих. Перейти до кроку 2.

Приклад.

Задана матриця С: Редукована за рядками матриця:

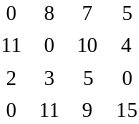
За стовпчиками: Матриця після кроку 2:

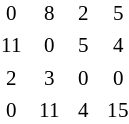
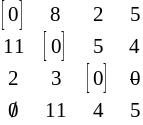
Оскільки призначення неповне, переходимо до кроку 3.

Після завершення викреслювань визначаємо зміни в елементах матриці та виконуємо крок 2 з модифікованою матрицею:

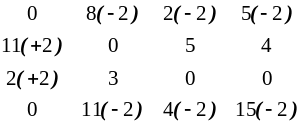
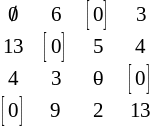
Таким чином отримане повне призначення, яке й є оптимальним розв’язком задачі про призначення. Повертаючись до умови задачі, розраховуємо оптимальне значення функції мети для призначення:

9+4+11+4=28.

Задача про призначення може розглядатися ще й в такому змістовному формулюванні. На вакантних місць претендують осіб, причому задана ефективність виконання праці кожним з претендентів на кожній посаді. Необхідно обрати таких претендентів, щоб сумарна ефективність їх функціонування була максимальною. На відміну від попередньої ця задача є задачею максимізації, яка приводиться до вище розглянутої домноженням всіх елементів матриці ефективностей на -1 та додаванням значення максимального елемента матриці умови задачі.