6.Транспортна модель з проміжними пунктами

У стандартній транспортній моделі передбачається, що прямий маршрут між пунктом виробництва і пунктом споживання є маршрутом мінімальної вартості. Так із таблиці відстаней між трьома автомобільними заводами і двома центрами розподілу утворюються найкоротші маршрути між пунктами виробництва і пунктами споживання. Це означає, що визначенню вартостей перевезень одиниці продукції в стандартній транспортній моделі повинна передувати попередня робота, пов'язана з виявленням найкоротших маршрутів.

У задачах невеликої розмірності визначення найкоротшого маршруту не складає труднощів. Коли ж число пунктів виробництва і пунктів споживання є велике, для визначення мінімальної вартості прямого перевезення одиниці продукції по конкретному маршруту варто звернутися до алгоритму знаходження найкоротшого шляху.

Інший метод визначення мінімальної вартості прямого перевезення пов'язаний із постановкою задачі як задачі з проміжними пунктами. При цьому допускається «перевезення» вантажу (частково або цілком) через інші вихідні пункти або використання пунктів призначення транзитом, перед тим, як вантаж досягне встановленого пункту призначення. У задачі з проміжними пунктами автоматично шукається маршрут мінімальної вартості між пунктом виробництва і пунктом призначення без попереднього визначення найкоротшого маршруту.

Введення проміжних пунктів дає можливість перевозити весь объем продукції з вихідних пунктів через будь-який інший вихідний пункт або пункт призначення, перед тим, як продукція буде розподілена серед споживачів. Це означає, що будь-яку вершину транспортної мережі (як вихідний пункт, так і пункт призначенні) можна розглядати як транзитний пункт. Оскільки апріорі не відомо, які вершини будуть мати цю властивість, можна сформулювати задачу таким чином, щоб кожну вершину можна було розглядати і як вихідний пункт, і як пункт призначення. Іншими словами, число вихідних пунктів (пунктів призначення) у задачі з проміжними пунктами дорівнює сумі вихідних пунктів і пунктів призначення в стандартній задачі.

Для пояснення цього зауваження розглянемо наступну задачу.

Приклад.

Є три заводи і два центри розподілу. У моделі з проміжними пунктами буде п'ять вихідних пунктів і п'ять пунктів призначення.

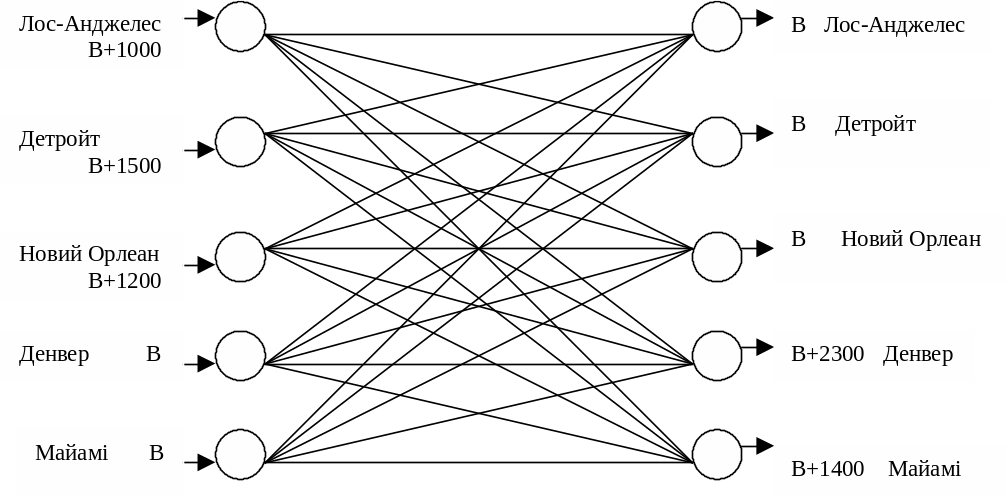
Для того щоб врахувати транзитні перевезення, у кожному вихідному пункті призначення передбачений додатковий буфер ємністю В. За визначенням ємність буфера повинна бути не менше сумарного обсягу виробництва (або попиту) стандартної (збалансованої) транспортної задачі, тобто .

Вартості в розрахунку на одиницю вантажу оцінюються на підставі даних про маршрути, що з'єднують вихідні пункти з пунктами призначення в моделі з проміжними пунктами. Очевидно, що коефіцієнти вартості перевезення між спочатку заданими вихідними пунктами і пунктами призначення залишаються такими ж, як і в попередньому прикладі. Зауважимо також, що вартість перевезення з деякого пункту в нього ж (скажемо, із Денвера в Денвер) дорівнює нулю, і вартість перевезення може змінюватися в залежності від напрямку (наприклад, маршрут Детройт - Денвер може відрізнятися по вартості від маршруту Денвер - Детройт, якщо використовуються різноманітні режими перевезень).

Т аблиця 2

	0		130		90		80		215
3700										4700
	135		0		101		100		108
		3700								5200
	95		105		0		102		68
				3500						4900
	79		99		110		0		205
						3700				3700
	200		107		72		205		0
								3700		3700
3700		3700		3700		6000		5100

У табл. наведений оптимальний розв’язок розглянутої вище задачі з проміжними пунктами, у якій місткість буфера В дорівнює 3700 автомобілів. Зауважимо, що коефіцієнти вартості перевезень між спочатку заданими вихідними пунктами (Лос-Анжелес, Детройт і Новий Орлеан) і пунктами призначення (Денвер і Майамі) ті ж, що й у прикладі. Передбачається, що інші коефіцієнти оцінюються в залежності від відстані і режиму перевезень.

Діагональні елементи отримані в результаті використання буфера. Вони не дають ніякої інформації про остаточний розв’язок. Позадіагональні елементи забезпечують одержання розв’язку, поданого на рис нижче. З Детройта до Майамі перевезення відбувається через проміжний пункт у Новому Орлеані, куди надходить 200 автомобілів. Всі інші перевезення здійснюються безпосередньо з заводів у центри розподілу.

Крім розглянутої вище можливі ситуації, при яких має місце транзитне перевезення продукції. Наприклад, у прикладі остаточні пункти призначення, куди надходять автомобілі, можуть представляти окремих продавців, а не крупні центри розподілу. З метою спрощення припустимо, що є лише п'ять продавців, що одержують свої замовлення з центрів розподілу в Денвері і Майамі. На рис. центри розподілу зображені у виді тимчасових складів, із

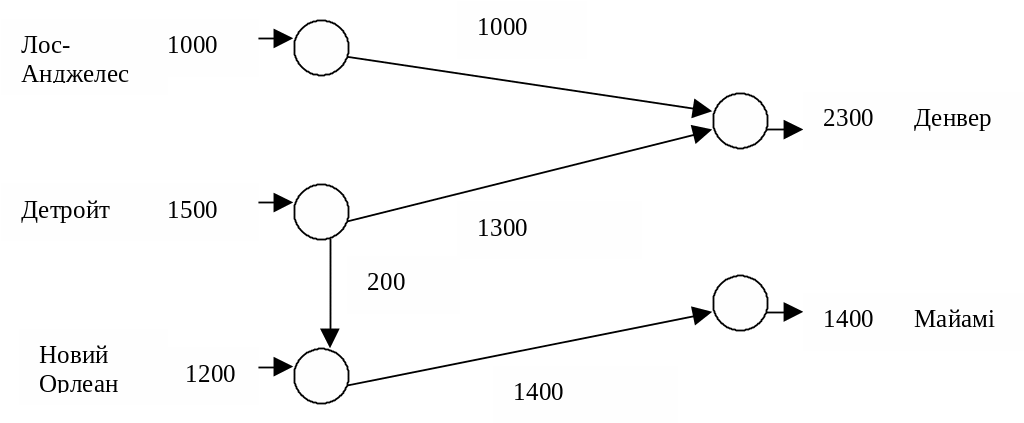
яких автомобілі потрапляють у остаточні пункти призначення. Відповідні розміри, що характеризують попит п'ятьох продавців, складають 800, 500, 750, 1000 і 650 автомобілів. Припустимо, що продавець може одержувати товар із будь-якого центру розподілу. (З прикладу очевидно, що розміри попиту в центрах розподілу

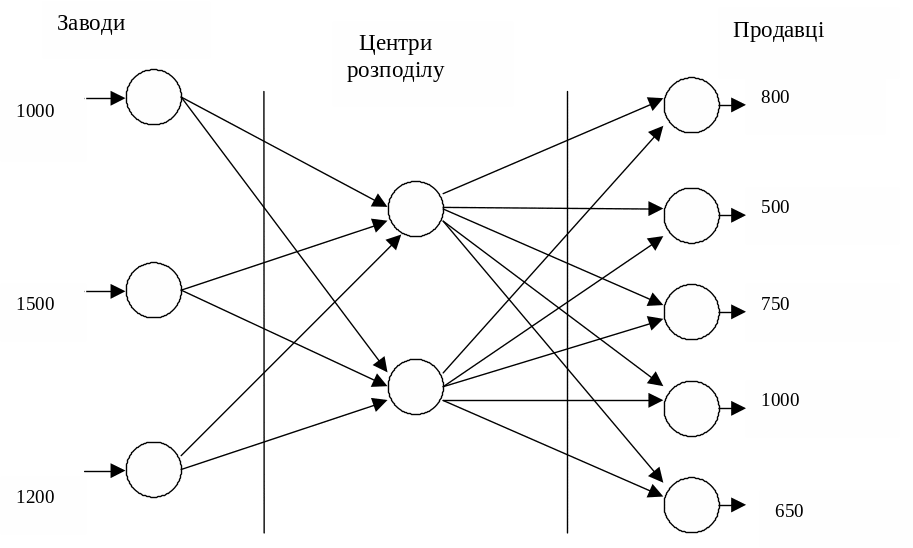
не використовуються в якості вихідної інформації. ) У даному випадку, як показано на рис., проміжними пунктами можуть бути тільки центри розподілу.

Оскільки центри розподілу (вершини 4 і 5 на рис 3.) є єдиними проміжними пунктами, кожний із них може розглядатися і як пункт призначення, і як вихідний пункт. З іншого боку, заводи грають лише роль вихідних пунктів, а продавці – пунктів призначення. Побудована з урахуванням цього модель із проміжними пунктами наведена в табл.3.

Зауважимо, що в центрах розподілу (вершини 4 і 5) ємність буфера В, рівна 3700 автомобілів, додається до відповідних розмірів обсягу виробництва і попиту. Очевидно, що ніякої буферної ємності не потрібно додавати до розміру об'єму виробництва

	4	5	6	7	8	9	10
1			X	X	X	X	X	1000
2			X	X	X	X	X	1500
3			X	X	X	X	X	1200
4								3700
5								3700
	3700	3700	800	500	750	1000	650

того або іншого заводу або величині, що характеризує попит продавців. Нагадаємо, що буфер уводиться лише в тих пунктах, що можуть розглядатися і як вихідні пункти, і як пункти призначення, тобто в ситуації, коли перевезення здійснюється через ці пункти транзитом. З рис. зрозуміло, що прямі перевезення з заводу продавцю не дозволені. У табл. 3 це обмеження подане забороненими (заштрихованими) комірками. При розв’язанні задачі забороненому маршруту відповідає дуже велика вартість , записана у відповідній комірці.

	1	2	3	4	5	6	7	8	9	10
1						X	X	X	X	X	1000
2						X	X	X	X	X	1500
3						X	X	X	X	X	1200
4											3700
5											3700
	3700	3700	3700	3700	3700	800	500	750	1000	650

Припустимо, що дозволені маршрути з проміжними пунктами між заводами і центрами розподілу. Пряме перевезення допускається лише з центру розподілу продавцям. У табл. вище подана така модель. Зауважимо, що кожний завод і центр розподілу може тепер розглядатися і як вихідний пункт, і як пункт призначення.