4.Розв’язування транспортних задач з ускладненнями в постановці

Метод потенціалів може бути застосований також до розв’язування транспортних задач з додатковими умовами. Цими додатковими умовами, або ускладненнями в постановці, можуть бути наступні:

• заборона на перевезення продукту з конкретних пунктів зберігання в конкретні пункти споживання;

• перевезення продукту з конкретного пункту зберігання в конкретний пункт споживання лише строго визначеної кількості;

• завезення з конкретного пункту зберігання в конкретний пункт споживання не менше визначеної кількості продукту;

• завезення з конкретного пункту зберігання в конкретний пункт споживання не більше визначеної кількості продукту;

У тому випадку, коли поставки з А_і в В_j не можуть бути здійснені, відповідний тариф на перевезення с_ij =M, де M — дуже велике додатнє число.

В тому випадку, коли з А_і в В_j необхідно перевезти строго d_ij одиниць продукту, це число записують у відповідну клітинку, яку надалі вважаємо вільною з тарифом M — якнайбільшим.

Якщо з пункту А_і до пункту В_j необхідно перевезти не менш, ніж а_ij продукту, то вважаємо, що запаси А_і та потреби В_j зменшені на а_ij одиниць.

Якщо з пункту А_і до пункту В_j необхідно перевезти не більш, ніж а_ij одиниць, то для кожного обмеження такого типу вводиться додатковий стовпчик: в стовпчику В_j потреби = а_ij в додатковому стовпчику потреби

b_j— а_ij , а вартість перевезення с_ij=M.

5.Інтерпретація методу потенціалів як симплекс-методу.

Метод потенціалів є не чим іншим, як варіантом симплекс—методу, що орієнтований на максимальне врахування особливостей транспортної задачі. Метод потенціалів інтерпретується як симплекс — метод наступним чином:

• заповнені клітинки транспортної таблиці (де є перевезення) відповідають базовим змінним, а їх значення — значенням базових змінних, а не заповнені — небазовим змінним;

• знаходження клітинки, що буде заповнюватися, відповідає пошуку змінної, що вводитиметься до бази;

• знаходження клітинки в циклі, відміченої знаком “—“ з найменшим значенням перевезення, відповідає пошуку змінної, що виключатиметься з бази;

• переміщення перевезення в межах циклу відповідає переходу до нової симплекс-таблиці в симплекс-методі;

• для включення в базу в симплекс-методі обирається змінна з найбільшим за абсолютною величиною від’ємним значенням 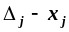, а в транспортній задачі — незаповнена клітинка з найбільшим додантім значенням потенціалу (транспортна задача — це задача на знаходження мінімуму);

• значення потенціалів незаповнених клітинок (небазових змінних) в транспортній задачі відповідають коефіцієнтам 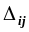у Q-рядку симплекс-таблиці (за умови відповідної переіндексації змінних);

• потенціали рядків та потенціали стовпчиків в транспортній таблиці відповідають значенням змінних двоїстої задачі; знаючи значення двоїстих змінних, на кожній ітерації визначається як різниця між правою та лівою частиною відповідного обмеження двоїстої задачі;

• теорема про потенціали є не чим іншим, як видозміною теореми про доповнюючу нежорсткість (другої теореми двоїстості).

Розглянемо транспортну задачу з двома пунктами зберігання та трьома пунктами споживання в загальному вигляді:

c₁₁x₁₁ + c₁₂x₁₂ + c₁₃x₁₃ + c₂₁x₂₁ + c₂₂x₂₂ + c₂₃x₂₃  Min

x₁₁ + x₂₁ = b₁ 

x₁₂ + x₂₂ = b₂ 

x₁₃ + x₂₃ = b₃ 

x₁₁ + x₁₂ + x₁₃ = a₁ 

x₂₁ + x₂₂ + x₂₃ = a₂ 

Позначимо двоїсті змінні, що відповідають обмеженням на пункти споживання (потреби кожного пункту споживання повинні бути задовольнені), як , а двоїсті змінні, що відповідають обмеженням на пункти зберігання (весь продукт, що знаходиться на кожному пункті зберігання, повинен бути перевезений), як . Помножимо ліву та праву частину кожного з рівнянь прямої задачі на -1 та поміняємо знак у функції мети — щоб отримати канонічну форму задачі. Будуючи двоїсту до неї, отримаємо:

+ <= c₁₁

+ <= c₁₂

+ <= c₁₃

+ <= c₂₁

+ <= c₂₂

+ <= c₂₃

Таким чином, для закритої транспортної задачі в загальному вигляді

,

двоїста буде наступною:

.

Позначимо та застосуємо результати теорем двоїстості. Дійсно, значення критеріїв оптимальності рівне різниці між лівою та правою частинами відповідного обмеження двоїстої задачі, і у випадку, коли змінна прямої задачі є базовою, значення , і розв’язок є оптимальним, коли , оскільки пряма задача є задачею мінімізації. Таким чином якщо в якомусь розв’язку транспортної задачі для базових змінних x_ij — , а для небазових — , то цей розв’язок є оптимальним — що й доводить теорему про потенціали. Таким чином метод потенціалів є варіантом симплекс-методу, який враховує специфіку транспортної задачі і працює ефективно. Однак у випадку виродження розв’язування задачі ускладнюється.

Опорний план (базовий розв’язок) називається виродженим, якщо число заповнених клітинок в таблиці менше за , тобто рангу матриці обмежень транспортної задачі. Вироджений опорний план може виникнути як на початку розв’язку — коли вироджений початковий базовий розв’язок, або при переході від одного до наступного опорного плану.

Якщо вироджений початковий опорний план, то обираємо деякі нульові елементи матриці обмежень (кількістю ) в якості базових, заміняємо їх на довільні, безмежно малі перевезення так, щоб при цьому не порушилась умова опорності (відсутність циклу з ненульових перевезень — тобто лише з базових змінних). Задачу розв’язуємо як невироджену, пишучи в оптимальному плані замість нулі.

Вироджений план може бути отриманий також у випадку, якщо до циклу входить не менш, ніж два мінімальні елементи зі знаком “—“ в клітинках. В цьому випадку вважають нульовим лише один з цих елементів, інші такі в процесі руху циклом заміняємо на та продовжуємо розв’язувати задачу як невироджену. Якщо на деякому кроці обраний для виведення з бази елемент зі значенням перевезення , то значення функції мети не змінюється, а перевезення для елементу, що вводиться до бази, буде .