3.Метод потенціалів для знаходження оптимального розв’язку транспортної задачі

Метод потенціалів є особливим випадком симплекс-методу, що враховує особливості транспортної задачі. Метод потенціалів ґрунтується на наступній теоремі.

Теорема про потенціали.

Якщо для деякого опорного плану , транспортної задачі існують такі числа що при , при для всіх , то — оптимальний план транспортної задачі.

Величини та називаються потенціалами пунктів постачання та пунктів споживання відповідно.

Алгоритм методу потенціалів включає наступні кроки.

1. Розраховуємо значення потенціалів рядків та стовпців та , розв’язуючи систему рівнянь , що складені для заповнених клітинок транспортної задачі. Число заповнених клітинок дорівнює , а система має невідомих, тому для визначеності приймаємо та послідовно з рівнянь знаходимо інші значення та .

2. Для кожної з вільних клітинок розраховуємо значення 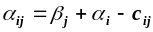. Якщо 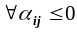, то план оптимальний. В іншому випадку обираємо максимальне значення 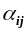та заповнюємо відповідну клітинку, змінюючи об’єми поставок в інших заповнених клітинках, що пов’язані з нею циклом.

а). Побудова циклу.

Цикл будується у вигляді ламаної лінії в таблиці транспортної задачі, вершини якого розташовані в заповнених клітинках таблиці, а ланки ламаної — вздовж рядків та стовпчиків, причому в кожній вершині циклу зустрічається рівно дві ланки — одна з них проходить вздовж стовпчика, а інша — вздовж рядка. Точки самоперетину ламаної не є вершинами. Однією з вершин циклу є обрана незаповнена клітинка.

б). Переміщення перевезень в межах клітинок, пов’язаних з вільною циклом.

Починаючи з вільної клітинки, якій приписується знак +, іншим почергово, просуваючись за циклом, приписуємо знаки — та +.

В вільну клітинку переносимо найменше з чисел , що знаходиться в мінусових клітинках. Це число додається до клітинок зі знаком + та віднімається від клітинок зі знаком — . В результаті вільна клітинка стає заповненою, а заповнена з мінімальним значенням та +-ом — вільною. Баланс перевезень не змінюється, оскільки в кожному стовпчику та рядку додається і віднімається одне й те ж значення.

Перехід до кроку 1.

Нижче наведені приклади можливих конфіґурацій циклів в транспортній таблиці.

Приклад.

На трьох пунктах зберігання наявні наступні запаси: a1=100, a2=150, a3=50. Потреби чотирьох пунктів споживання становлять b1=75, b2=80, b3=60, b4=85. Вартості перевезень одиниці продукції задані матрицею С 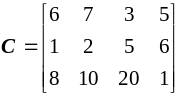. Прямою перевіркою впевнюємося, що задача закритого типу, оскільки сумарні потреби рівні сумарним запасам. Застосуємо на першому кроці для знаходження початкового опорного розв’язку метод північно-західного кута.

	B1	B2	B3	B4	Зап.
A1	6 75	7 25	3	5	100
A2	1	2 55	5 60	6 35	150
A3	8	10	20	1 50	50
Потр.	75	80	60	85	300

Розраховуємо значення потенціалів рядків та стовпчиків, використовуючи для цього заповнені клітинки таблиці та присвоюємо значення потенціалу .

	6	7	10	11
0	6 75	7 25	3	5
-5	1	2 55	5 60	6 35
-10	8	10	20	1 50

Після цього розраховуємо потенціали незаповнених клітинок і будуємо цикл. Оскільки серед потенціалів незаповнених клітинок є додатні, то знайдений опорний розв’язок не оптимальний — клітинка з найбільшим позитивним значенням потенціалу обирається як вершина циклу, а всі інші клітинки — вершини циклу повинні бути заповненими.

	6		7		10		11
0	6		7	-	3	+	5
		75		25		7		6
-5	1		2	+	5	-	6
		0		55		60		35
-10	8		10		20		1
		-12		-13		-20		50

Здійснюємо переміщення перевезення 25 в межах циклу та переходимо до нової транспортної таблиці з повторенням розрахунків.

	6		0		3		4
0	6	-	7		3	+	5
		75		-7		25		-1
2	1	+	2		5	-	6
		7		80		35		35
-3	8		10		20		1
		-5		-13		-20		50

Процес побудови циклу повторюємо, так як оптимального розв’язку ще не досягнуто.

	6		7		3		11
0	6	-	7		3		5	+
		40		0		60		6
-5	1	+	2		5		6	-
		35		80		-7		35
-10	8		10		20		1
		-12		-13		-17		50

В процесі переходу від однієї таблички до іншої зберігається опорність знайденого перевезення, та зменшується його сумарна вартість, тобто йде процес наближення до оптимуму. Переходимо до наступної таблиці.

	6		7		3		5
0	6		7		3		5
		5		0		60		35
-5	1		2		5		6
		70		80		-7		-6
-4	8		10		20		1
		-6		-7		-21		50

Оскільки серед потенціалів незаповнених клітинок немає ні одного додатнього, то знайдений план перевезень є оптимальним. Сумарна вартість перевезень для нього становитиме

.