Тема 1.Транспортна задача лінійного проґрамування.

1. Математична та змістовна постановка транспортної задачі.

2. Методи знаходженння початкового (опорного) плану транспортної задачі.

3. Метод потенціалів.

4. Розв’язування транспортних задач з ускладненнями в постановці.

5. Транспортна модель з проміжними пунктами

6. Інтерпретація методу потенціалів як симплекс-методу.

7. Метод диференційних рент.

8. Задача про призначення.

1.Математична та змістовна постановка транспортної задачі

Змістовно транспортна задача формулюється наступним чином. Необхідно перевезти однорідний продукт з пунктів зберігання (комор) в пункти споживання таким чином, щоб загальна вартість перевезень була мінімальною. Наявно m пунктів зберігання A₁,...,A_m та n пунктів споживання B₁,...,B_n. Запас продукту в кожному i-му пункті зберігання A_i становить а_і, а потреби в кожному j-му пункті споживання B_j рівні b_j. Вартість перевезення одиниці продукту з кожного i-го пункту зберігання в кожний j-й пункт споживання також відома і становить с_ij. Якщо сумарні потреби рівні сумарним запасам продукту в коморах — — то транспортна задача є задачею закритого типу, формальна математична модель якої виглядає наступним чином:

, , , , .

Для відкритої транспортної задачі характерним є те, що сумарні запаси та сумарні потреби є незбалансованими. Відкрита задача завжди приводиться до закритої за допомогою наступних підстановок.

В випадку, коли , тобто наявні запаси перевищують потреби, необхідно ввести додатковий пункт споживання , потреби якого становитимуть та вартості перевезень в цей пункт становитимуть . В іншому випадку , і необхідно ввести додатковий пункт зберігання з запасом та нульовими вартостями перевезень .

Для розв’язування транспортна задача завжди повинна бути приведена до задачі закритого типу. Основними властивостями закритої транспортної задачі є наступні.

1. Закрита транспортна задача завжди має припустимий розв’язок.

Для доведення припустимості закритої транспортної задачі розглянемо наступний розв’язок: , . Для цього розв’язку виконуються обмеження задачі — , , . Таким чином для закритої транспортної задачі завжди існує хоча б один припустимий розв’язок. Окрім того, розв’язок транспортної задачі не є необмеженим, тобто функція мети приймає скінчене значення, що є наслідком обмеженості многогранника — області припустимих розв’язків, так як справедливе співвідношення .

2. Ранґ матриці системи обмежень-рівностей закритої невиродженої транспортної задачі .

Матриця коефіцієнтів обмежень транспортної задачі за умови приведення задачі до класичного вигляду задачі лінійного програмування з впорядкуванням змінних в загальному випадку має вигляд:

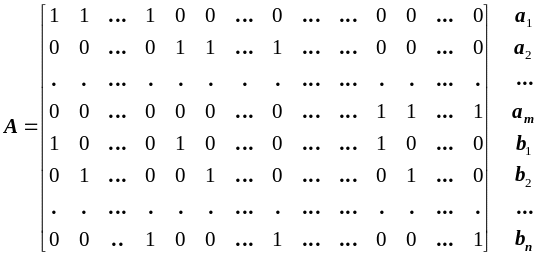
Доведемо, що ранг матриці А рівний .

1-й рядок цієї матриці є лінійною комбінацією інших: додамо поелементно рядки цієї матриці, починаючи з -го до -го та віднімемо від отриманого результату суму рядків від 2-го до -го — отримаємо 1-й рядок. Таким чином ми показали, що . Доведемо тепер, що рядки від 2-го до -го є лінійно незалежними. Для цього слід показати, що будь який з цих рядків представляється лінійною комбінацією інших лише за умови рівності нулю всіх лінійних коефіцієнтів.

Помножимо 2-й рядок матриці на , і так далі -й — на , -й — на ,..., -й — на , додамо їх, і припустимо, що значення суми рівне нулю. Тоді для перших координат цього нульового рядка отримаємо рівності

......................................................................................

......................................................................................

.

Звідси .

Для інших з -го до до -го отримаємо

..........................................................................................

Враховуючи, що , отримаємо , тобто рядки матриці А з 2-го по -й є лінійно незалежними і .

3. Якщо значення всіх коефіцієнтів в транспортній задачі закритого типу є цілими числами — то й оптимальний розв’язок є цілочисельним, що безпосередньо випливає з унімодулярності матриці А (в кожному стовпчику є по два одиничних елементи, а інші рівні нулю). З іншого боку — на кожній ітерації методу потенціалів перевезення змінюються на ціле число, і крім того початковий опорний план є також цілочисельним.

Алгоритм розв’язування транспортної задачі складається з двох основних етапів:

1. Знаходження початкового опорного плану транспортної задачі (початкового базового розв’язку).

2. Покрокове покращення плану перевезень до моменту досягнення оптимального.