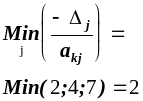4. Економічна інтерпретація задач лінійного програмування

Розглянемо пряму та двоїсту задачі ЛП:

Пряма задача:

, .

Двоїста задача:

, .

Пряму задачу розглядатимемо, як задачу виробництва певної продукції за умови наявності певних обмежених ресурсів, що можуть витрачатися на їх виробництво. Проблема полягає в тому, щоб отримати максимальний прибуток від реалізації продукції, тобто необхідно визначити кількості продуктів, які забезпечуватимуть максимальне значення функції мети.

В цій інтерпретації:

індекс видів ресурсів, що застосовуються для виробництва всіх продуктів;

індекс видів продуктів, що можуть продукуватися;

кількість продукції го типу, яка випускається;

прибуток від реалізації одиниці го продукту;

величина запасу го ресурсу;

кількість го ресурсу, що витрачається на виробництво одиниці го продукту;

прибуток від реалізації продукції.

Коефіцієнт при змінній в рядку прямої задачі

Різниця між лівою та правою

частинами обмеження двоїстої

задачі, яке асоційоване з цією

початковою змінною

=

Для подальшого аналізу використаємо результати теорем двоїстості, власне співвідношення , тобто змістовно

а також рівність значень функцій мети для прямої та двоїстої задачі в оптимальній точці.

Використаємо співвідношення для змістовної інтерпретації змінних двоїстої задачі. Перепишемо це співвідношення у вигляді і визначимо розмірність y:

.

Звідси розмірність змінних двоїстої задачі: , тобто є цінністю ресурсу (його тіньовою ціною). Для неоптимального розв’язку , тобто (прибуток)<=(цінність ресурсу), іншими словами цінні ресурси не використані повністю, і можливе збільшення прибутку за рахунок використання відповідних видів виробничої діяльності (випуску продукції певних видів).

Обмеження двоїстої задачі можна записати у вигляді: , де змістовно сумарна оцінка ресурсів, що витрачаються на виробництво одиниці j-го продукту, і таким чином,

.

Тобто, якщо , то відповідний вид виробничої діяльності повинен бути введений в базу (з випливає, що ).

5. Двоїстий симплекс-метод

При розв’язуванні прямої задачі на довільній ітерації значення коефіцієнта в -рядку симплекс-таблиці дорівнює різниці між лівою та правою частинами відповідного обмеження двоїстої задачі:

.

Якщо , то , іншими словами, коли розв’язок прямої задачі неоптимальний, то розв’язок двоїстої неприпустимий. З іншого боку, якщо , то , тобто оптимальному розв’язкові прямої задачі відповідає припустимий розв’язок двоїстої.

В двоїстому симплекс-методі спочатку отримуємо розв’язок “кращий, ніж оптимальний” (надоптимальний), але неприпустимий. Двоїстий СМ забезпечує виконання умови оптимальності та наближення кожного наступного біжучого розв’язку до області припустимих розв’язків. В момент, коли отриманий розв’язок виявляється припустимим, процес розв’язування закінчується, так як останній розв’язок є оптимальним і припустимим.

Всі значення , і це співвідношення зберігається на кожній ітерації двоїстого СМ. Деякі елементи стовпчика є від’ємними. Перехід від одного біжучого розв’язку до іншого здійснюється до моменту, поки з не будуть виключені від’ємні елементи.

Алгоритм двоїстого СМ включає наступні кроки:

1. Знаходження початкового надоптимального розв’язку.

2. Перевірка біжучого надоптимального розв’язку на припустимість (Якщо в стовпчику відсутні від’ємні значення, то знайдений оптимальний розв’язок. Стоп. ).

3. Обираємо найбільше за абсолютною величиною від’ємне значення в стовпчикові і визначаємо його індекс — 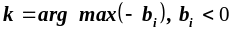— цим шляхом визначаємо змінну 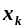, яку виключаємо з бази. Визначаємо індекс змінної, що включається до бази, 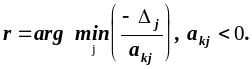Таким чином ведучий елемент є .

4. Переходимо до наступного надоптимального розв’язку так само, як і в звичайному СМ, використовуючи схему Ґауса-Жордана.

Приклад.

- 4x₁- 7x₂ - 8x₃ - 5x₄  Max,

x₁+ x₂ +2x₄ >=4 x₁+ x₂ +2x₄ - x₅ >=4

2x₁+ x₂ +2x₃ >=2 2x₁+ x₂ +2x₃ - x₆ >=2

x₁>=0 x₂ >=0 x₃ >=0 x₄>=0.

			c1	c2	c3	c4	c5	c6
xb	cb	P0	-4	-7	-8	-5	0	0
			P1	P2	P3	P4	P5	P6
x5	0	-4	-1	-1	0	-2	1	0
x6	0	-6	-2	-1	-2	0	0	1
Q		0	4	7	8	5	0	0
x5	0	-1	0	-1/2	1	-2	1	½
x1	-4	3	1	½	1	0	0	-1/2
Q		-2	0	5	4	5	0	2
x4	-5	½	0	¼	-1/2	1	-1/2	-1/4
x1	-4	3	1	½	1	0	0	-1/2
Q		-29/2	0	2	13/2	0	5/2	13/4