9. Розв‘язування системи двох нелінійних рівнянь

Задача взагалі є значно складнішою від попередньої в теоретичному плані. Ми розглянемо доволі простий приклад системи двох рівнянь та проілюструємо можливий варіант її розв’язку.

Приклад. Розв‘язати систему двох рівнянь стосовно невідомих :

У робочому листі виконання може бути таким.

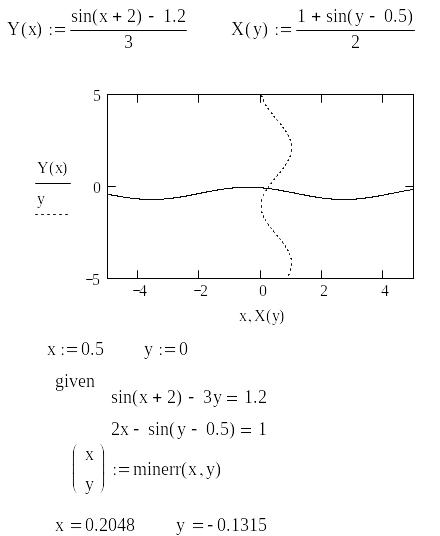
Прокоментуємо його. Спочатку проводимо графічне дослідження, для цього з першого рівняння побудуємо графік , а з другого . Після елементарних перетворень, записавши невідомі змінні як функції, маємо:

,

.

Для того, щоб програма розрізняла в одному рівнянні як аргумент, а в іншому як функцію при уведенні на робочому столі використовуємо відповідно малі та великі букви алфавіту. Після цього будуємо графіки отриманих залежностей і шукаємо наближено точку перетину функцій. Таке дослідження зручно провести змінюючи межі аргументів на координатних осях.

Для безпосереднього розв’язання задаємо початкові наближені значення 0,5, 0, записуємо службове слово given та систему рівнянь, в якій уживаємо знак логічної рівності. Функція minerr використовує метод найменших відхилень, її відповідно можна замінити на функцію методу простої ітерації find.

Завдання 3. Дослідити нелінійне рівняння графічно та знайти його корені

а) ; б) ;

в) ; г) ;

д) ; е) ;

є) ; ж) ;

з); и) ;

10. Організація обчислень з розгалуженнями

Вище для побудови таблиці значень функції чи її графічного зображення ми використовували функції , та інші, в яких змінна в дужках є формальним параметром. В процесі обчислень йому присвоювали конкретні числові значення і отримували значення самої функції. У випадку обчислювальних процесів з розгалуженнями, наприклад, , запис функції можна виконати лише з використанням програми–функції. У робочому листі це може виглядати так:

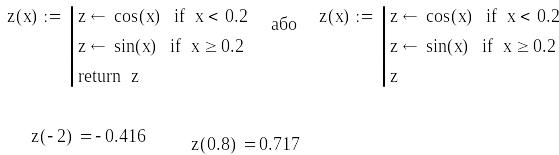
З апис програми можна виконати лише використовуючи палітру програмування, яка викликається кнопкою . Набираємо в робочому листі і клацаємо мишкою на , отримуємо і заповнюємо відповідні пусті мітки. Добавлення пустих міток робимо натиском . Значок у програмі виконує функцію оператора присвоєння (:=) і його уводимо з панелі.

Умовний оператор if використовується лише в тілі програми і для його уведення клацаємо на відповідній однойменній кнопці , отримуємо та заповнюємо мітки. Схема роботи оператора if стандартна:

оператор if умова

якщо умова приймає значення ”правда” (true), то в нашому випадку оператор присвоєння виконується, а якщо умова приймає значення ”неправда” (false), то оператор присвоєння пропускається. В свою чергу умова може бути складною, тобто складатись з багатьох простих операторів об’єднаних знаками логічних операцій (логічні додавання, множення та ін.).

Приклад. Записати програму обчислення значення функції

Лист виконання з палітрами, які при цьому використовувалися

Сама програма може бути записана і без формальних параметрів, але тоді значення необхідно задавати вище чи лівіше від неї.

Програмування відкриває ширші можливості для математичного моделювання найрізноманітніших процесів та явищ, проведення складних ітераційних обчислень, розв‘язку задач оптимізації тощо.