
- •Кафедра обчислювальної математики
- •Методичні вказівки
- •1. Література
- •1 . Дьяконов в. П., Абраменкова и. В. MathCad 7 в математике, в физике и в Internet. – м.: Нолидж., 1998. – 352 с.
- •2. Програма MathCad
- •3. Меню програми
- •Вікно програми
- •4. Робочий документ
- •5. Прийоми роботи з MathCad
- •6. Ранжовані змінні. Табулювання функцій
- •7. Розв‘язування систем лінійних алгебричних рівнянь
- •8. Розв‘язування нелінійних рівнянь
- •9. Розв‘язування системи двох нелінійних рівнянь
- •10. Організація обчислень з розгалуженнями
- •11. Задачі на обробку елементів масиву
7. Розв‘язування систем лінійних алгебричних рівнянь
У цьому параграфі розглянемо приклади розв’язування системи лінійних рівнянь за допомогою програми MathCAD, опускаючи питання існування розв’язку, його збіжності, тощо.
Розглянемо
систему
![]() лінійних алгебричних рівнянь стосовно
невідомих
лінійних алгебричних рівнянь стосовно
невідомих
![]() :
:
![]()
У
матричному вигляді систему рівнянь
можна записати як
![]() ,
де
,
де
 ,
,
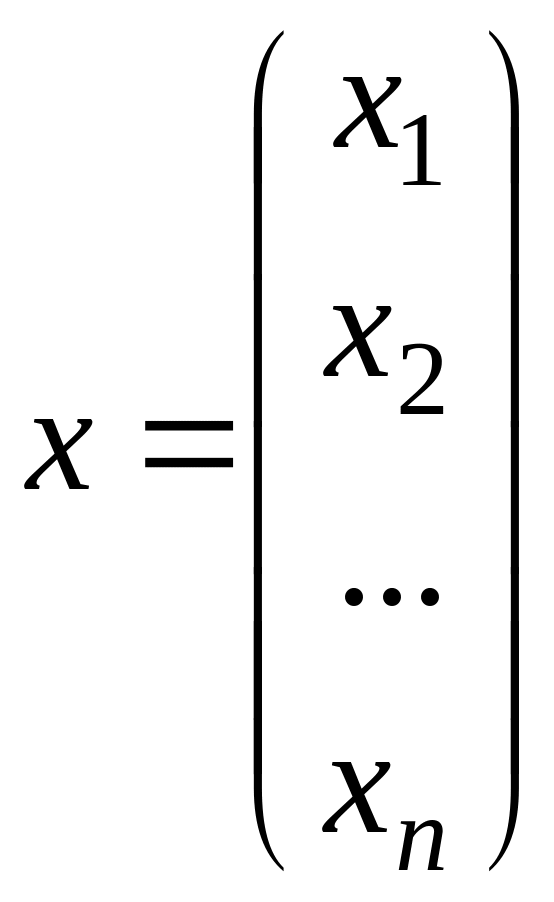 ,
,
 .
.
Нижче
подано фрагмент робочого листа розв‘язку
системи трьох рівнянь з трьома невідомими
![]()
![]() з використанням внутрішньої функції
MathCAD
з використанням внутрішньої функції
MathCAD
![]() .
.
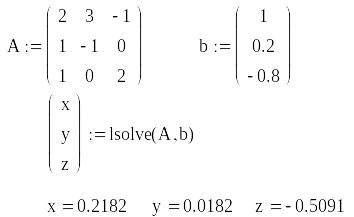
Для
уводу значень матриці A
та
вектора b
використовуємо палітру векторів і
матриць
![]() панелі
панелі
![]() . Набираємо
. Набираємо
![]() та натискаємо
та натискаємо
![]() . У вікні, що з’явиться вибираємо
кількість рядків та стовпців матриці
(3; 3), для вектора (1; 3). Отриману форму
заповнюємо даними
. У вікні, що з’явиться вибираємо
кількість рядків та стовпців матриці
(3; 3), для вектора (1; 3). Отриману форму
заповнюємо даними
 . Функцію
вибираємо із переліку після натиску
кнопки
. Функцію
вибираємо із переліку після натиску
кнопки
![]() .
Розв’язок тієї ж системи рівнянь з
використанням оберненої матриці може
мати такий вигляд:
.
Розв’язок тієї ж системи рівнянь з
використанням оберненої матриці може
мати такий вигляд:
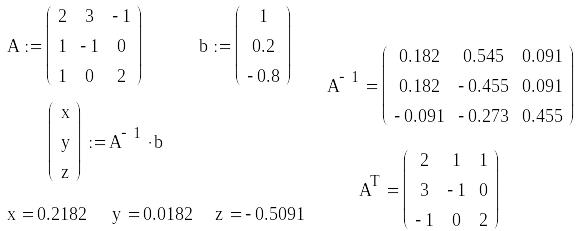
Тут
ще додатково обчислили матрицю
![]() обернену до
обернену до
![]() та транспоновану
та транспоновану
![]() .
.
Наступний спосіб, що використовує метод простої ітерації, виглядатиме так:
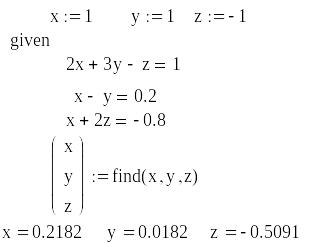
Тут
необхідно задавати початкові значення
невідомих змінних, наприклад
![]() ,
,
![]() ,
,
![]() ,
а службові слова given
та Find
набираємо з клавіатури. При записі
системи рівнянь на робочому листі знак
”=” беремо не з клавіатури, а з панелі
відношень
,
а службові слова given
та Find
набираємо з клавіатури. При записі
системи рівнянь на робочому листі знак
”=” беремо не з клавіатури, а з панелі
відношень
![]() ,
тобто використовуємо знак логічної
рівності
,
тобто використовуємо знак логічної
рівності
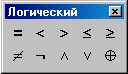 (це обов’язкове). Метод не вимагає
точного розташування змінних у записі
системи
рівнянь
на
листі.
(це обов’язкове). Метод не вимагає
точного розташування змінних у записі
системи
рівнянь
на
листі.
Замість
функції
![]() можна використати функцію
можна використати функцію
![]() ,
що має аналогічну дію і реалізує при
розв’язку системи рівнянь метод
найменших відхилень.
,
що має аналогічну дію і реалізує при
розв’язку системи рівнянь метод
найменших відхилень.
Зауважимо, що увід елементів векторів, матриць можна виконати і інакше, наприклад:

Змінним, яким числові значення не задані, по замовчуванню присвоюються нульові значення.
Завдання 2. Розв’язати систему рівнянь Dx=b наведеними вище способами, знайти її визначник, обернену та транспоновану матриці.
а)
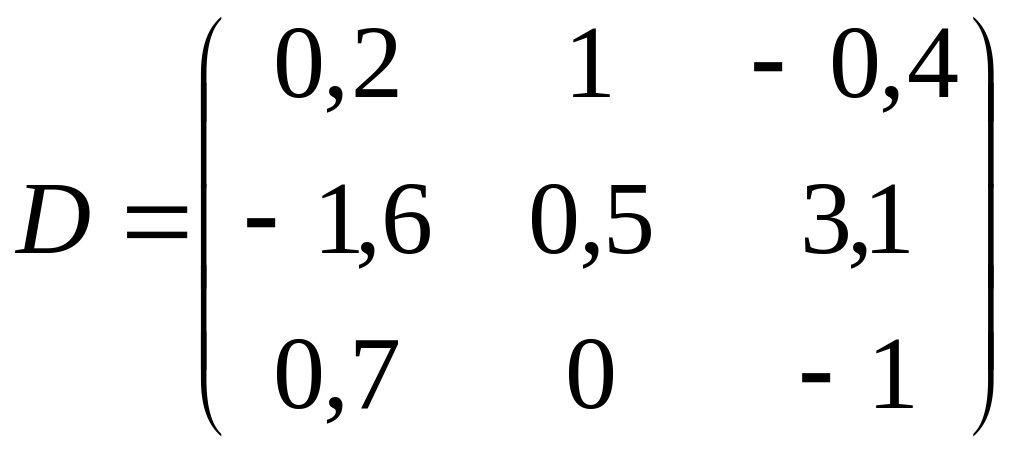 ,
,
 ; б)
; б)
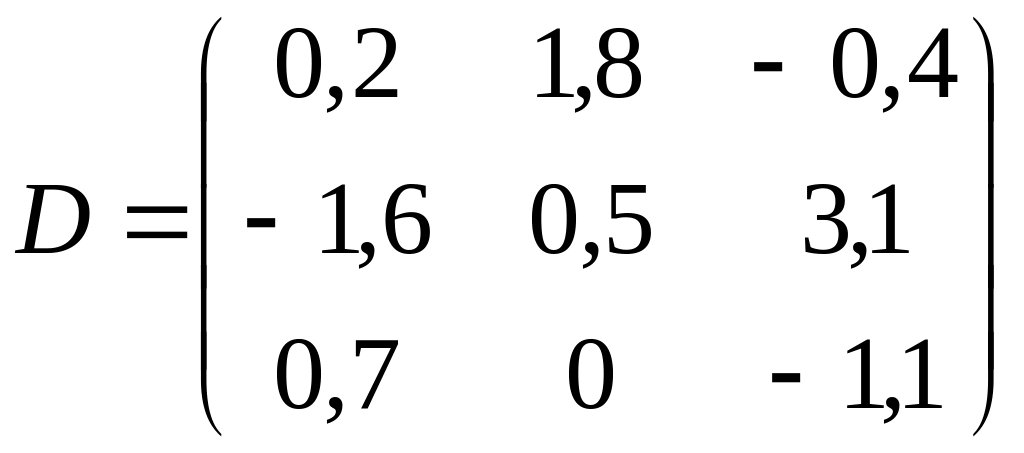 ,
;
,
;
в)
,
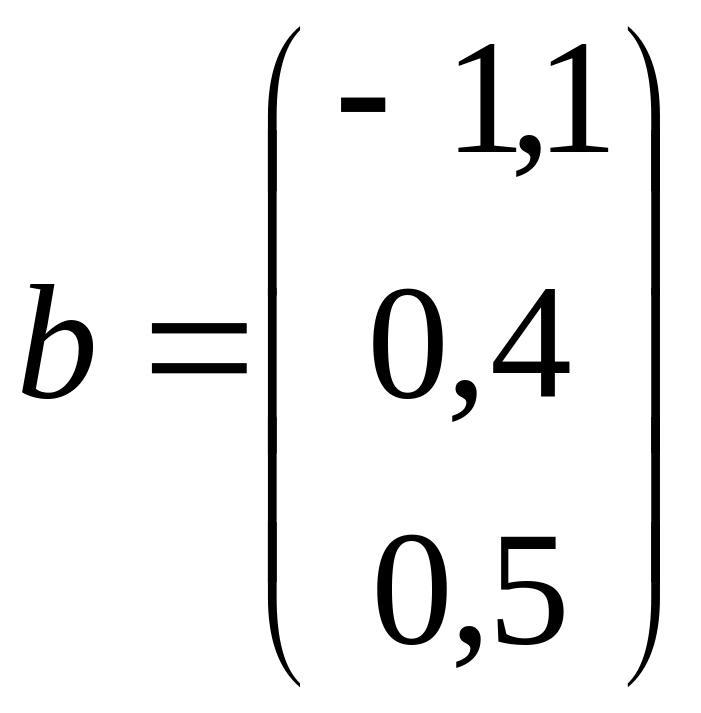 ; г)
; г)
 ,
;
,
;
д)
,
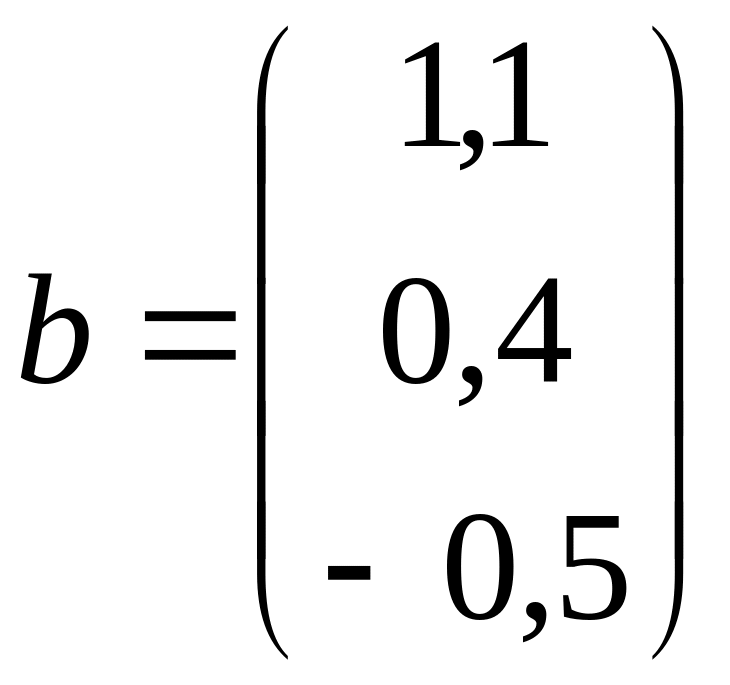 ; е)
,
; е)
,
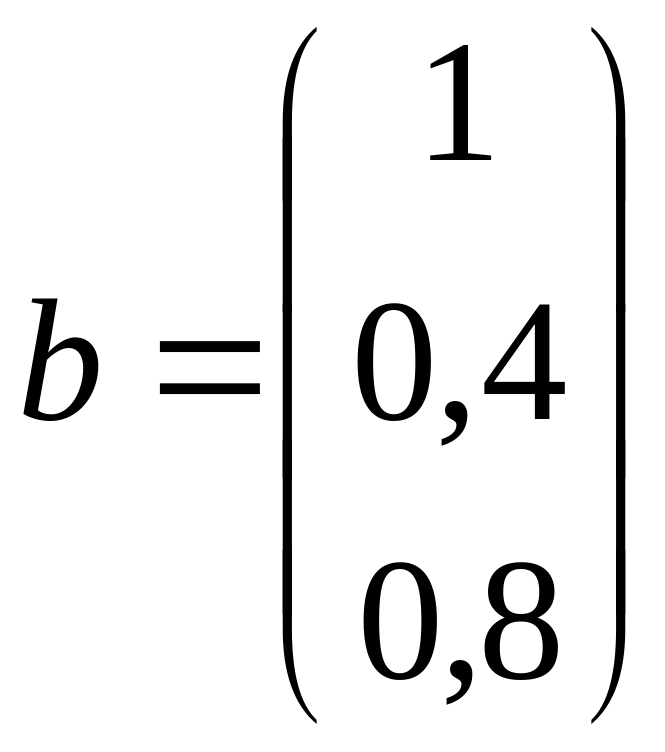 ;
;
є)
 ,
; ж)
,
; ж)
 ,
;
,
;
з)
,
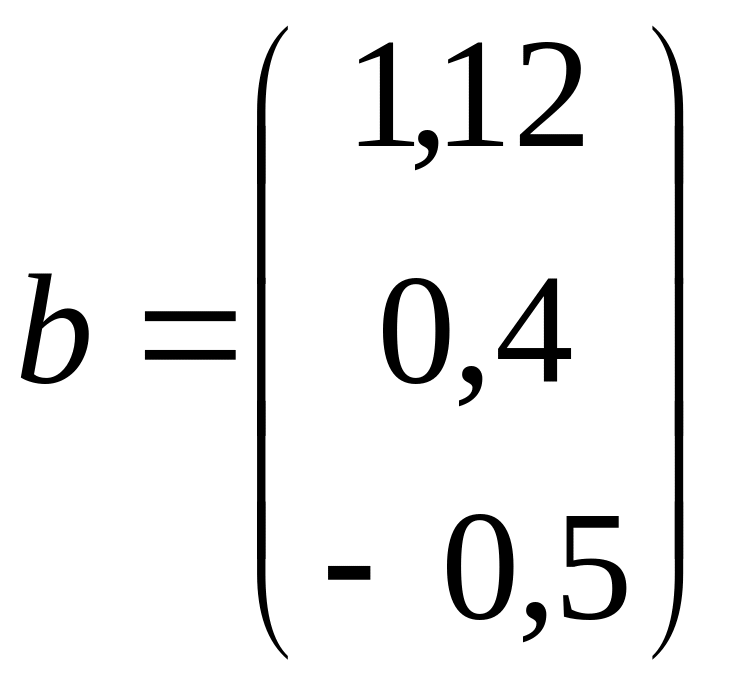 ; и)
,
; и)
,
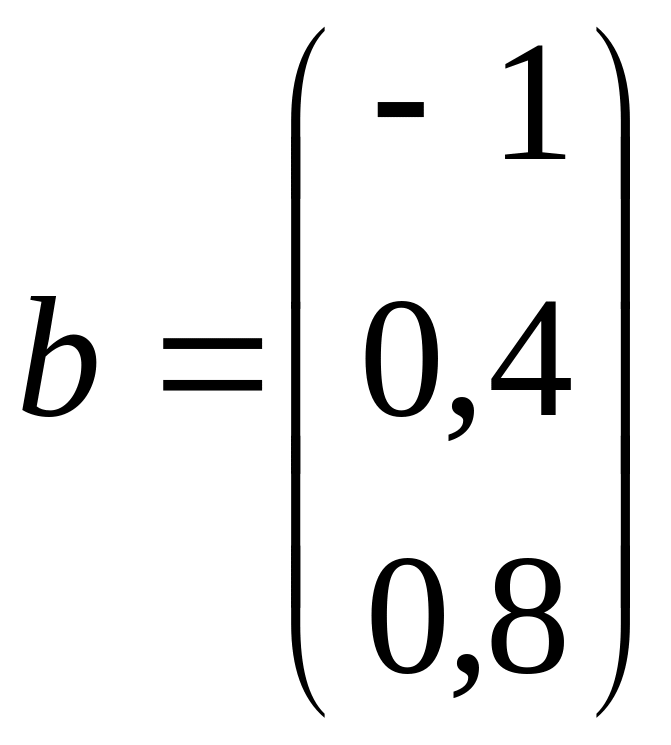 ;
;
і)
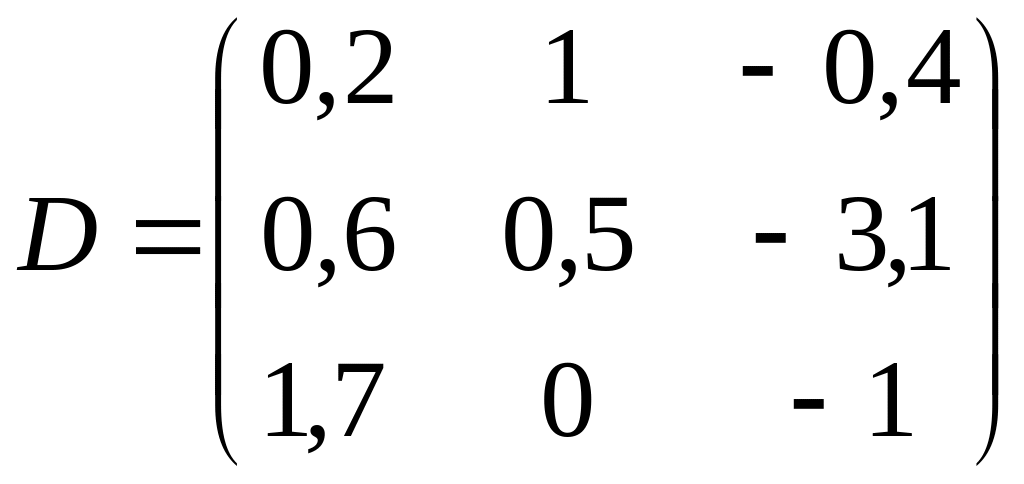 ,
,
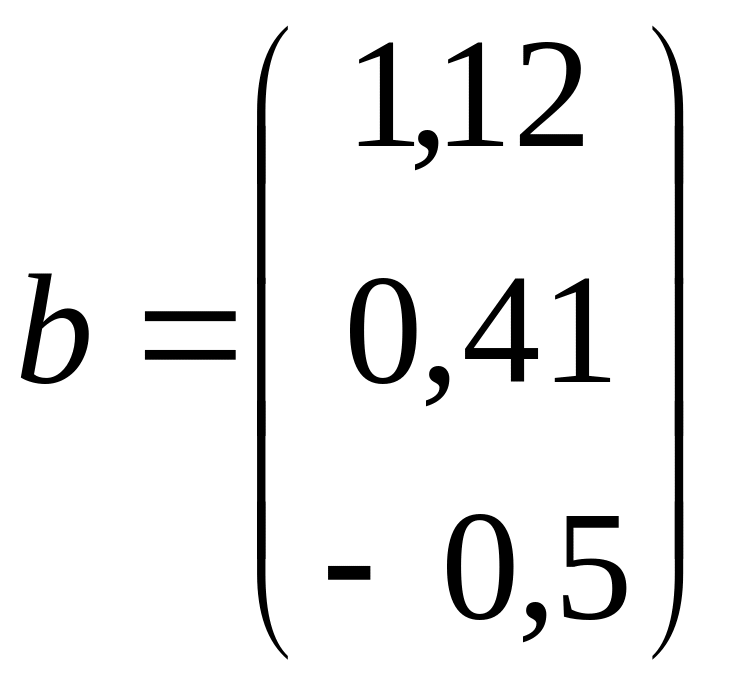 ; к)
; к)
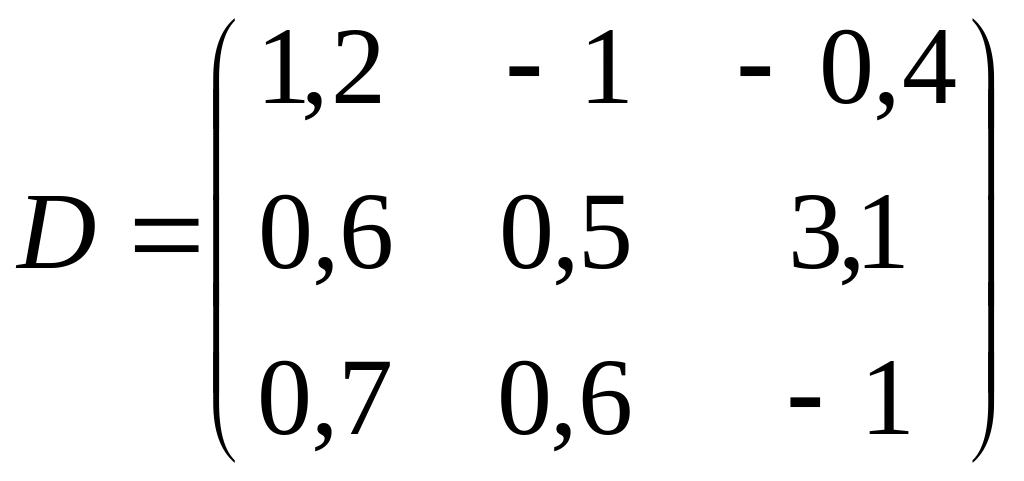 ,
,
 ;
;
л)
 ,
; м)
,
; м)
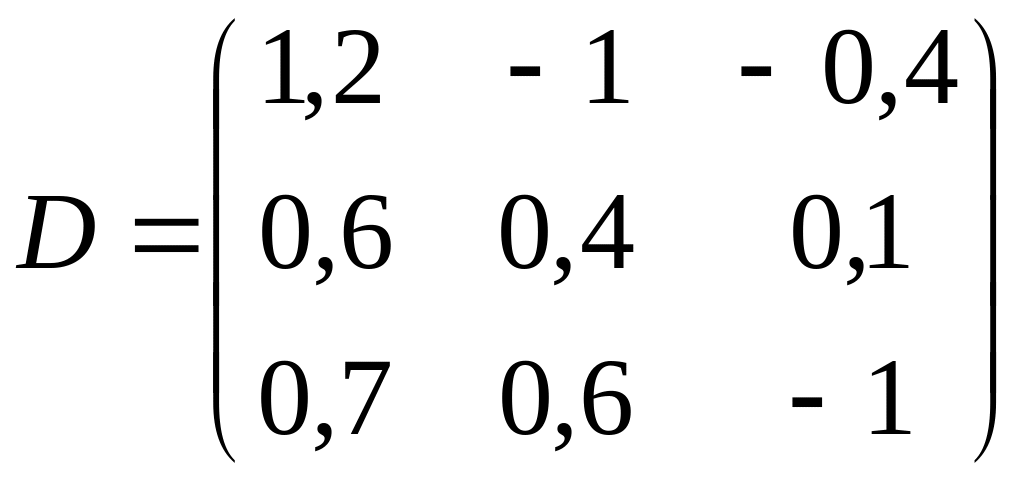 ,
;
,
;
н)
 ,
,
 ; о)
; о)
 ,
;
,
;
8. Розв‘язування нелінійних рівнянь
Mathcad
має ряд можливостей для знаходження
коренів нелінійних рівнянь. Щоб розв’язати
рівняння за допомогою функції
![]() ,
рівняння потрібно привести до вигляду,
щоб його права частина дорівнювала
нулю, вказати змінну за якою шукається
корінь та задати початкове наближення
цієї змінної.
,
рівняння потрібно привести до вигляду,
щоб його права частина дорівнювала
нулю, вказати змінну за якою шукається
корінь та задати початкове наближення
цієї змінної.
Проілюструємо
пошук коренів на прикладі рівняння
![]() .
.
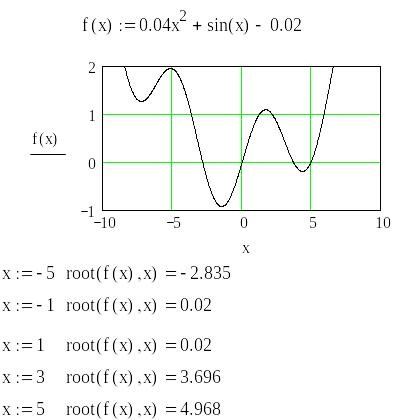
Для встановлення кількості коренів та їх початкових наближених значень будуємо графік функції . Зрозуміло, що межі зміни аргумента на графіку вибираємо декілька разів, щоб переконатися в тому, що охопили всі корені рівняння. Маючи приблизні графічні значення коренів, задаємо початкові значення для та функцію знаходження кореня рівняння. У залежності від вибору початкового значення аргумента отримуємо той чи інший корінь рівняння.
