Питання для самоперевірки та вправи

1. Які ви знаєте способи машинного представлення графа ? В яких випадках доцільно використовувати кожний спосіб ?

2. Намалюйте довільний граф, позначте його вершини і ребра. Дайте матричну інтерпретацію цього графа.

3. Дайте машинну інтерпретацію графа, створеного в пункті 2. Обгрунтуйте вибраний спосіб.

4. Створіть схему з полем зв'язків для графа, створеного в пункті 2.

Лекція №17. Операції над графами

Об’єднання, переріз, сума та різниця графів

Декартовий добуток графів

Композиція графів

Нехай і - два орієнтованих графа, множини вершин і множини ребер цих графів не перетинаються.

Об’єднанням графів називається граф , вершинами якого є множина , а відображення .

Наприклад:

:

:

Тоді об’єднанням графів буде граф:

Перерізом графів і називається граф , для якого виконуються умови , .

Наприклад:

Розглянемо переріз графів, зображених у попередніх прикладах:

Одержимо граф

Різницею графів і називається граф , для якого виконуються умови , , тобто, якщо, наприклад, множина вершин деякого графа і , то .

Різниця графів, розглянутих у попередніх прикладах буде: , . Одержимо:

Композиція графів визначається по таким правилам:

1. Вершинами результуючого графа є множина .

2. Відображення кожної вершини визначається .

Наприклад:

Створимо граф , як композицію графів :

Побудова декартового добутку визначається таким правилом:

1. Вершини графа одержуємо шляхом послідовного сполучення кожної з вершин першого графа з кожною з вершин другого графа . Отже, в графі кожна вершина має двохзначне позначення. Загальна кількість вершин графа дорівнює добутку вершин графів , так, наприклад, якщо маємо множини вершин , , тоді .

2. Відображення кожної вершини в декартовому добутку графів одержуємо шляхом можливих сполучень кожного з відображень графа з кожним з відображень графа для відповідних вершин. Загальна кількість відображень для кожної вершини графа дорівнює добутку числа відображень графів та для відповідних вершин, тобто

Наприклад:

Визначити відображення для вершини , якщо відомо ,

.

Розглянемо приклад:

Сумою графів і називається граф , який визначається по таким правилам:

1. Вершини графа визначаються аналогічно декартовому добутку .

2. Відображення для будь-якої вершини графа одержують шляхом об’єднання двох сполучень, одне з яких одержане відображенням вершини графа і вершиною графа , а друге - вершиною графа і відображенням вершини графа : .

Наприклад:

Треба визначити образ , якщо виконуються умови , . Визначимо можливі сполучення з і з .

Для прикладу визначимо суму графів які розглядались для визначення їх декартового добутку:

.

Подальшу побудову графа пропонуємо читачеві.

Операції над неорієнтованими графами

Розглянемо операції над графами і , які мають множини вершин і і множини ребер і , які не перетинаються. Тоді визначені такі операції:

Операція	Число вершин	Число ребер
Об’єднання
З’єднання +
Добуток
Композиція

Наприклад: Об’єднання:

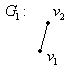
З’єднання: Добуток:

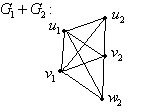
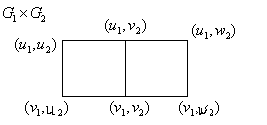
Вершини і суміжні в тоді і тільки тоді, коли і або .

Композиція:

Вершина суміжна з тоді і тільки тоді, коли або і .