
- •Лекція №14. Визначення графа як абстрактного математичного поняття
- •Питання для самоперевірки та вправи
- •Лекція №15. Матричне представлення графів
- •Питання для самоперевірки та вправи
- •Лекція №16. Машинне представлення графів
- •Питання для самоперевірки та вправи
- •Лекція №17. Операції над графами
- •Питання для самоперевірки та вправи
Питання для самоперевірки та вправи
1. Дайте означення графа, як математичного об’єкта.
2. Дайте класифікацію графів.
3. Який граф називається зв’язаним ? Якщо граф незв’язний, то яким чином можна розкласти його на компоненти ? Доведіть.
4. Що називається ступенем графа ? Яка кількість вершин непарного ступеня в графі ? Доведіть.
5.
Нехай
![]() -
кількість вершин ступеня
-
кількість вершин ступеня
![]() в графі
.
Знайти кількість попарно неізоморфних
графів
,
у яких
в графі
.
Знайти кількість попарно неізоморфних
графів
,
у яких
![]() ,
,
![]() .
.
6. Показати, що в будь-якому графі, який має не менше, ніж дві вершини, знайдуться дві вершини з однаковими ступенями.
7.
Нехай
![]() - мінімальна з ступенів вершин графа
, який має
вершин
- мінімальна з ступенів вершин графа
, який має
вершин
![]() .
Довести, що якщо
.
Довести, що якщо
![]() ,
то граф зв’язний.
,
то граф зв’язний.
Лекція №15. Матричне представлення графів
Графічне та аналітичне представлення графа
Матриця суміжності
Матриця інциденцій
Матриця ваги
Граф можна задати графічним, аналітичним або матричним способом.
Графічне представлення графа
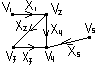
Рис. 15.1 – орієнтований граф
Аналітичне представлення графа.
![]() ,
де
-
множина вершин графа,
,
де
-
множина вершин графа,
![]() -
відображення, яке задає відповідність
між вершинами графа.
-
відображення, яке задає відповідність
між вершинами графа.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Матричне представлення графа
Матриця
суміжності графа це
матриця
![]() ,
в якій
,
в якій
![]() для орієнтованого графа. Для графа,
зображеного на малюнку 15.1 матриця
суміжності має вигляд:
для орієнтованого графа. Для графа,
зображеного на малюнку 15.1 матриця
суміжності має вигляд:
Для орієнтованого графа для співвіднесеного графа
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
0 |
|
|
0 |
0 |
1 |
1 |
0 |
|
1 |
0 |
1 |
1 |
0 |
|
|
0 |
0 |
0 |
1 |
0 |
|
0 |
1 |
0 |
1 |
0 |
|
|
0 |
0 |
0 |
0 |
0 |
|
0 |
1 |
1 |
0 |
1 |
|
|
0 |
0 |
0 |
1 |
0 |
|
0 |
0 |
0 |
1 |
0 |
Петля може бути представлена одиницею на відповідному діагональному елементі. Кратні ребра можуть бути представлені числом більшим одиниці.
Матриця
інциденції для
неорієнтованого графа з
вершинами і
![]() ребрами це матриця
ребрами це матриця ![]() ,
,
стрічки
якої відповідають вершинам, а стовпці
ребрам. Елементи матриці будуються за
правилом
![]() .
.
Матрицею
інцидентності для орієнтованого графа
з
вершинами і
ребрами називається матриця
![]() .
Елементи матриці будуються за правилом
.
Елементи матриці будуються за правилом 
Матриця інциденцій для графа, зображеного на малюнку 15.1 має вигляд:
для орієнтованого графа для співвіднесеного графа
|
|
|
|
|
|
|
+1 |
0 |
0 |
0 |
0 |
|
-1 |
+1 |
0 |
+1 |
0 |
|
0 |
-1 |
+1 |
0 |
0 |
|
0 |
0 |
-1 |
-1 |
-1 |
|
0 |
0 |
0 |
0 |
+1 |
|
|
|
|
|
|
|
1 |
0 |
0 |
0 |
0 |
|
1 |
1 |
0 |
1 |
0 |
|
0 |
1 |
1 |
0 |
0 |
|
0 |
0 |
1 |
1 |
1 |
|
0 |
0 |
0 |
0 |
1 |
Граф
називається зваженим,
якщо кожному його ребру поставлено у
відповідність число. Зважений граф може
бути представлений своєю матрицею ваги
![]() ,
де
,
де
![]() -вага ребра, яке з’єднує
вершини
-вага ребра, яке з’єднує
вершини
![]() .
Таким чином, матриця ваги графа являється
узагальненням матриці суміжності.
.
Таким чином, матриця ваги графа являється
узагальненням матриці суміжності.
Граф називається зваженим, якщо кожному його ребру поставлено у відповідність число. Зважений граф може бути представлений своєю матрицею ваги , де -вага ребра, яке з’єднує вершини . Таким чином, матриця ваги графа являється узагальненням матриці суміжності.
