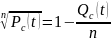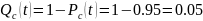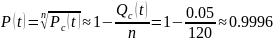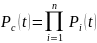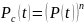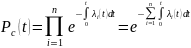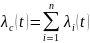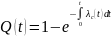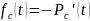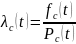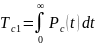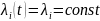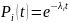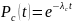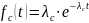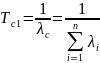- •21 Определение количественных характеристик надежности по статистическим данным об отказах изделия.
- •Теоретические сведения
- •Аналитическое определение количественных характеристик надёжности изделия.
- •Теоретические сведения
- •Последовательное соединение элементов в систему.
- •Теоретические сведения
- •Решение типовых задач.
Последовательное соединение элементов в систему.
Теоретические сведения
Соединение элементов называется последовательным, если отказ хотя бы одного элемента приводит к отказу всей системы. Система последовательно соединенных элементов работоспособна тогда, когда работоспособны все ее элементы.
Вероятность
безотказной работы системы за время
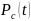 определяется
формулой:
определяется
формулой:
|
(3.1) |
Где
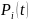 – вероятность безотказной работы -ого
элемента за время
.
– вероятность безотказной работы -ого
элемента за время
.
Если
все элементы равнонадёжны, т.е.
 ,
то
,
то
|
(3.2) |
Выразим
через интенсивность отказов
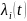 – интенсивность отказов -ого элемента.
– интенсивность отказов -ого элемента.
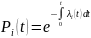
|
(3.3) |
или
|
(3.4) |
Где
 определяется соотношением:
определяется соотношением:
|
(3.5) |
Здесь – интенсивность отказов -го элемента; - интенсивность отказов системы.
Вероятность отказа
системы на интервале времени
 равна:
равна:
|
(3.6) |
Частота отказов
системы
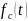 определяется соотношением:
определяется соотношением:
|
(3.7) |
Интенсивность отказов системы:
|
(3.8) |
Среднее время безотказной работы системы:
|
(3.9) |
В случае экспоненциального закона надежности всех элементов системы имеем:
|
(3.10) |
Отсюда:
|
(3.11) |
|
(3.12) |
Тогда можно определить по формуле
|
(3.13) |
Плотность находим по формуле
|
(3.14) |
Вероятность
безотказной работы
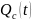 найдём по формуле:
найдём по формуле:
|
(3.15) |
Поскольку вся
система тоже будет подчиняться
экспоненциальному закону распределения
(исходя из выше написанных формул), можно
найти среднее время безотказной работы
системы
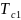
|
(3.16) |
Решение типовых задач.
Задача 3.1.
Система состоит из трех устройств.
Интенсивность отказов электронного
устройства равна
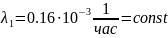 .
.
Интенсивности отказов двух электромеханических устройств зависят от времени и определяются следующими формулами:
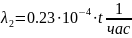
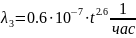
Необходимо рассчитать вероятность безотказной работы изделия в течение 100 часов.
Решение.
На основании формулы (3.3) имеем

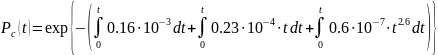
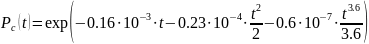
Подставим в эту формулу .
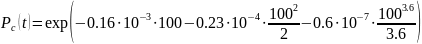
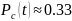
Задача 3.2.
Система состоит из трех блоков, среднее
время безотказной работы которых равно:
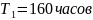 ,
,
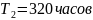 ,
,

Для блоков справедлив экспоненциальный закон надежности. Требуется определить среднее время безотказной работы системы.
Решение. Воспользовавшись формулой (3.17) получим:

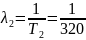
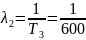
Здесь
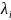 – интенсивность
отказов -го блока. На основании формулы
(3.11) имеем:
– интенсивность
отказов -го блока. На основании формулы
(3.11) имеем:

![]() Здесь
Здесь
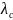 - интенсивность отказов системы.
- интенсивность отказов системы.
На основании формулы (3.16) получим:
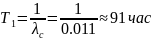
Задача 3.3.
Система состоит из 12600 элементов, средняя
интенсивность отказов которых
 .
Требуется
определить
,
,
,
для
.
Требуется
определить
,
,
,
для
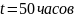 .
.
Здесь – вероятность безотказной работы системы в течение времени ;
– вероятность отказа системы в течение времени t;
– частота отказов
или плотность вероятности времени
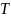 безотказной работы системы;
безотказной работы системы;
– среднее время безотказной работы системы.
Решение. Интенсивность отказов системы по формуле (3.11) будет
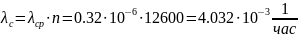
Из (3.13) имеем
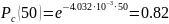
Из (3.15) получим:
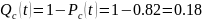
Из (3.14) имеем:
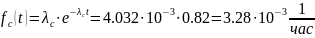
Из (3.16) получим
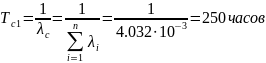
Задача 3.4. Система
состоит из двух устройств. Вероятности
безотказной работы каждого из них в
течение времени
равны:
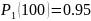 и
и
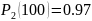 .
Справедлив
экспоненциальный закон надежности.
Необходимо найти среднее время безотказной
работы системы.
.
Справедлив
экспоненциальный закон надежности.
Необходимо найти среднее время безотказной
работы системы.
Решение. Найдем вероятность безотказной работы изделия:
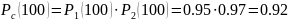
Найдем интенсивность отказов изделия, воспользовавшись формулой
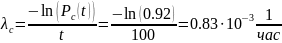
Отсюда вычислим среднее время безотказной работы:
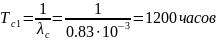
Задача 3.5.
Вероятность безотказной работы одного
элемента в течение времени
равна
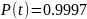 .
Требуется определить вероятность
безотказной работы системы, состоящей
из
.
Требуется определить вероятность
безотказной работы системы, состоящей
из
 таких же элементов.
таких же элементов.
Решение. Вероятность безотказной работы системы равна:

Вычислим
следующее приближённое значение при
маленьких
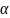 :
:
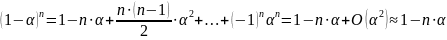
Вероятность
близка к единице, значит, мы можем её
представить в виде
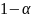 ,
где
будет мала.
Поэтому для вычисления
,
где
будет мала.
Поэтому для вычисления
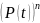 воспользуемся формулой для приближённого
вычисления значения:
воспользуемся формулой для приближённого
вычисления значения:
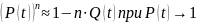
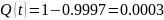
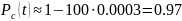
Задача.З.6.
Вероятность
безотказной работы системы в течение
времени
равна
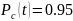 .
Система состоит из
.
Система состоит из
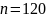 равнонадежных элементов. Необходимо
найти вероятность безотказной работы
элемента.
равнонадежных элементов. Необходимо
найти вероятность безотказной работы
элемента.
Решение.
Вероятность безотказной работы элемента будет равна:
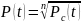
При решении прошлой задачи мы получили следующую формулу для подсчёта приближённого значения выражения для маленьких :

Обозначим
 ,
тогда
,
тогда
 .
Подставим в формулу. Получим:
.
Подставим в формулу. Получим:

Извлечём из правой и левой части корень -ой степени:

Заметим, что это как раз подходит под условие нашей задачи, ведь близка к единице, а, значит, вычисления удобно выполнить по формуле