Технология бурения скважин

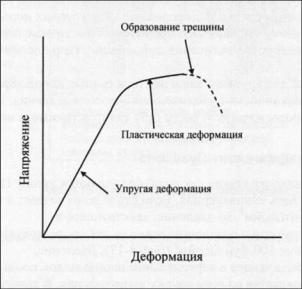
vk.com/club152685050 | vk.com/id446425943

61

Напряжение, воспринимаемое жидкостью в поровом пространстве, выражается как поровое давление. Поровое давление и эффективное напряжение вместе дают полное напряжение.

Полное напряжение = поровое давление + эффективное напряжение

Деформация и прочность образца породы зависят только от эффективного напряжения. Именно напряжение на контакте между зернами определяет

относительное перемещение этих зерен. Деформация и проскальзывание зерен относительно друг друга не зависят от порового давления. Поэтому при исследовании прочности горной породы нас интересует именно эффективное напряжение.

Увеличение порового давления приводит к уменьшению эффективного напряжения и, таким образом, к ослаблению породы.

2.3.1.3 Деформация

Деформация определяется как изменение длины или ширины образца, испытывающего напряжение. Обозначается деформация греческой буковой ε (эпсилон). Чем больше напряжение, которое испытывает порода, тем сильнее деформация.

Когда образец породы подвергается сжатию в лаборатории, он испытывает сжимающее напряжение. Путем измерений можно определить продольную и поперечную деформацию образца, испытывающего это напряжение.

.

Рис. 24 Зависимость между напряжением и деформацией образца породы при сжатии

График на рис.24 представляет собой типичную зависимость между напряжением и деформацией образца породы при сжатии. Следует отметить, что эта кривая напоминает кривую, отражающую результаты испытаний пласта на утечку. При испытании на утечку порода испытывает растягивающие напряжения, а буровой раствор - сжимающие напряжения. И порода, и буровой деформируются под действием этих напряжений.

vk.com/club152685050 | vk.com/id446425943

62

Буровой раствор находится в сжатом состоянии, а диаметр ствола увеличивается. Количество дополнительного бурового раствора, требуемого для заполнения скважины, может служить мерой суммы деформаций. Таким образом, диаграмма испытаний на утечку представляет собой график зависимости между напряжением и деформацией в координатах фунты/дюйм2 – баррели.

При низком уровне напряжений горные породы проявляют упругость. При снятии напряжения образец снова примет свои первоначальные размеры так же как резиновая лента. Прямолинейная часть графика представляет область упругих деформаций. При достижении уровня напряжений, превышающего предел упругости, произойдет необратимая деформация или разрушение образца. Такая деформация называется неупругой или пластической деформацией. Для большинства пород некоторая пластическая деформация наблюдается еще до достижения предела прочности. При превышении предела прочности образец разрушается. Мягкие глинистые породы могут испытывать большую пластическую деформацию, прежде чем будет достигнут предел прочности. Хрупкие известняки могут разрушиться сразу же после превышения предела упругости.

Хрупкость против пластичности

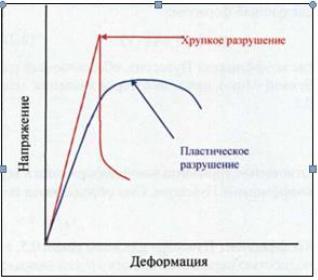
Хрупкие породы испытывают до разрушения очень небольшую пластическую деформацию. Пластичные породы испытывают до разрушения значительную пластическую деформацию (рис.25).

Рис. 25 Зависимость между напряжением и деформацией Хрупкие породы разрушаются при достижении предельного напряжения. Они достигают

в этой точке своей предельной деформации. Для хрупких пород дальнейшее увеличение нагрузки приводит к резкому уменьшению прочности. Пластичные породы могут выдерживать нагрузку даже после некоторого увеличения деформации. Разрушение пластичных пород не такое катастрофическое.

Как для хрупких, так и для пластичных пород характерно увеличение предела прочности и пластичности с увеличением бокового давления. Если боковое давление достаточно высоко, то все породы начинают вести себя как пластичные, а не как хрупкие.

vk.com/club152685050 | vk.com/id446425943

63

Коэффициент Пуассона

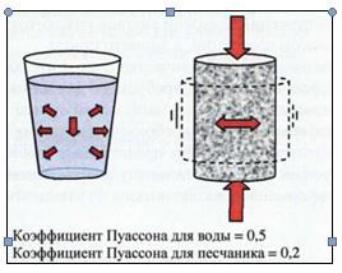
Жидкости (такие как вода) подчиняются закону Паскаля - давление передается жидкостью одинаково во всех направлениях. Если столб воды создает в высоком резервуаре гидростатическое давление 100 фунт/дюйм, то давление, действующее в горизонтальном направлении на стенку резервуара, равно 100 фунт/дюйм (рис.26). Давление, действующее в вертикальном направлении, полностью передается во всех других направлениях. В твердых телах давление, действующее в вертикальном направлении, передается в других направлениях не полностью.

Рис. 26 Коэффициент Пуассона (нагрузка, которую передает порода в горизонтальном направлении, зависит от коэффициента Пуассона, чем больше коэффициент Пуассона, тем более деформируемой является порода).

Отношение горизонтального напряжения к вертикальному напряжению выражается через коэффициент Пуассона. Оно определяется по следующей формуле:

σh / σv = ν / (1 - ν)

где коэффициент Пуассона, обозначаемый греческой буквой ν (ню), имеет некоторое значение, меньшее чем 0,5.

Отношение горизонтальной деформации к вертикальной деформации также выражается через коэффициент Пуассона. Оно определяется по формуле:

εh / εv = ν

Коэффициент Пуассона для воды равен 0,5, т.е. давление, действующее в вертикальном направлении, полностью передается во всех других направлениях. Коэффициент Пуассона для горной породы можно определить, подсчитав отношение поперечной деформации к продольной деформации.

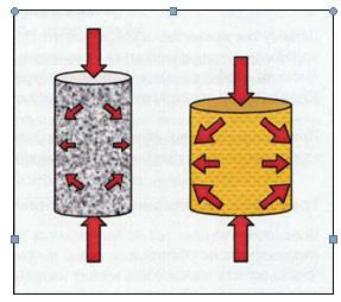
Для мягких, молодых глинистых пород характерны высокие значения коэффициента Пуассона, поэтому горизонтальные напряжения в естественных условиях залегания высоки. Крепкие и хрупкие породы (такие как древние доломиты) имеют меньший коэффициент Пуассона, поэтому в них меньшая часть вертикальной нагрузки передается в горизонтальном направлении (рис.27).

vk.com/club152685050 | vk.com/id446425943

64

Рис. 27 Поведение под нагрузкой хрупких и пластичных пород

Иначе говоря, некоторые породы деформируемы в большей степени чем другие; и они имеют относительно больший коэффициент Пуассона. Более хрупкие породы имеют меньший коэффициент Пуассона; они меньше деформируются под нагрузкой.

Коэффициент Пуассона для твердых песчаников может составлять всего лишь 0,01. Для известняков этот показатель изменяется от 0,15 до 0.31.

Значения коэффициента Пуассона для глинистых пород изменяются от 0,17 до 0.28, а для глины могут быть как низкими - 0,17, так и высокими - 0,50 (для очень влажных глин).

Почему так важно знать коэффициент Пуассона для разбуриваемой породы? Потому что пластичные породы могут выдавливаться в скважину под весом вышележащих пород. Для проходки пород с высоким коэффициентом Пуассона потребуется более плотный буровой раствор, поскольку в этом случае нужно предотвратить выдавливание или обрушение породы в скважину.

При определении коэффициента Пуассона в лаборатории принимается, что боковое давление одинаково со всех сторон. Однако в земной коре это не так.

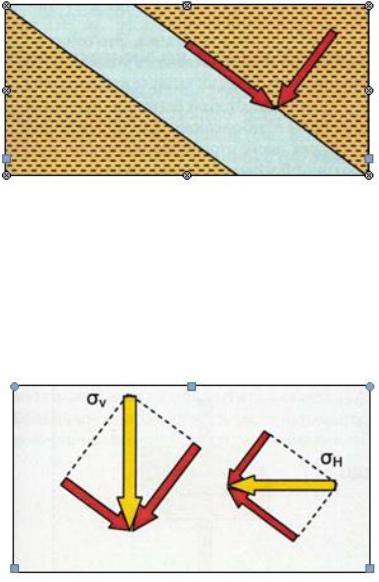
Трехосное напряженное состояние и главные напряжения

Поведение твердых тел не подчиняется закону Паскаля. Напряжение, действующее в одном направлении, не обязательно равно напряжению, действующему в перпендикулярном направлении. Чтобы понять зависимость между напряжением и деформацией для твердых тел, нужно представить себе трехосное (объемное) напряженное состояние. Трехосное напряженное состояние элемента характеризуется тремя главными напряжениями (рис.28).

Термин главные напряжения означает, что одно из этих напряжений является максимальным напряжением, воспринимаемым элементом, а другое - минимальным. Третье (промежуточное) главное напряжение является ортогональным по отношению к максимальному и минимальному напряжениям.

vk.com/club152685050 | vk.com/id446425943

66

Компоненты напряжений

Главные напряжения в земной коре действуют в вертикальном и горизонтальном направлениях. Скважины не всегда являются строго вертикальными или горизонтальными. Больше всего нас интересуют напряжения, действующие параллельно или перпендикулярно траектории скважины (рис.30). Чтобы найти эти напряжения, нужно рассмотреть компоненты напряжений.

Рис.30 Напряжения на стенках скажины (напряжения на стенках скважины действуют параллельно и перпендикулярно траектории скважины).

Компонента напряжений - это та часть напряжений, которая действует в интересующем нас направлении (рис.31). Любое напряжение, действующее под некоторым углом к траектории нашей скважины, можно разложить на две компоненты напряжений, одна из которых направлена вдоль траектории, а другая - перпендикулярно к ней. Величину напряжений можно найти с использованием простых тригонометрических формул.

Рис.31 Компоненты напряжений на стенках скважины (напряжения на стенках скважины можно найти суммированием компонент вертикальных и горизонтальных напряжений).

Напряжения в естественных условиях залегания

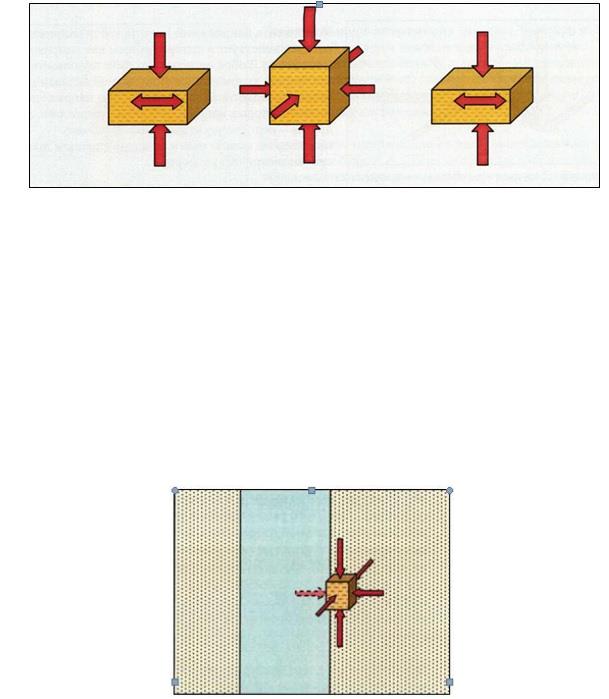
Рассмотрим элементарный кубик породы в естественных условиях залегания. Это означает отсутствие возмущений в пласте (рис.32). Когда порода находится в естественных условиях залегания, элементарный кубик находится в равновесном состоянии. Массив вышележащих пород давит на кубик, как гидравлический пресс в лаборатории. Напряжение от этой нагрузки стремится сделать элементарный кубик короче

vk.com/club152685050 | vk.com/id446425943

68

Напряжение, действовавшее в удаленном материале, должно быть восполнено давлением бурового раствора в скважине и напряжением, действующим со стороны других кубиков, оставшихся на стенке. Если в скважине нет жидкости, то 100 % напряжений передается на стенку как кольцевое напряжение. Кольцевое напряжение является тангенциальным по отношению к стенке скважины. Кольцевое напряжение σ θ часто называют тангенциальным или окружным напряжением.

Кольцевые напряжения

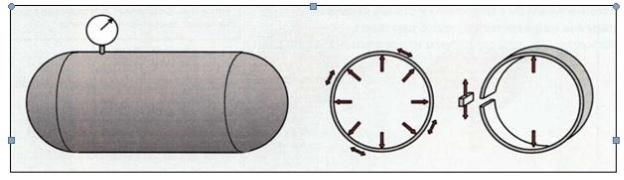
Мы будет так много говорить о кольцевых напряжениях, что имеет смысл объяснить это понятие подробнее. Для этого рассмотрим сосуд давления, показанный на рис.34. Если разделить сосуд пополам вертикальной плоскостью, то обе половины будут стремиться разойтись. Внутреннее давление, действующее на поперечное сечение каждой половины сосуда, создаст усилие, раздвигающее эти половины. Сила, удерживающая вместе обе половины, обусловлена растягивающим напряжением в стенках сосуда. По величине эта сила равна произведению напряжения на площадь поперечного сечения стенки. Численно она равна силе, стремящейся раздвинуть обе половины. Это кольцевое напряжение остается неизменным по всему периметру сосуда, если не изменяется толщина стенки.

Рис.34 Кольцевые напряжения (Внутреннее давление стремится раздвинуть половины сосуда. В результате в стенках сосуда возникает растягивающее кольцевое напряжение. Если погрузить этот сосуд глубоко в море, в стенках будут действовать сжимающие кольцевые напряжения).

Представим себе, что тот же самый сосуд испытывает давление извне, как при погружении глубоко в море. Теперь наружное давление, действующее на ту же площадь, удерживает обе половины сосуда вместе. Кольцевые напряжения в любом месте сосуда являются сжимающими.

А сейчас посмотрим на сосуд, показанный на рис.35. Когда по оси y действует сила 10 тыс. фунтов, кольцевые напряжения в плоскости x-z равны 1 тыс. фунт/дюйм. Когда по оси x действует сила 5 тыс. фунтов, кольцевые напряжения в плоскости y-z равны 500 фунт/дюйм2. Две не равные по величине силы создают кольцевые напряжения разной величины.

vk.com/club152685050 | vk.com/id446425943

69

Рис. 35 Кольцевые напряжения

Теперь давайте вернемся к нашему элементарному кубику породы, находящемуся в естественных условиях залегания. Если ствол скважины проходит рядом с этим кубиком, и с одной стороны удалена порода, создающая боковое давление, то недостающие напряжения восполняются кольцевыми напряжениями. Можно посмотреть на эту ситуацию и таким образом, что теперь поле напряжений должно обойти вокруг скважины

(рис.36).

Рис.36 Распределениеинапряжений вокруг ствола скважины (Поскольку в процессе бурения удаляется порода, происходит перераспределение напряжений и возникают кольцевые напряжения).

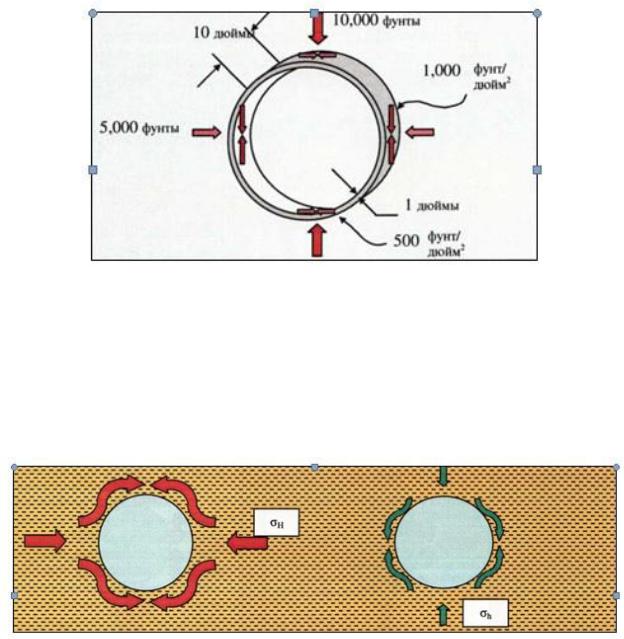
Если скважина вертикальная, и нет тектонических напряжений, то горизонтальные напряжения (σH и σh) равны, и кольцевые напряжения равномерно распределены вокруг ствола скважины (рис. 37А).

Поскольку тектонические напряжения в той или иной степени существуют везде, то при любом распределении напряжений горизонтальные напряжения будут больше в одном направлении, чем в остальных. Наибольшие горизонтальные напряжения σH должны обойти скважину, как кольцевые напряжения. Это же относится и к наименьшим горизонтальным напряжениям σh. В результате возникают кольцевые напряжения, которые имеют максимальное значение на направлениях, отстоящих на 90° и 270° от направления действия наибольших главных горизонтальных напряжений (рис. 37В).

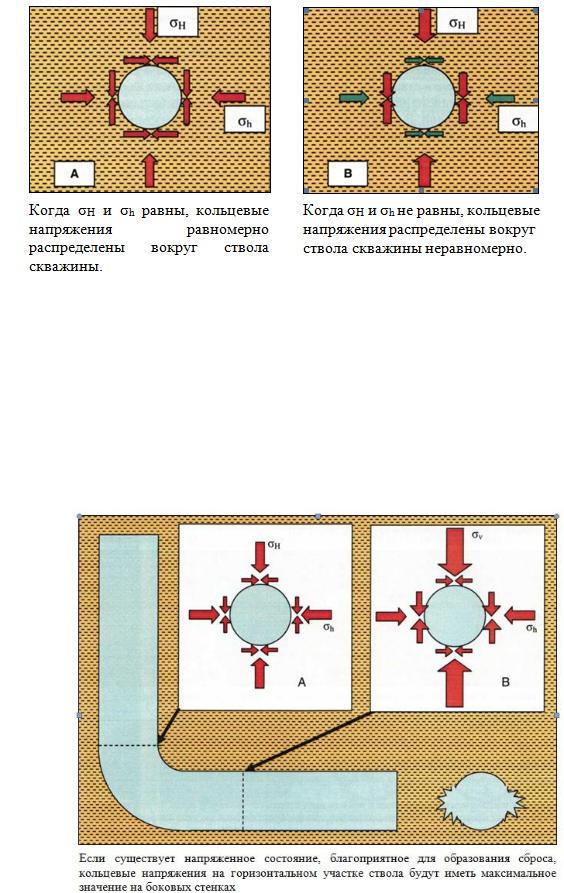
vk.com/club152685050 | vk.com/id446425943

70

Рис. 37 Кольцевые напряжения на стенках скважины

Посмотрим на скважину, изображенную на рис.38. Принимаем, что тектонические напряжения равны (о"н = 0"ь), тогда кольцевые напряжения на стенках скважины будут распределены равномерно по всей окружности сечения ствола, как показано на рис. 37А. Однако на горизонтальном участке ствола вертикальные напряжения от веса вышележащих пород будут больше действующих горизонтальных напряжений. В результате кольцевые напряжения будут иметь максимальное значение на боковых стенках, и наименьшие значения на верхней и нижней стенках (рис. 37В). Если плотность бурового раствора недостаточно велика, стенки обрушатся в скважину.

Рис. 38 Анизатропное распределение напряжений