Задача 1. Выведение ла на орбиту спутника Луны за заданное время

Рассмотреть управляемый процесс выведения одноступенчатого ЛА с поверхности Луны на круговую орбиту спутника при нерегулируемой по величине тяге двигательной установки. Управление осуществляется только изменением направления вектора тяги Р.

При построении математической модели учесть следующие допущения :

1) ЛА рассматриваем как материальную точку переменной массы m(t);

2) Луна сферическая и не вращается;

3) орбита спутника круговая;

4) на ЛА действуют сила тяжести G=μm/r² и сила тяги P=const;

5) поле тяготения центральное;

6) траектория движения ЛА плоская.

Тогда основные закономерности, описывающие связи между характеристиками рассматриваемого процесса, представляются уравнениями движения ЛА в проекциях на радиус-вектор центра масс ЛА и направление, перпендикулярное ему, в виде:

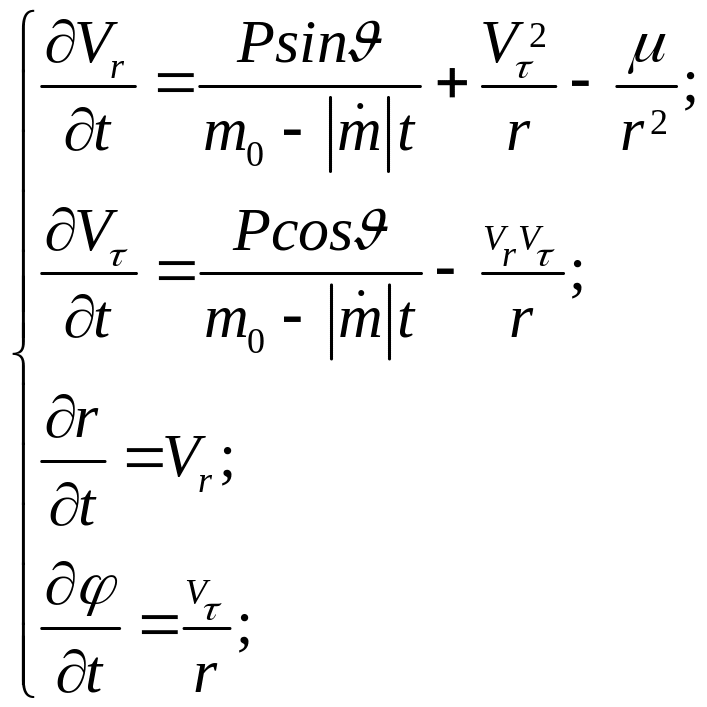
где μ – гравитационный параметр Луны; r – радиальное расстояние ЛА от центра Луны; – радиальная компонента скорости; – тангенциальная компонента скорости; m₀ – начальная масса ЛА; – секундный расход массы;  – угол между вектором тяги и местным горизонтом; φ – полярный угол между текущим и начальным радиус-векторами; μ, m₀, ,P – заданные числа.

Рассчитать траекторию выведения ЛА на круговую орбиту заданного радиуса c орбитальной скоростью 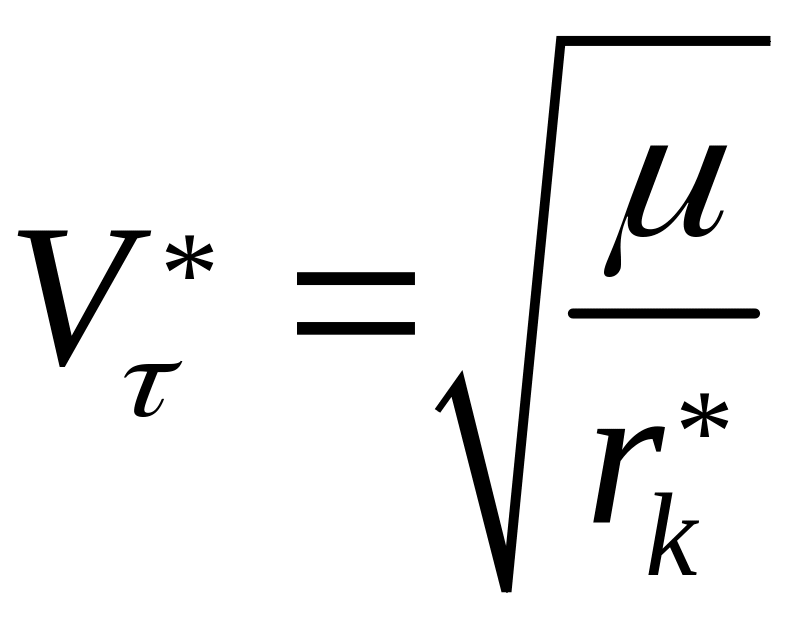за заданное время t_k-t₀.

Задача 2. Выведение ла на заданную орбиту спутника Луны

Рассмотреть управляемый процесс выведения одноступенчатого ЛА с поверхности Луны на круговую орбиту спутника при нерегулируемой по величине тяге двигательной установки. Управление осуществляется только изменением направления вектора тяги Р.

При построении математической модели учесть следующие допущения :

1) Ла рассматриваем как материальную точку переменной массы m(t);

2) Луна сферическая и не вращается;

3) орбита спутника круговая;

4) на ЛА действуют сила тяжести G=μm/r² и сила тяги P=const;

5) Поле тяготения центральное;

6) траектория движения ЛА плоская.

Тогда основные закономерности, описывающие связи между характеристиками рассматриваемого процесса, представляются уравнениями движения ЛА в проекциях на радиус-вектор центра масс ЛА и направление, перпендикулярное ему, в виде:

где μ – гравитационный параметр Луны; r – радиальное расстояние ЛА от центра Луны; – радиальная компонента скорости; – тангенциальная компонента скорости; m₀ – начальная масса ЛА; – секундный расход массы;  – угол между вектором тяги и местным горизонтом; φ – полярный угол между текущим и начальным радиус-векторами; μ, m₀, ,P – заданные числа.

Рассчитать траекторию, обеспечивающую выведение ла с поверхности Луны на заданную круговую орбиту радиуса с орбитальной скоростью . Задача 3. Мягкая стыковка ла на орбите

Рассмотреть управляемый процесс сближения двух ЛА на орбите. ЛА, выполняющий пассивную роль и не производящий манёвров с целью сближения, находится на заданной монтажной орбите. Управление движением активного ЛА осуществляется путём изменения величины и направления тяги его двигательной установки.

Составить математическую модель процесса сближения, предполагая, что : 1) монтажная орбита круговая; 2) активный ЛА находится в плоскости монтажной орбиты; 3) на активный ЛА действуют сила тяжести и сила тяги двигательной установки; 4) поле тяготения центральное.

Закономерности, связывающие характеристики процесса сближения, наиболее просто записываются в виде дифференциальных уравнений относительного движения в декартовой системе координат, начало которой совпадает с центром масс пассивного ЛА, ось y направлена по радиусу-вектору, проходящему из центра притяжения через начало координат, ось x ей перпендикулярна :

,

где  – гравитационный параметр притягивающего тела; r – расстояние от пассивного ЛА до центра этого тела; a_x и a_y – проекции управляющего ускорения на оси x и y.

Предполагая, что на активном ЛА стоят раздельные двигатели с регулируемой величиной тяги параллельно каждой из осей x и y, считать управляющими воздействиями независимые функции времени a_x=a_x(t) и a_y=a_y(t).

Найти траекторию, обеспечивающую сближение рассматриваемых ЛА за заданное время t_k-t₀ с некоторой исходной позиции до состояния мягкой стыковки, когда x(t_k)=0, (t_k)=0, y(t_k)=0, (t_k)=0 .