3.4.Критерий минимаксного риска Сэвиджа

При использовании вышеперечисленных критериев возмож­ны ситуации, когда неконтролируемые факторы будут действо­вать более благоприятным образом по сравнению с наихудшим состоянием, на которое ориентировалось ЛПР. Например погод­ные условия оказываются более благоприятными по сравнению с прогнозируемыми. Количество конкурентов на тех или иных рынках оказывается существенно меньше по сравнению с теми ожиданиями, на которые ориентировались производители.

В подобных ситуациях полезный результат может значитель­но отличаться от того, который обеспечивается при реализа­ции критерия гарантированного результата или критерия песси­мизма.

Поэтому возникает необходимость определения возможных отклонений полученных результатов от их оптимальных значе­ний. Здесь находит применение критерий Сэвиджа. Выбор стра­тегии аналогичен выбору стратегии по принципу Вальда с тем отличием, что игрок руководствуется не матрицей выигрышей Е, а матрицей рисков R, построенной по формуле (5.2.2).

Критерий Сэвиджа формулируется следующим образом:

(5.3.7.)

Пример 5.6. Матрица полезного результата имеет вид, пред­ставленный в табл. 5.4. Найдем значения

а за тем по формуле (5.2.2) строим матрицу рисков (табл.5.5).

Таблица 5.5 – Анализ коммерческого риска при неопределенной конъюктуре

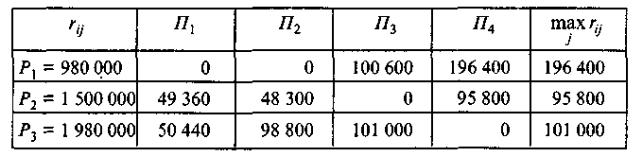В данном случае Е_тс = min {196 400, 95 800, 101 000} = 95800. Следовательно, выбирается стратегия Р₂, при которой величина риска, равная 95 800 д.е., принимает минимальное значение в са­мой неблагоприятной ситуации.

Сущность этого критерия в стремлении избежать большого риска при выборе решения. В соответствии с этим критерием (см. табл. 5.4) следует производить продукцию в объеме Р₂ = 1 500 000 д.е.

Таким образом, критерий Сэвиджа минимизирует возможные потери. Основным исходным допущением этого критерия являет­ся предположение о том, что на выбор вариантов обстановки ока­зывают влияние действия разумных противников (природы), ин­тересы которых прямо противоположны интересам ЛПР. Поэто­му, если у противников (конкурентов) имеется возможность извлечь какие-либо преимущества, то они это обязательно сдела­ют. Это обстоятельство заставляет ЛПР обеспечить минимизацию потерь вследствие этих действий.

3.5. Критерий обобщенного макснмина (пессимизма-оптимизма) Гурвица

Критерий Гурвица позволяет учитывать комбинации наихуд­ших состояний. Этот критерий при выборе решения рекомендует руководствоваться некоторым средним результатом, характери­зующим состояние между крайним пессимизмом и безудержным оптимизмом.

В соответствии с этим компромиссным критерием для каждо­го решения определяется линейная комбинация минимального и максимального выигрышей.

и предпочтение отдается варианту решения, для которого ока­жется максимальным показатель Е_i т.е.

где к — коэффициент, рассматриваемый как показатель оптимизма

При к = 0 критерий Гурвица совпадает с максимаксным критерием, т.е. ориентация на предельный риск, так как боль­ший выигрыш сопряжен, как правило, с большим риском. При к=1 — ориентация на осторожное поведение. Значения к меж­ду 0 и 1 являются промежуточными между риском и осторожно­стью и выбираются в зависимости от конкретной обстановки и склонности к риску ЛПР.

Пример 5.7. Анализируется матрица полезного результата, имеющая вид табл. 5.4. При значении коэффициента оптимизма к = 0,6 найдем оптимальную стратегию Pi.

Вычисляем для каждой стратегии линейную комбинацию;

Выбираем наибольшее из этих значений:

Еiz - шах{108460; 119084; 147756}.

В соответствии с критерием Гурвица средний размер прибыли будет равен 147 756 у.е. при выборе объема производства Р₃ = 1 980 000 у.е.

Применительно к матрице рисков R критерий Гурвица имеет вид:

(5.3.9)

Пример 5.8. Рассматривается матрица коммерческого риска, приведенная в табл. 5.5. Необходимо определить оптимальную стратегию с помощью критерия Гурвица (5.3.9).

Вычисляем при коэффициенте оптимизма к = 0,6 линейные комбинации:

Находим , что отвечает вы­бору объема производства Р₂ = 1500000 у.е.

Пример 5.9. Анализируется матрица выпуска новых видов про­дукции, приведенная в табл. 5.2. Исследовать зависимость Е_i от различных значений коэффициента оптимизма k и показать оп­тимальные решения.

Результаты вычислений по формуле (5.3.8) сведены в табл. 5.6.

Таблица 5.6 - Значения показателей и для различных к

Как видим, с изменением коэффициента k изменяется вариант решения, которому следует отдать предпочтение.

Сведем все критерии оптимальности в табл. 5.7.

Таблица 5 .7 Таблица коэффициентов оптимальности