3. Критерии эффективности в условиях полной неопределенности

Неопределенность, связанную с отсутствием информации о вероятностях состояний среды (природы), называют «безнадеж­ной» или «дурной».

В таких случаях для определения наилучших решений исполь­зуются следующие критерии:

критерий гарантированного результата (максиминный кри­терий Вальда) — это пессимистический по своей сути критерий, потому что принимается во внимание только самый плохой из всех возможных результатов каждой альтернативы. Этот подход ус­танавливает гарантированный минимум, хотя фактический ре­зультат может и не быть настолько плохим;

критерий оптимизма (критерий максимакса) соответствует оп­тимистической наступательной стратегии; здесь не принимается во внимание никакой возможный результат, кроме самого лучшего;

критерий пессимизма характеризуется выбором худшей аль­тернативы с худшим из всех худших значений окупаемости;

критерий минимаксного риска Сэвиджа можно рассматри­вать как критерий наименьшего вреда, который определяет худ­шие возможные последствия для каждой альтернативы и выбира­ет альтернативу с лучшим из плохих значений;

критерий обобщенного максимина (пессимизма — оптимиз­ма) Гурвица позволяет учитывать состояние между крайним пес­симизмом и безудержным оптимизмом. В определенных обстоя­тельствах каждый из этих методов имеет свои достоинства и не­достатки, которые могут помочь в выработке решения.

При сравнительном анализе критериев эффективности неце­лесообразно останавливаться на выборе единственного критерия, так как в ряде случаев это может привести к неоправданным ре­шениям, ведущим к значительным потерям экономического, со­циального и иного содержания. Поэтому в указанных ситуациях имеется необходимость применения нескольких критериев в со­вокупности. Например, наряду с критерием гарантированного результата может быть использован критерий Сэвиджа, критерий оптимального поведения может дополняться применением песси­мистического критерия и т.д.

Применение различных критериев эффективности для различ­ных задач выбора оптимальных решений в условиях неопределен­ности показывает, что подход, базирующийся на комплексном применении указанных критериев, может стать определяющим.

3.1. Критерий гарантированного результата

Его также называют максиминным критерием Вальда. Сущность данного критерия заключается в следующем. ЛПР располагает мно­жеством стратегий (вариантов, альтернатив) решения проблемы:

Указанные стратегии считаются контролируемыми (управля­емыми) факторами. Наряду с факторами управляемыми действу­ют факторы, которые не поддаются контролю. Обозначим их

через

В качестве P_i могут быть: технические параметры проектиру­емых систем, экономические показатели состояния предприятия, различные варианты решения поставленных задач и т.п.

Факторы П_j представляют: уровень спроса на товары, предла­гаемые фирмой, рыночные цены, условия эксплуатации техничес­ких и производственных систем, действия конкурентов и т.д.

Для оценки эффективности принимаемых решений вводим показатель эффективности Е и считаем, что функция Е(Р, П) яв­ляется известной. Так как факторы Р и П являются дискретными, то и эффективность Е также представляет собой множество диск­ретных чисел. Таким образом, каждой точке контролируемых и неконтролируемых факторов (P_i П_j), ставится в соответствие зна­чение эффективности Е (P_i П_j). Следовательно, можно построить

матрицу которая представлена в виде табл. 5.1.

Для каждого контролируемого фактора Р_i (строки) находится , в результате чего определяется набор значений по­казателя эффективности . Сравнивая полученные величины, выбирают управляемый фак­тор при котором обеспечивается максимальное значе­ние Е(Р, П).

Таблица 5.1- Матрица эффективности

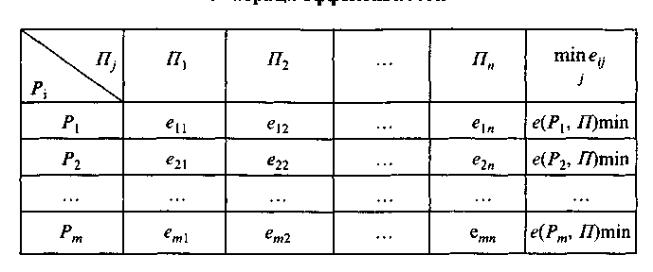
Таким образом, критерий гарантированного результата (максиминный критерий Вальда) записывается в виде

:

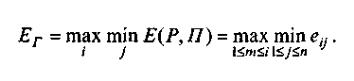Данный критерий обеспечивает максимизацию минимально­го выигрыша или, что то же самое, минимизацию максималь­ных потерь, которые могут быть при реализации одной из стра­тегий. Критерий прост и четок, но консервативен в том смысле, что ориентирует принимающего решение на слишком осторож­ную линию поведения. Величина, соответствующая максималь­ному критерию, называется нижней ценой игры, под которой следует понимать максимальный выигрыш, гарантируемый в игре с данным противником выбором одной из своих стратегий при минимальных результатах. Это перестраховочная позиция край­него пессимизма, рассчитанная на худший случай. Такая страте­гия приемлема, например, когда игрок не столь заинтересован в крупной удаче, но хочет себя застраховать от неожиданных проигрышей. Выбор такой стратегии определяется отношением игрока к риску.

Рассмотрим следующую задачу. Пусть, например, предприя­тие готовится к переходу на новые виды продукции, при этом воз­можны четыре решения P₁, Р₂, Р₃, Р₄, каждому из которых соот­ветствует определенный вид выпуска или их сочетание.

Результаты принятия решений существенно зависят от обста­новки, которая в значительной мере неопределенна. Варианты обстановки характеризует структура спроса на новую продукцию, которая может быть трех типов: П₁, П₂, П₃.

Выигрыш, характеризующий относительную величину ре­зультата (доходы, прибыль и т.п.), соответствующий каждой паре сочетаний решений Р и обстановки П, представлен в табл. 5.2.

Таблица 5.2 - Эффективность выпуска новых видов продукции

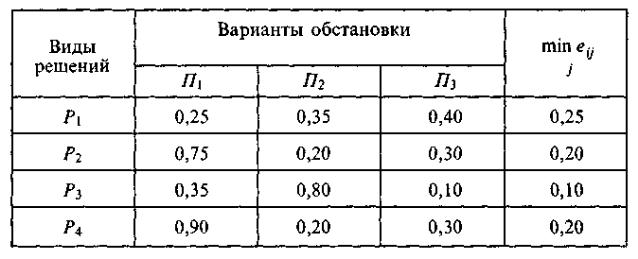
Нужно найти такую стратегию (линию поведения) Pi которая по сравнению с другими является наиболее выгодной (оптимальной). Показатель эффективности

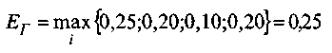
и, следовательно, предпочтение необходимо отдать вариан­ту Р₁

Выбрав решение Р₁, мы независимо от вариантов обстановки получим выигрыш не менее 0,25. При любом другом решении, в случае неблагоприятной обстановки, может быть получен резуль­тат (выигрыш) меньше 0,25. Так, при выборе решений Р2, полу­ченный выигрыш, в зависимости от наступившего варианта об­становки, будет колебаться от 0,2 до 0,75. Для решений P₃ и Р₄ границы, в которых будет колебаться выигрыш, составят 0,10 - 0,80 и 0,20 - 0,90.

Отметим еще раз, что этот критерий ориентирует ЛПР на слишком осторожную линию поведения. Так этот критерий ни­как не учитывает, что в случае принятия решения (т.е. при ори­ентации на выигрыш 0,25), максимальный выигрыш не превыша­ет 0,4. В то время, как выбирая, например, решение Р3, при гаран­тированном выигрыше 0,1 в случае благоприятной обстановки можно получить выигрыш равный 0,80.

В ряде экономических задач в качестве критерия эффективно­сти принимаемых решений выступает показатель минимума зат­рат. В этих ситуациях принцип гарантированных затрат форму­лируется в виде

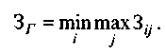(5.3.2)

В качестве затрат могут выступать: капитальные вло­жения, валовые издержки производства, приведенные годовые затраты и другие показатели.

Пример 5.1. Производится сравнение различных инвестици­онных проектов Пр1, Пр₂, ... , Пр_m. Для реализации каждого из проектов необходима определенная величина капитальных вло­жений K = {Кi}, i = . величины Ki являются управляющими (контролируемыми) факторами.

Каждому проекту соответствует определенное значение себес­тоимости продукции, которую предполагается выпускать при ре­ализации проекта. Совокупность значений себестоимости продук­ции представляется в виде:

Величины C_j на начальных этапах выполнения проекта точно определить невозможно, поэтому они считаются неконтролируе­мыми факторами. Каждой паре К_i ,С_j соответствует опреде­ленное значение приведенных годовых затрат, определяемых по формуле

где — нормативный коэффициент эффективности капитальных вложе­ний.

Располагая наборами , составляем матрицу приве­денных затрат , которая приведена в табл. 5.3.

Таблица 5.3 - Зависимость приведенных затрат от K и С

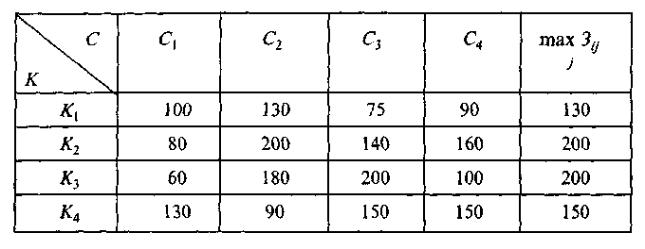
Критерий гарантированных затрат реализуется как с-

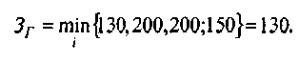
В качестве наиболее эффективной выступает первая стратегия, которой соответствуют капитальные вложения К₁