2.2.Операции с процентами

Если ставка простая, то начисляемые проценты на депозит или по кредиту рассчитываются как произведение процентной став­ки r на количество лет и (или их соответствующих долей) до сро­ка погашения и суммы вклада Р.

Так, если разместить 1000 у.е. на 9 месяцев под 8% годовых, то проценты начисленные по простой ставке, будут равны:

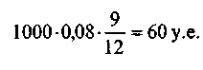
будущая стоимость депозита составит:

Тогда в общем виде формула для нахождения будущей сто­имости по простой процентной ставке выглядит так:

Наращение по сложным процентам относится к периодичес­кому добавлению накопленных процентов к основной сумме дол­га, то есть накопленные проценты добавляются к основной сумме и полученная увеличенная сумма является исходной для начисле­ния процентов в следующем периоде. При фиксированной про­центной ставке инвестирование на один период, соответствующий процентной ставке по сложным и простым процентам, приводит к одному и тому же наращенному значению. Поэтому начисление сложных процентов эквивалентно начислению простых процен­тов при реинвестировании средств в конце каждого периода. Следовательно, будет справедливой следующая формула, называемая формулой сложных процентов:

Р₁ = Р( 1 + i)^t (4.2.2)

где Р₁ — наращенная за время сумма

t - срок в периодах, соответствующий

процентной ставке i;

i — коэффициент дисконтирования (процентная ставка в долях);

Р — основной капитал (текущая стоимость вклада).

Графики зависимости наращенного значения капитала от срока t для фиксированных процентных ставок приведены на рис. 4.4 (Р = 1).

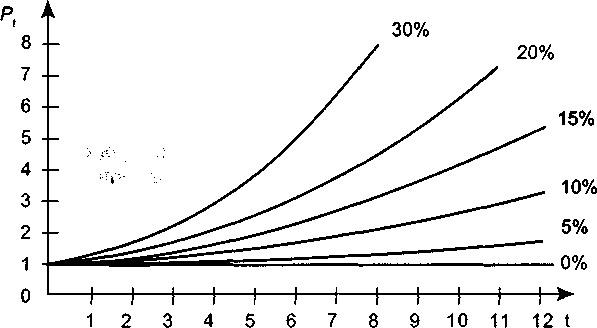
Рис. 4.4

Для получения формулы наращения, когда проценты начис­ляются чаще, чем раз в год, необходимо изменить выражение (4.2.2.). Годовая процентная ставка делится на количество перио­дов начисления в году, а степень t умножается на количество пе­риодов начисления в году:

Р₁ = Р( 1 + i/m)^t*m

где m — количество периодов начисления в году.

До сих пор мы рассматривали случаи дискретного начисле­ния процентов. Представляет интерес определить процент как результат непрерывного начисления.

В начальный момент времени имеется вклад Р. Поставим за­дачу добиться к концу года максимального роста этой суммы. Если банк дает i% годовых, то за год хранения вклад возрастет на i%, за любой меньший срок вклад возрастет пропорционально этому сроку, например, за один месяц прирост составит i/12%, а за один день i/365%. Если представить себе (только теоретически), что опе­рация открытия — закрытия вклада производится непрерывно, то можно рассмотреть следующую общую задачу.

Сумма Р, вложенная в банк под i% годовых, хранится t лет. Разделив отрезок [0; t] на n равных периодов, получим теорети­чески возможную конечную сумму:

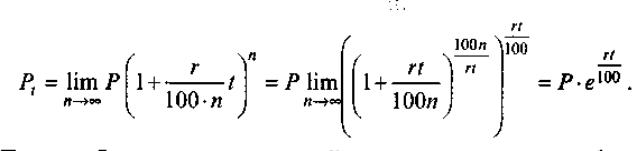
Таким образом, для конечной суммы вклада имеем формулу непрерывных процентов:

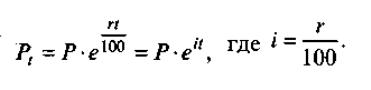(4.2.4)

Например, при годовой ставке i = 100% можно к концу второ­го года получить Р = Ре² =Р • 7,41, т.е. увеличить начальный вклад более чем в семь раз.

Пример 4.1. Найти разницу наращенных за два года значений на сумму 300 тыс. у.е. по ставке 10% при непрерывном и ежеме­сячном начислении процентов.

При непрерывном начислении процентов наращенная сумма будет:

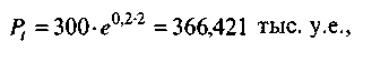
а при ежемесячном начислении процентов наращенная сумма равна:

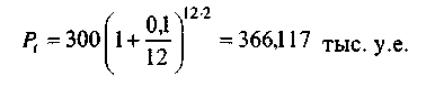
и разница составляет:

366421 -366117 = 304 у.е.