5.4. Платежи по кредитам

Многообразие форм кредитования и инвестирования обуслов­ливает необходимость нахождения критерия наиболее выгодного помещения капитала. Поясним: нам встречается два рекламных объявления; один банк предлагает 15,5% ежеквартально, а дру­гой — 15,2% ежемесячно. Что лучше? Для того чтобы ответить на этот и подобные вопросы, вводится вспомогательное понятие — эффективная процентная ставка.

Если на основной вклад Р в течение года m раз начисляются сложные проценты, то при годовой процентной ставке г ожидае­мый вклад Р, через год составит:

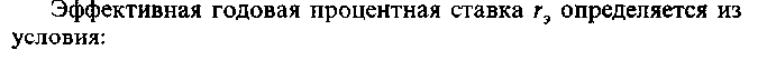
Приравнивая правые части уравнений,

/

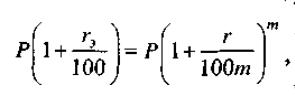
окончательно находим

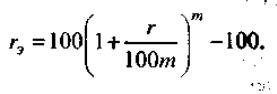
В отличие от эффективной ставки rэ первоначальная ставка r с m-кратным начислением называется номинальной. Теперь мы го­товы ответить на вопрос, какое предложение выгоднее: 15,5% ежек­вартально или 15,2% ежемесячно.

В первом случае

Отсюда", используя полученную формулу (4.5.3), находим

r_э = 16,4244%.

Во втором случае

По той же формуле

r_э = 16,3049%.

Таким образом, 15,5% ежеквартально дает больший годовой доход, чем 15,2% ежемесячно.

Полученная формула (4.4.5) имеет еще одно полезное приме­нение: расчет платежей погашения по заданной величине креди­та. Самый простой пример — взятие ссуды в банке для покупки какой-либо вещи с последующим погашением долга периодичес­кими равными платежами. Положим, вы берете в банке 5000 для приобретения автомобиля. У банка должен быть свой «интерес», поэтому его условия таковы: срок погашения кредита 3 года, про­центная ставка — 12% годовых ежемесячно. Напомним, что фраза «12% годовых ежемесячно» означает сложные ежемесячные проценты в размере = 1 %.

Спрашивается, каковы должны быть ваши ежемесячные пла­тежи, если по условию они одинаковы по величине. Для решения этой и подобных задач удобно формулу (4.4.5) представить в виде:

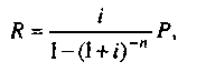
где Р — величина кредита,

r = i *100 — процентная ставка:

R — искомый размер платежа;

n — общее число платежей.

Применим полученную формулу для решения примера о по­купке автомобиля. Подставляя численные значения

легко находим размер платежа

R = 166,07.

Следует заметить, что общая сумма ваших платежей составит:

36 * 166,07 = 5978,52,

т.е. превышает (и существенно) стоимость автомобиля, равную 5000. Это превышение и есть «интерес» банка.

Если по условиям займа должник обязуется вернуть сумму долга в конце срока в виде разового платежа, то он должен пред­принять меры для обеспечения этого. При значительной сумме долга обычная мера заключается в создании погасительного фон­да, который создается из последовательных взносов должника (например, на специальный счет в банке), на которые начисляют­ся проценты. Таким образом, должник имеет возможность после­довательно инвестировать средства для погашения долга. Очевид­но, что сумма взносов в фонд вместе с начисленными процента­ми, накопленная в погасительном фонде к концу срока долга, должна быть равна его сумме. Взносы могут быть как постоян­ными так и переменными во времени. Задача заключается в опре­делении размеров срочных уплат и составляющих их элементов в зависимости от конкретных условий займа.

Пример 4.26. Кредит в сумме 100000 у.е. выдан на пять лет по ставке 12% годовых. Проценты на кредит должны выплачиваться в конце каждого полугодия. Найти необходимую величину выплат в фонд погашения долга, если проценты на выплаты начисляются по ставке 8% годовых. Каким будет размер фонда к концу третьего года?

Решение. Проценты на выплаты фонда начисляются по ставке 8% годовых или 4% полугодовых, поэтому, чтобы к концу пятого года фонд содержал 100000 у.е., величина выплат должна быть равна (4.3.3):

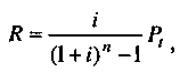
Проценты на долг в конце каждого полугодия составляют 6% от 100000 у.е., то есть 6000 у.е. Полный годовой расход по долгу составляет:

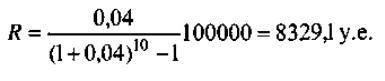
В конце третьего года фонд содержит из формулы (4.3.4):

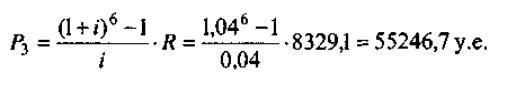
Ясно, что рассматриваемый способ погашения долга — созда­ние фонда— выгоден должнику только тогда, когда проценты по ставке больше, чем процент выплат за долг.