
- •Задание для самостоятельной работы по теме: "способы обработки экспериментального материала".
- •1. Правила построения таблиц.
- •2. Основные назначения графиков.
- •3. Правила построения графиков
- •4. Правила округления чисел.
- •5. Погрешности измерений.
- •А. Ошибки прямых измерений.
- •Тема № 2
- •Тема № 3
- •Лабораторная работа №1 «Определение константы калориметра по известному тепловому эффекту процесса»
- •Тема № 4
- •I. Мотивация цели:
- •Лабораторная работа№2
- •Тема № 5
- •Лабораторная работа №3
- •Тема № 7
- •Примеры решения задач
- •Решение.
- •Решение:
- •Тема № 8
- •Примеры решения задач
- •Решение
- •Лабораторная работа №10
- •Примечания:
- •Тема №9 свойства буферных растворов
- •I план изучения темы
- •V Лабораторная работа
- •1. Зависимость рН буферного раствора от соотношения концентраций компонентов и от разведения.
- •1) Приготовить три ацетатных буферных раствора с различным соотношением концентраций компонентов.
- •VI. Литература:
- •Тема №10 буферная емкость
- •I план изучения темы
- •VI. Литература:
- •Тема №11 формальная химическая кинетика
- •Лабораторная работа
- •Тема №12 кинетика химических реакций различных порядков
- •Лабораторная работа
- •Тема №13 влияние температуры на скорость химической реакции.
- •Лабораторная работа
- •Тема №14 основы фармакокинетики
- •I. План
- •II. Цель самоподготовки
- •VI. Литература.
Тема № 4
ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ. ЭНТРОПИЯ И ЕЕ ИЗМЕНЕНИЕ В РАЗЛИЧНЫХ ПРОЦЕССАХ
I. Мотивация цели:
Второй закон термодинамики – закон о возможности протекания самопроизвольных процессов. Он устанавливает критерии необратимости термодинамических процессов. На его основании можно предсказать, при каких внешних условиях возможен процесс и в каком направлении он будет протекать, что представляет большой практический и теоретический интерес.
Третий закон термодинамики – закон об абсолютном значении энтропии, который был сформулирован уже в начале XX столетия. На его основе можно вычислить константу равновесия химической реакции, а, следовательно, и максимально возможный выход продукта реакции, не прибегая к опытному ее определению ни при одной из температур.
II. ЦЕЛЬ САМОПОДГОТОВКИ:
1. Усвоить содержание II и III начал термодинамики, знать их различные характеристики.
2. Научиться рассчитывать абсолютную и стандартную энтропии, изменение энтропии в различных физико-химических процессах.
III. ИСХОДНЫЙ УРОВЕНЬ ЗНАНИЙ:
Понятие о термодинамических функциях состояния, системах, параметрах.
Первый закон термодинамики.
Приемы дифференцирования и интегрирования.
IV. П Л А Н И З У Ч Е Н И Я Т Е М Ы:
1. Самопроизвольный процесс. Признаки самопроизвольного процесса.
2. Равновесные и неравновесные процессы.
3. Обратимые и необратимые процессы. Критерии термодинамически обратимого процесса.
4. Тепловая машина Карно. КПД тепловой машины. Цикл Карно как основа II начала термодинамики.
5. Второй закон термодинамики: словесные формулировки и математические уравнения, его выражающие. Статистическая природа II начала термодинамики.
6. III закон термодинамики. Абсолютная и стандартная энтропии.
7. Тепловая теорема Нернста.
8. Энтропия – определение понятию. Многоплановый смысл и свойства энтропии:
- функция состояния;
- мера «связанной энергии»;
- мера необратимости процесса;
- мера неупорядоченности в системе;
- критерий направленности и предела самопроизвольного процесса в изолированных системах.
9. Связь энтропии с термодинамической вероятностью системы в данном состоянии – уравнение Больцмана. Статистический характер энтропии.
10. Изменение энтропии в обратимом и необратимом процессах для изолированной и неизолированной систем.
11. Расчет изменения энтропии в различных процессах.
12. Связь I и II законов термодинамики.
V. ЛИТЕРАТУРА:
А.П. Беляева и др. Физическая и коллоидная химия. М.: ГЭОТАР-Медиа, 2008, с. 53-63.
Евстратова К. И., Купина Н. А., Малахова Е.Е. Физическая и коллоидная химия М., 1990, с. 15-18, 35-42.
Киреев В. А. Краткий курс физической химии М. 1978, с. 202-217.
К.С. Краснов Физическая химия. - М., Высшая школа, 2001, с. 235-241, 251-260.
Стромберг А. Г., Семченко Д.П. Физическая и коллоидная химия, М. 1999, с. 81-93.
Лекционный материал
VI. В О П Р О С Ы Д Л Я С А М О К О Н Т Р О Л Я:
1. Дайте определение энтропии, исходя из соотношения
![]()
2. Напишите математическое соотношение между изменением энтропии и теплотой необратимого процесса, протекающего в неизолированной системе.
3. Как изменяется энтропия в изолированной системе при самопроизвольном течении процесса?
4. В каком соотношении находятся молярные энтропии трех агрегатных состояний одного вещества: газа, жидкости и твердого тела?
5. В изолированной системе самопроизвольно протекает химическая реакция с образованием некоторого количества конечного продукта. Как изменяется энтропия системы?
6. Как изменяется энтропия:
а) при кристаллизации 1 моль жидкой воды;
б) при плавлении 1 моль льда;
в) при нагревании 1 моль воды от 20 ОС до 50 ОС.
7. Приведите уравнение для расчета изменения энтропии 1 моль бензола при нагревании его от 0 ОС до 20 ОС. Температура плавления бензола 5,5 ОС.
8. Как изменяется энтропия изолированной системы, в которой обратимо кристаллизуется вещество?
9. Дайте определение:
а) абсолютной энтропии;
б) стандартной энтропии.
10. Приведите уравнение Больцмана, устанавливающее связь между энтропией и термодинамической вероятностью состояния системы.
11. Приведите толкование понятия "связанная энтропия" (TS).
12. Как изменяется связанная энергия системы TS при:
а) нагревании газа;
б) при конденсации водяного пара в жидкость?
Ответ обосновать.
13. К какому значению стремится энтропия правильно образованного кристалла при приближении температуры к абсолютному нулю.
14. Напишите математическое выражение второго закона термодинамики для бесконечно малого изменения состояния в обратимом и необратимом процессах, протекающих в неизолированной системе.
VII. ОБЯЗАТЕЛЬНЫЕ ДЛЯ ВЫПОЛНЕНИЯ ЗАДАНИЯ:
Примеры решения задач
Пример 4-1 Рассчитайте изменение энтропии при нагревании 0.7 моль моноклинной серы от 25 до 200 оС при давлении 1 атм. Мольная теплоемкость серы равна:
Cp(Sтв) = 23.64 Дж/(моль. К), Cp(Sж) = 35.73 + 1.17. 10-3. T Дж/(моль. К).
Температура плавления моноклинной серы 119 оС, удельная теплота плавления 45.2 Дж/г.
Решение. Общее изменение энтропии складывается из трех составляющих: 1) нагревание твердой серы от 25 до 119 оС, 2) плавление, 3) нагревание жидкой серы от 119 до 200 оС.
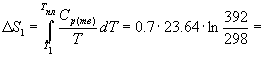 4.54
Дж/К.
4.54
Дж/К.
![]() 2.58
Дж/К.
2.58
Дж/К.
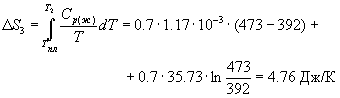
![]() S
=
S1
+
S2
+
S3
= 11.88 Дж/К.
S
=
S1
+
S2
+
S3
= 11.88 Дж/К.
Ответ. 11.88 Дж/К.
Пример 4-2. Найдите изменение энтропии газа и окружающей среды, если n молей идеального газа расширяются изотермически от объема V1 до объема V2: а) обратимо; б) против внешнего давления p.
Решение. а) Изменение энтропии газа при обратимом изотермическом расширении можно найти с помощью термодинамического определения энтропии с расчетом теплоты расширения по первому закону:
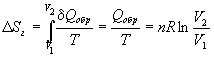 .
.
Так как расширение обратимое, то общее изменение энтропии Вселенной равно 0, поэтому изменение энтропии окружающей среды равно изменению энтропии газа с обратным знаком:
![]() .
.
б) Энтропия - функция состояния, поэтому изменение энтропии системы не зависит от того, как совершался процесс - обратимо или необратимо. Изменение энтропии газа при необратимом расширении против внешнего давления будет таким же, как и при обратимом расширении. Другое дело - энтропия окружающей среды, которую можно найти, рассчитав с помощью первого закона теплоту, переданную системе:
![]() .
.
В этом выводе мы использовали тот факт, что U = 0 (температура постоянна). Работа, совершаемая системой против постоянного внешнего давления равна: A = p(V2-V1), а теплота, принятая окружающей средой, равна работе, совершенной системой, с обратным знаком.
Общее изменение энтропии газа и окружающей среды больше 0:
![]() ,
,
как и полагается для необратимого процесса.
Пример 4-3.Расчитайте изменение энтропии 1000 г воды в результате ее замерзания при -5 ОС. Теплота плавления льда при 0оС равна 6008 Дж/моль. Теплоемкости льда и воды равны 34.7 и 75.3 Дж/(моль. К), соответственно. Объясните, почему энтропия при замерзании уменьшается, хотя процесс - самопроизвольный.
Решение. Необратимый процесс замерзания воды при температуре -5 ОС можно представить в виде последовательности обратимых процессов: 1) нагревание воды от -5 ОС до температуры замерзания (0 ОС); 2) замерзание воды при 0 ОС; 3) охлаждение льда от 0 до -5 ОС:
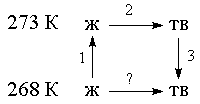
Изменение энтропии в первом и третьем процессах (при изменении температуры) рассчитывается по формуле (4.9):
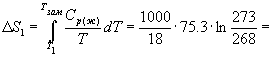 77.3
Дж/К.
77.3
Дж/К.
 -35.6
Дж/К.
-35.6
Дж/К.
Изменение энтропии во втором процессе рассчитывается как для обычного фазового перехода (4.13). Необходимо только иметь в виду, что теплота при замерзании выделяется:
![]() -1223
Дж/К.
-1223
Дж/К.
Т.к. энтропия - функция состояния, общее изменение энтропии равно сумме по этим трем процессам:
S = S1 + S2 + S3 = -1181 Дж/К.
Энтропия при замерзании убывает, хотя процесс самопроизвольный. Это связано с тем, что в окружающую среду выделяется теплота и энтропия окружающей среды увеличивается, причем это увеличение больше, чем 1181 Дж/К, поэтому энтропия Вселенной при замерзании воды возрастает, как и полагается в необратимом процессе.
Ответ. -1181 Дж/К.
4-1. Приведите пример термодинамического процесса, который может быть проведен как обратимо, так и необратимо. Рассчитайте изменение энтропии системы и окружающей среды в обоих случаях.
4-2. Рассчитайте изменение энтропии при образовании 1 м3 воздуха из азота и кислорода (20 об.%) при температуре 25 оС и давлении 1 атм.
4-3. Рассчитайте мольную энтропию неона при 500 К, если при 298 К и том же объеме энтропия неона равна 146.2 Дж/(моль. К).
4-4. Рассчитайте изменение энтропии при нагревании 11.2 л азота от 0 до 50 оС и одновременном уменьшении давления от 1 атм до 0.01 атм.
4-5. Один моль гелия при 100 оС и 1 атм смешивают с 0.5 моль неона при 0 оС и 1 атм. Определите изменение энтропии, если конечное давление равно 1 атм.
4-64-7. Три моль идеального одноатомного газа (CV = 3.0 кал/(моль. К)), находящегося при T1 = 350 K и P1 = 5.0 атм, обратимо и адиабатически расширяются до давления P2 = 1.0 атм. Рассчитайте конечные температуру и объем, а также совершенную работу и изменение внутренней энергии, энтальпии и энтропии в этом процессе.
4-8. Рассчитайте изменение энтропии при нагревании 0.4 моль хлорида натрия от 20 до 850 оС. Мольная теплоемкость хлорида натрия равна:
Cp(NaClтв) = 45.94 + 16.32. 10-3. T Дж/(моль. К), Cp(NaClж) = 66.53 Дж/(моль. К).
Температура плавления хлорида натрия 800 оС, теплота плавления 31.0 кДж/моль.
4-9. Рассчитайте изменение энтропии при смешении 5 кг воды при 80 оС с 10 кг воды при 20оС. Удельную теплоемкость воды принять равной: Cp(H2O) = 4.184 Дж/(г. К).
4-10. Рассчитайте изменение энтропии при добавлении 200 г льда, находящегося при температуре 0 оС, к 200 г воды (90 оС) в изолированном сосуде. Теплота плавления льда равна 6.0 кДж/моль.
4-11. Запишите выражение для расчета абсолютной энтропии одного моль воды при температуре 300 0С и давлении 2 атм.
4-12. Нарисуйте график зависимости стандартной энтропии воды от температуры в интервале от 0 до 400 К.
4-13. Рассчитайте изменение энтропии 1000 г метанола в результате его замерзания при -105 ОС. Теплота плавления твердого метанола при -98 оС (т.пл.) равна 3160 Дж/моль. Теплоемкости твердого и жидкого метанола равны 55.6 и 81.6 Дж/(моль. К), соответственно. Объясните, почему энтропия при замерзании уменьшается, хотя процесс - самопроизвольный.
4-14.Пользуясь справочными данными, рассчитайте стандартное изменение энтропии в реакции H2(г) + ЅO2(г) = H2O(г) а) при 25 оС; б) при 300 оС.
4-15. Теплоемкость некоторого вещества в интервале температур от T1 до T2 изменяется следующим образом:
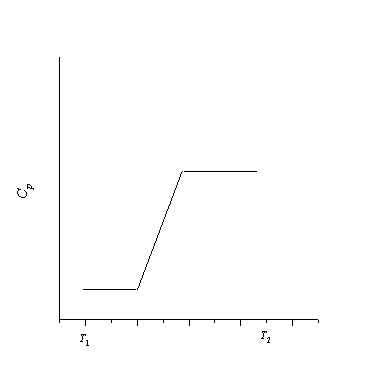
Постройте график зависимости энтропии вещества от температуры в этом интервале температур.
4-16. Пользуясь справочными данными, приведите пример самопроизвольной химической реакции, для которой стандартное изменение энтропии меньше 0.
VIII. ПЛАН РАБОТЫ НА ПРЕДСТОЯЩЕМ ЗАНЯТИИ:
1. Контроль и коррекция выполнения домашнего задания.
2. Разбор основных теоретических вопросов темы.
3. Решение задач.
4. Тестовый контроль.
5. Выполнение лабораторной работы “Определение теплоты растворения хорошо растворимой соли”
