§5.4. Модифицированный критерий Стьюдента (парный t-тест) сравнения выборочных средних двух зависимых выборок

Модифицированный критерий Стьюдента.

Пусть из двух генеральных совокупностей Х и Y, имеющих распределение, близкое к нормальному, извлечено по одной выборке одинаковых объемов, варианты в которых попарно зависимы. Такие выборки называются зависимыми.

Поскольку обычно х_iу_i (i=1,…n), то необходимо установить, являются ли значимыми различия между результатами попарно зависимых измерений х_i и у_i. Значимость различия между ними определяется с помощью модифицированного критерия Стьюдента.

Рассматриваемый в этом параграфе критерий применяется для сравнения двух методов исследования, осуществляемых одной лабораторией, или сравнения результатов исследований, проведенных одним и тем же методом, но в разных лабораториях.

Разность (расхождение) наблюдаемых величин обозначается через d_i=х_iу_i, тогда среднее расхождений равно . Требуется проверить основную гипотезу Н₀: =0 при альтернативной гипотезе Н₁: ¹0.

Наблюдаемое значение модифицированного критерия Стьюдента вычисляется по формуле:

, (4.5)

где величина называется ошибкой средней разности и вычисляется по формуле:

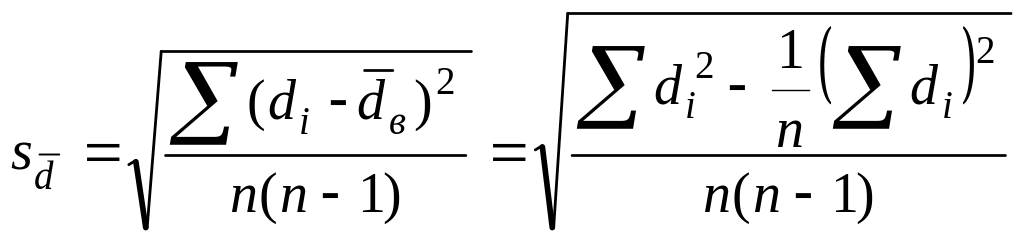, (4.6)

где объем выборки n=n_х=n_у, d_i=х_iу_i, суммирование проводится по всем парам наблюдений.

Правило принятия решения при использовании модифицированного критерия Стьюдента.

По таблице критических точек распределения Стьюдента (или вычисляется в Excel) для заданного уровня значимости a и числа степеней свободы распределения Стьюдента, равного

k=n-1, (4.7)

находится критическая точка двусторонней критической области t_a(k). Это значение сравнивается с наблюдаемым значением критерия :

• если <t_a(k), то нет оснований отвергнуть основную гипотезу, то есть результаты измерений различаются незначимо;

• если ³t_a(k), то основная гипотеза отвергается, то есть различие между результатами измерений признается существенным, систематическим.

Сравнение средних двух зависимых выборок в Excel.

Проверка значимости различия между результатами попарно зависимых измерений по модифицированному критерию Стьюдента (4.5) осуществляется в Excel с помощью инструмента анализа Парный двухвыборочный t-тест для средних. Для его вызова следует выполнить команду СервисАнализ данных. В появившемся диалоговом окне Анализ данных выбрать инструмент Парный двухвыборочный t-тест для средних и нажать ОК. В появившемся диалоговом окне с названием выбранного инструмента анализа порядок заполнения точно такой же, как и в диалоговых окнах для t-тестов независимых выборок, описанных в предыдущем параграфе. После заполнения всех необходимых полей этого окна и нажатия на кнопку ОК появится таблица с названием Парный двухвыборочный t-тест для средних, в которой будут содержаться результаты вычислений.

Данный тест вычисляет средние и дисперсии обеих выборок, их объемы, коэффициенты корреляции (в строке: Корреляция Пирсона), число степеней свободы (4.7) (в строке: df), наблюдаемое значение модифицированного критерия Стьюдента (4.5) (в строке: t-статистика), остальные строки называются также как и в таблицах t-тестов независимых выборок, описанных в предыдущем параграфе.

Вычисленное в этом тесте наблюдаемое значение критерия (4.5), находящееся в строке t-статистика, сравнивается с критической точкой распределения Стьюдента, находящееся в строке t критическое двухстороннее (для двухсторонней критической области), а затем принимается решение согласно указанному выше правилу.