Гомоморфизмы алгебр

def. Пусть и – однотипные алгебры, - главная операция алгебры , а 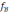– соответствующая ей главная операция алгебры , (т.е. и имеют одинаковые ранги).

, где n – ранг операции

( ) – тип алгебры

( ) – тип алгебры

def. Отображение h основного множества А в основное множество В, сохраняет главную операцию алгебры , если для ( )

, где n – ранг операции . ( )

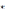
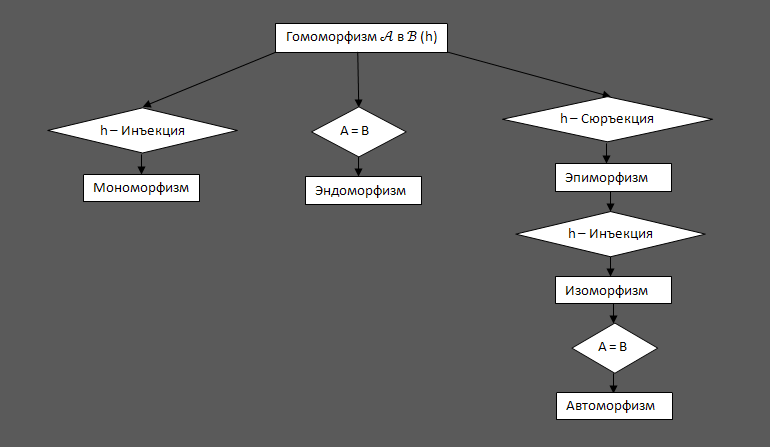
def. Гомоморфизмом алгебры в (на) однотипную алгебру называют такое отображение h множества в (на) множество , которое сохраняет все главные операции алгебры , т.е. для любой операции алгебры выполняется условие ( ).

def. Гомоморфизм алгебры на алгебру называется эпиморфизмом.

def. Гомоморфизм h алгебры на алгебру называют изоморфизмом, если h есть инъективное отображение множества на множество . При этом пишут .

def. Гомоморфизм h алгебры в алгебру , называется мономорфизмом, если h является инъективным отображением множества в множество .

def. Гомоморфизм алгебры в себя, называется эндоморфизмом.

def. Изоморфизм алгебры 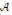на себя, называется автоморфизмом.

Пример 1. Дано отображение

h: .

Выяснить, является ли h гомоморфизмом. Если да, то какой это частный случай?

Решение:

Пример 2. Дано отображение

, .

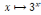
Булевы алгебры

def. Алгебра типа (2,2,1,0,0) называется булевой алгеброй, если выполняются следующие условия (аксиомы):

А1. Существуют нейтральные элементы относительно бинарных операций соответственно, т.е.

,

.

А2. Операции ассоциативны, т.е.

,

.

A3. Операции коммутативны, т.е.

, .

А4. Операции дистрибутивны относительно друг друга, т.е.

,

A5. , .

Замечание. Аксиома А5 может побудить к ошибочному заключению о том, что 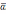является симметричным элементом к , однако это не так. Если бы был симметричным элементом к , то и

def. Результат операции называется суммой, а сама операция – сложением

Результат операции называется произведением, а операция – умножением.

Результат операции и сама операция называется дополнением.

Разные авторы в литературе операции умножения и сложения обозначаются по-разному:

+

def. Для любого выражения булевой алгебры определяется дуализм (двойственное выражение), как выражение, полученное из исходного, заменой н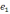а *, * на ,

на , на .

Каждая из аксиом булевой алгебры - эта пара аксиом. Внутри каждой пары, каждая аксиома является дуализмом по отношению к другой.

Примеры булевых алгебр

1. Двоичная алгебра логики.

Это наиболее простая из булевых алгебр и наиболее важная для компьютерной науки.

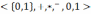, где

0	1
1	0

	0	1
0	0	0
1	0	1

+	0	1
0	0	1
1	1	1