Алгебраические операции и их свойства Бинарные и n-местные алгебраические операции.

Пусть А – непустое множество.

def. Бинарной алгебраической операцией на множестве А называется отображение множества А×А в А.

Обычное сложение и умножение целых чисел являются примерами бинарных операций на множестве.

Пусть Р(М) – множество всех подмножеств множества М, объединение и пересечение 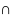– примеры бинарных операций на множестве Р(М).

Пусть f – производная бинарная операция на множестве А. Если при отображении f, элемент а соответствует паре (а,b), то вместо записи f (a,b) = c пишут так же (a,b) с и элемент с называют композицией элементов a и b.

Замечание. Операция, заданная на множестве А будет являться бинарной алгебраической операцией на множестве А, если каждой паре элементов из множества А соответствует единственный элемент того же множества.

def. Пусть Аⁿ есть n-ая степень непустого множества А, где n N. Отображение множества Аⁿ в А называется n-местной операцией на множестве А, а число n - рангом операции. Нульместной операцией на множестве А называется выделение (фиксация) какого-нибудь элемента множества А. Число 0 называется рангом нульместной операции.

def. Отображение из множества Аⁿ в А называется частичной n-местной операцией на А, если область определения отображения не совпадает с Аⁿ.

Операции ранга 0, 1, 2 называют нульарной (нульместной), унарной и бинарной соответственно. Унарную операцию называют так же оператором.

Примеры.

1) Отображение, ставящее в соответствие каждому множеству А из Р(М) его дополнение М \ А, есть унарная операция на множестве Р(М).

2) В области натуральных чисел вычисление не всегда возможно. Поэтому вычисление на множестве натуральных чисел есть частичная бинарная операция.

3) Операция деления рациональных чисел есть частичная бинарная операция на множестве рациональных чисел.

4) Операция, ставящая в соответствие каждому кортежу натуральных чисел наибольший общий делитель этих чисел, является n-местной операцией на множестве натуральных чисел.

Для обозначения n-местной операции обычно используют ту же форму записи, что и для произвольных отображений (функций). Если f есть n-местная операция на множестве А и ((a₁, …, a_n), a_n+1) f, то пишут a_n+1 = f (a₁, …, a_n) и говорят, что a_n+1 – значение операции f для набора аргументов a₁,…, a_n.

Свойства бинарных операций

Пусть и ◦ - произвольные бинарные операции на множестве А.

def. Бинарная операция называется коммутативной, если для любых a, b из А выполняется равенство a b = b a.

def. Бинарная операция называется ассоциативной, если для любых элементов

a, b, c из А выполняется равенство a (b c) = (a b) c.

def. Бинарная операция называется дистрибутивной относительно бинарной операции ,если для любых a, b, c из А выполняются равенства

(a b) ◦ c = (a ◦ c) (b ◦ c) и c ◦ (a b) = (c ◦ a) (c ◦ b).

Если операция ассоциативна, то можно опускать скобки и писать a b c вместо a (b c) или (a b) c.

Примеры.

1) Сложение и умножение рациональных чисел являются коммутативными и ассоциативными бинарными операциями.

2) Операция вычитания на множестве рациональных чисел не коммутативна и не ассоциативна.

3) Операции объединения и пересечения подмножеств множества А коммутативны и ассоциативны на множестве Р(М).

4) Композиция функций есть ассоциативная операция. Композиция функций не коммутативна: в общем случае равенство f ◦ g = g ◦ f не выполняется.

5) На множестве Р(М) подмножеств некоторого множества, операции объединения и пересечения взаимно дистрибутивны друг относительно друга.

6) Умножение целых чисел дистрибутивно относительно сложения. Однако сложение целых чисел не дистрибутивно относительно умножения, так как в общем случае равенство a + b c = (a + b) (a + c) не выполняется.

7) Сложение квадратных матриц порядка n коммутативно и ассоциативно. Умножение квадратных матриц дистрибутивно относительно сложения.

8) Умножение матриц ассоциативно, не коммутативно, умножение матриц дистрибутивно относительно сложения, то есть A (B C) = A B + A C, если произведение А В и сумма В + С существует, и (В + С) А = В А + С А, если произведение В А и сумма В + С существует.