Дм. Лекция № 5 Отображения (функции)

def. Бинарное отношение ƒ называется функцией(отображением), если для любых x,y,z из того, что (x,y) ∈ƒ и (x,z) ∈ƒ, следует, что y = z.

Другими словами, отношение ƒ является функцией, если для любого x из области определения отношения ƒ существует единственное y, такое что (x,y) ∈ƒ. Этот единственный элемент y обозначается через ƒ(x) и называется значением функции ƒ для аргумента x. Если (x,y) ∈ƒ, то используется общепринятая запись y = ƒ(x), а также запись ƒ: x → y.

def. Областью определения функции ƒ называется множество

ƒ={x|∃ y ((x,y) ∈ƒ)}.

def. Областью значений функции ƒ называется множество

ƒ={y|∃ x ((x,y) ∈ƒ)}.

def. Две функции ƒ и g называют равными, если ƒ и g равны как множества, т.е.

( x,y) (x,y) ∈ƒ ⇔(x,y) ∈ g.

def. Функции называются также отображениями. Если функция ƒ задана на паре множеств A и B, т.е. ƒ ⊆AB, то говорят, что ƒ есть отображение из A в B. Если при этом A = Dom ƒ и Im ƒ ⊆B, то говорят, что ƒ есть отображение множества

A в B, и записывают в виде ƒ: A → B. Если A = Dom ƒ и B = Im ƒ, то говорят, что ƒ есть отображение множества A на B.

def. Образом множества C при отображении ƒ называется множество

ƒ(C)= { ƒ (x)| x ∈ C}.

def. Прообразом множества M при отображении ƒ называется множество

= { x ∈ Dom ƒ | ƒ(x) ∈ M}, т.е. множество всех тех элементов из области определения функции ƒ, для которых ƒ(x) ∈ M.

def 1. Функция ƒ называется инъективной, если для любых x,y (из Dom ƒ) из условия ƒ(x)= ƒ(y) следует, что x = y (∀x,y ∈ Dom ƒ | ƒ(x) = ƒ(y) ⇒ x = y).

Из определения следует, что функция ƒ инъективна тогда и только тогда, когда для любых x,y (из Dom ƒ), если x ≠ y, то ƒ(x) ≠ ƒ(y), т.е. для различных аргументов функция ƒ принимает различные значения (∀x,y ∈ Domƒ| x ≠ y ⇒ƒ(x) ≠ ƒ(y)).

def 2. Инъективным отображением называется отображение ƒ: X Y, если оно переводит разные элементы множества X в разные элементы множества Y.

def 1. Функция ƒ, заданная на паре множеств A и B, называется сюръективной, если ƒ есть отображение множества A на B, т.е. ƒ(A) = B (или каждый элемент множества B имеет по крайней мере один прообраз в множестве A).

def 2. Сюръективным отображением называется отображение ƒ: X Y, если в каждый элемент множества Y переходит хотя бы один элемент множества X.

def. Функция ƒ называется биективной (взаимно-однозначным соответствием или отображением), если она одновременно сюръективна и инъективна.

Отображение X Y взаимно однозначно тогда и только тогда, когда каждому элементу множества x, сопоставляется единственный элемент множества y, и обратно – каждый элемент множества y сопоставляется единственному элементу множества x.

Упражнения

1. На рисунке изображены графы различных соответствий. Какие из этих соответствий являются отображениями? Найдите для каждого соответствия его область определения и область значений.

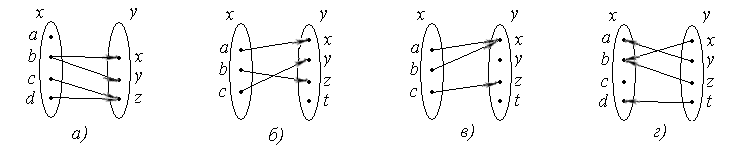
2. Какие из соответствий, графы которых изображены на рисунке, являются:

a) инъективными; б) сюръективными; в) биективными.