Дм. Лекция № 3 Тема: «Отношения»

Def: N-местным отношением P на множествах A₁, A₂ … A_n называется любое подмножество декартового произведения A₁ × A₂ × …× A_n.

При n = 1 отношение P называется унарным (одноместным) и является подмножеством множества A₁. При n = 2 отношение называется бинарным (или двуместным) и является подмножеством декартового произведения A₁ × A₂.

Бинарные отношения

Вообще бинарным отношением называется любое множество упорядоченных пар. Если P – бинарное отношение и 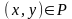, то говорят, что элемент х находится в отношении P к элементу у, или что для элементов х и у выполняется отношение Р, или что х и у связаны отношением Р. Вместо записи часто используют более простую – .

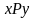Def: Областью определения бинарного отношения P называется множество всех первых элементов упорядоченных пар, входящих в это отношение:

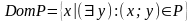
Def: Областью определения бинарного отношения P называется множество всех вторых элементов упорядоченных пар, входящих в это отношение:

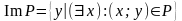
Если 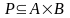, то говорят, что Р есть отношение между элементами множеств А и В или что Р определено на паре множеств А и В.

Def: Если 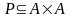(декартов квадрат), то говорят, что Р есть бинарное отношение на множестве А.

Def: Для любого множества А отношение 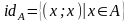называется тождественным отношением или диагональю, а 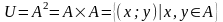- полным отношением или полным квадратом.

Def: Два отношения Р и S называются равными (Р=S), если для любых х, у тогда и только тогда, когда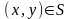 , то есть Р и S равны как множества.

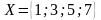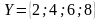Пример 1. На паре множеств и определено отношение 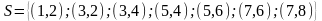. Показать, что 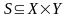, указать область определения и область значения этого отношения.

Решение.

Способы задания бинарных отношений

1. Перечисление входящих в отношение элементов (см. пример 1).

2. С помощью характеристического свойства. Например, два целых числа X и Y связаны отношением P, если X - Y делится на 2.

3. С помощью графика.

Def: Графиком бинарного отношения P называется множество всех точек с координатами (x,y) в плоскости xOy.

4. Ориентированным графом.

Def: Графом называется фигура на плоскости, состоящая из конечного числа точек – вершин графа – и линий, соединяющих некоторые из вершин. Линия, соединяющая какие-либо две вершины графа, называется ребром графа. Линии могут быть прямыми или кривыми. Точки пересечения некоторых ребер графа могут не являться вершинами графа. Граф, на котором указаны стрелками направления его ребер, называется ориентированным.

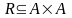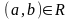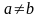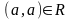Существует простой способ представления бинарных отношений на конечных множествах ориентированными графами. Пусть А – непустое конечное множество и R – бинарное отношение на А, то есть . Представим элементы множества А точками на плоскости. Каждой паре при поставим в соответствие ориентированное ребро, идущее от точки a к точке b. Паре поставим в соответствие петлю с фиксированным направлением обхода (например, всегда против часовой стрелки):

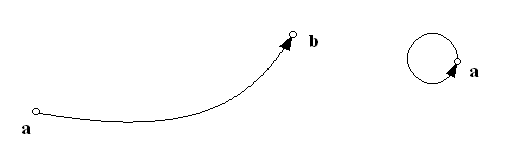
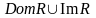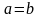Таким образом, бинарному отношению R ставится в соответствие следующая геометрическая фигура: точки плоскости, представляющие элементы множества , ориентированные ребра – каждой паре ставится в соответствие ориентированное ребро, идущее от точки a к точке b, или петля, если . Такая геометрическая фигура называется ориентированным графом отношения R или просто графом отношения R.

Каждое бинарное отношение на конечном множестве можно представить ориентированным графом. С другой стороны, каждый ориентированный граф представляет бинарное отношение на множестве его вершин.

Пример 2. Построить граф отношения: .

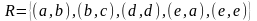Решение.