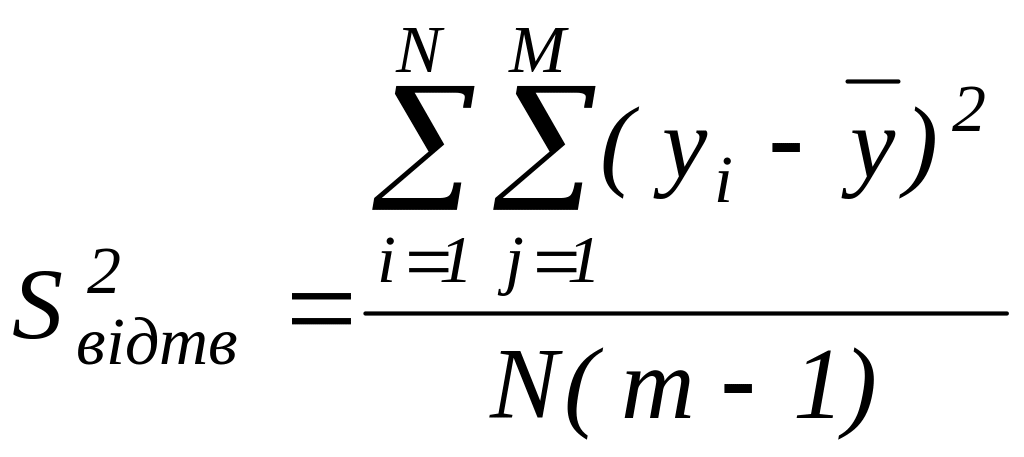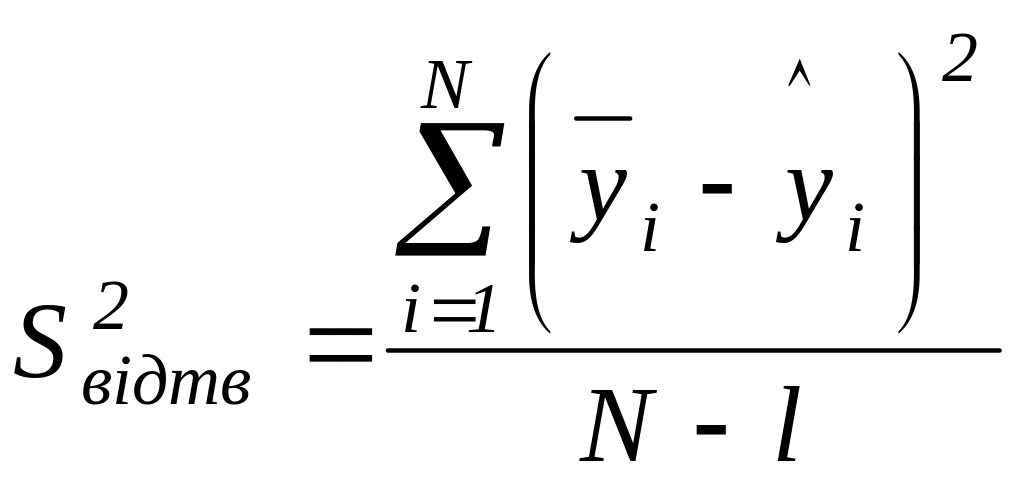3 Реалiзацiя експеримента
Як приклад, розглянемо проведення досліду для наведеної вище матриці (табл. 6.1). Припустимо, що вхідні параметри складу стічної води визначаються факторами Х1 і Х2, а параметр керування позначено фактором Х3.
4 Визначення точності експеримента
В кожному досліді відхилення значень, що отримані, повинні бути мінімальними, тобто виміри параметрів оптимізації мають бути максимально точними.
Для визначення цього відхилення, що характеризується дисперсією, спочатку обчислюється середнє значення параметра оптимізації в кожному досліді:
|
(3) |
де m – кількість повторень в даному досліді;
i – порядковий номер досліду в матриці.
|
(4) |
Результати кожного досліду повинні бути вимірені з однаковою точністю. Для перевірки цього зазвичай використовують припущення про однорідність дисперсій параметра оптимізації. Перевірка гіпотези однорідності дисперсій здійснюється за допомогою критерiя Кохрена, який є відношенням максимальної дисперсії в дослідах до суми всіх дисперсій експеримента:
|
(5) |
де
![]() - максимальне значення вибipкової
диспеpсiї.
- максимальне значення вибipкової
диспеpсiї.
Якщо дисперсiї однорiднi, то
Gmax<Gp(N,m-1), |
(6) |
де Gp(N, m-1) табульоване значення критерiя Кохрена при рiвнi значимостi р (зазвичай його приймають 5%).
Математична модель процеса очистки подається у вигляді полінома:
|
(7) |
де xi,xj – фактори;
b0, bi, bij, - коефіцієнти полінома.
Як перше наближення для рівняння регресії зазвичай використовується поліном неповного другого ступеня. Якщо воно не відповідає реальному процесу очистки стічних вод, тобто не адекватне йому, здійснюється побудова моделі, яка описується поліномом другого рівня. Якщо не адекватне і це рівняння, то будують рівняння більш високих степеней.
Розрахунок коефіцієнтів регресії лінійних членів полінома здійснюється за формулою:
|
(8) |
де
![]() - середне значення параметра
оптимізації в досліді.
- середне значення параметра
оптимізації в досліді.
|
(9) |
де xi - кодоване значення фактора в і-му досліді.
Коефіцієнти регресії, які характеризують взаємодію факторів (ефектів подвійної взаємодії), визначаються за формулою:
|
(10) |
Коефіцієнти регресії, які характеризують ефекти потрійної взаємодії, визначаються за формулою:
|
(11) |
Визначення значимості коефіцієнтів регресії
Значимість
коефіцієнтів регресії перевіряється
порівнянням їх величини із значенням
довірчих інтервалів
![]() ,
які для варіанту планування
експерименту, що разглядається, однакові
для всіх коефіцієнтів.
,
які для варіанту планування
експерименту, що разглядається, однакові
для всіх коефіцієнтів.
Для оцiнки значимостi коефiцiєнтiв рiвняння регресiї (7) необхiдно спочатку знайти дисперсiю вiдтворення. Якщо дисперсiї однорiднi, то дисперсiя вiдтворення:
|
(12) |
Дисперсія коефіціентів регресії визначається з виразу
|
(13) |
При відоміх дисперсіях довірчий інтервал коефiцiєнтiв рiвняння регресiї дорівнює:
|
(14) |
де
t
- табличне
значення критерія Стьюдента при числі
степеней свободи, з якими визначалось
![]() і вибраному рівні значимості.
і вибраному рівні значимості.
Коефіцієнт регресії рахується значимим, якщо його абсолютне значення перевищує величину довірчого інтервалу.
Перевірка адекватності моделі
Перевірка гіпотези адекватності прийнятої моделі реальному процесу здійснюється за критерієм Фішера:
|
(15) |
де
![]() - дісперсія адекватності;
- дісперсія адекватності;
![]() -
дісперсія відтворення.
-
дісперсія відтворення.
Диспеpсiя адекватності визначається за формулою
|
(16) |
де
![]() - значення
параметра оптимізації, яке отримане
розрахунком з рівняння регресії,
з якого виключени всі незначимі
члени (коефіцієнти регресії, які
визнані незначимими, приймаються
рівними 0 і тому не входять в математичну
модель процеса очистки).
- значення
параметра оптимізації, яке отримане
розрахунком з рівняння регресії,
з якого виключени всі незначимі
члени (коефіцієнти регресії, які
визнані незначимими, приймаються
рівними 0 і тому не входять в математичну
модель процеса очистки).
Якщо значення F , що отримано, менше табличного Fp (f1, f2) для обраного рiвня значимостi р i чисел степенiв свободи f1 = N-1 i f2 = N-l, то гіпотеза адекватності приймається. В іншому випадку застосовується планування другого порядка.
Перевірка необхідності планування другого порядка
Перевірка необхідності планування другого порядка обов'язкова в тому випадку, коли в рівнянні регресії, що отримане, хоча б один коефіцієнт при парних взаємодіях Xi був значимим. Значимість його є достатньою підставою для ствердження про нелінійність математичної моделі.
Необхідність
планування другого порядка оцінюється
по внеску у величину параметра оптимізації
коефіцієнтів полінома другої і
більшої степеней. Оцінка суми коефіцієнтів
при квадратичних і більш високих степенях
визначається за величиною різниці
між вільним членом b0
в
рівнянні регресії і середнім
значенням
![]() ,
яке отримане з додаткових до матриці
дослідів в центрі експеримента.
Додаткові досліди проводяться
при нульових кодованих значеннях всіх
факторів.
,
яке отримане з додаткових до матриці
дослідів в центрі експеримента.
Додаткові досліди проводяться
при нульових кодованих значеннях всіх
факторів.
Значимість різниці оцінюється за критерієм Стьюдента:
|
(17) |
де
![]() -
отримана раніше дісперсія, що характеризує
похибку дослідів.
-
отримана раніше дісперсія, що характеризує
похибку дослідів.
Значення критерія Стьюдента порівнюється з його табличним значенням. Якщо отримане значення критерія менше табличного, приймається гіпотеза про незначність квадратичних членів. Таке рішення дозволяє відмовитись від планування другого порядка і обмежитись поданням рівняння регресії поліномом неповної другої степені (без квадратичних членів).
В іншому випадку виконується планування експерименту другого порядку. Методика такого планування викладена в спеціальній літературі.
Приклад побудови математичної моделі з використанням апарата планування експеримента
Розглядається задача побудови математичної моделі процесу електронейтралізації кислих стічних вод підприємств первинної обробки вовни [4]
Під час дослідів параметром оптимізації була величина рН католіта під час електронейтралізації. Як фактори прийняті такі параметри управління процесом:
Х1 – сила струму, А;
Х2 – відстань між електродами, см;
Х3 – тривалість процеса, хв.
Реалiзацiя експеримента
Для побудови математичної моделі процеса електронейтралізації прийнятий план повного факторного експеримента типу 23, матриця якого наведена в табл. 6.2.
Обрахування значень таблиці починаючи з колонки 7 та інших критерієв доцільно виконувати за допомогою електронної таблиці Excel.
Таблиця 6.2 Матриця, результати і розрахунок планованого факторного експерименту
кодування факторів номер досліду |
сила струму,А |
відстань між електродами,см |
тривалість процесу, хв |
|
|
|
|
|
|
|
х1 |
х2 |
х3 |
У1 |
У2 |
Усер |
S2 |
Yp |
(Ycep-Yp)2 |
верхній рівень |
4 |
8 |
40 |
|
|
|
|
|
|
нульовий рівень |
2,25 |
5 |
25 |
|
|
|
|
|
|
нижній рівень |
0,5 |
2 |
10 |
|
|
|
|
|
|
інтервал |
1,75 |
3 |
15 |
|
|
|
|
|
|
1 |
1 |
1 |
1 |
11,89 |
11,91 |
11,9 |
0,0002 |
12,37 |
0,2180 |
2 |
-1 |
1 |
1 |
4,82 |
4,82 |
4,82 |
0 |
5,38 |
0,3101 |
3 |
1 |
-1 |
1 |
11,82 |
11,83 |
11,825 |
5E-05 |
11,28 |
0,2991 |
4 |
-1 |
-1 |
1 |
5,24 |
4,61 |
4,925 |
0,19845 |
4,38 |
0,2936 |
5 |
1 |
1 |
-1 |
5,92 |
5,54 |
5,73 |
0,0722 |
5,17 |
0,3157 |
6 |
-1 |
1 |
-1 |
4,53 |
4,34 |
4,435 |
0,01805 |
3,86 |
0,3270 |
7 |
1 |
-1 |
-1 |
5,34 |
5,3 |
5,32 |
0,0008 |
5,89 |
0,3270 |
8 |
-1 |
-1 |
-1 |
4,53 |
4,31 |
4,42 |
0,0242 |
5,00 |
0,3386 |
|
|
|
|
|
|
53,375 |
0,31395 |
|
|
Критерій Кохрена |
|
|
|
|
|
|
0,632107 |
|
|
Табличне значення |
|
|
|
|
|
|
0,68 |
|
|
Висновок
На даній роботі ми вивчали теоретичні основи та практично застосовували методику планування експерименту для визначення математичної моделі.
Ми розглянули критерії Стьюдента, Фішера та Кохрена.
Останній з них ми визначали за допомогою допоміжної таблиці Exсel, підставляючи довільні значення в колонки 5 та 6. При цьому змінювалися подальші значення, наведені в тій же таблиці. Відповідно, значення рівняння математичної моделі змінилося.
Після зміни значень, змінився і критерій Кохрена. Він став менше табличного, і задовольнив умову однакової точності проведення паралельних експериментів.

 i=1,2,...n
,
i=1,2,...n
,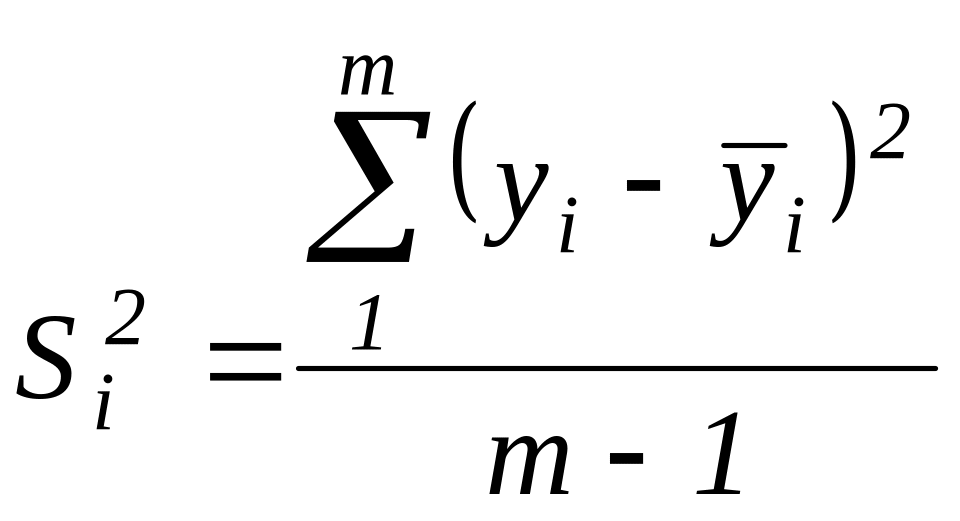
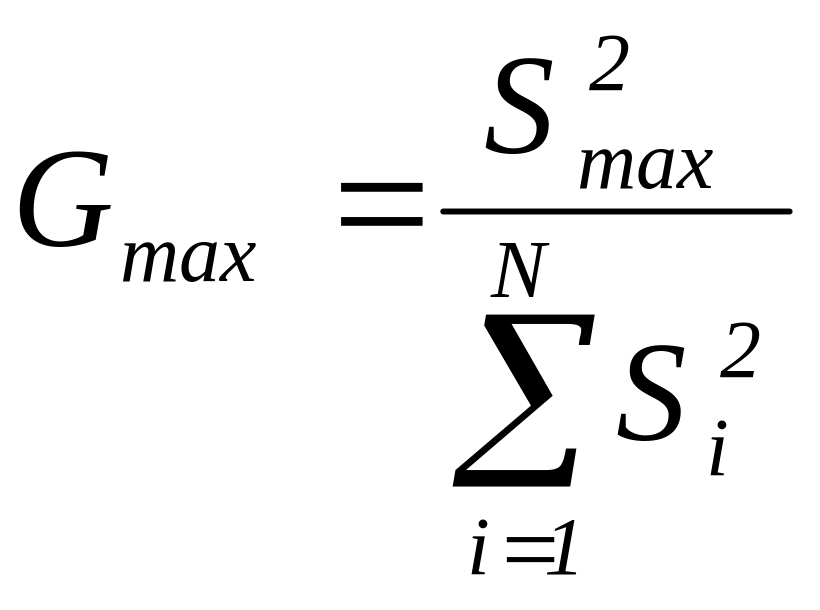
 ,
, ,
,