- •Содержание
- •Введение
- •1. Содержание и порядок выполнения расчетно – графической работы
- •2. Разбор типового задания Техническая постановка задачи
- •Математическая постановка задачи
- •Приведение задачи к канонической форме
- •Нахождение начального опорного плана
- •Постановка l- задачи
- •Решение l- задачи
- •0 Итерация
- •Формирование начального опорного плана исходной злп
- •Решение исходной злп первым алгоритмом симплекс-метода Описание первого алгоритма симплекс-метода
- •Порядок вычислений по первому алгоритму:
- •Решение исходной задачи
- •Формирование м-задачи
- •Решение м-задачи вторым алгоритмом симплекс-метода Описание второго алгоритма симплекс-метода
- •Порядок вычислений по второму алгоритму
- •Решение м-задачи
- •Постановка двойственной задачи
- •Формирование решения двойственной задачи
- •3. Индивидуальные задания
- •Список литературы
Формирование м-задачи
Далеко не всегда имеет смысл разделять решение задачи линейного программирования на два этапа – вычисление начального опорного плана и определение оптимального плана. Вместо этого решается расширенная задача (М-задача). Она имеет другие опорные планы (один из них всегда легко указать), но те же решения (оптимальные планы), что и исходная задача.
Расширенная М-задача применительно к исходной задаче (2.5) – (2.7) записывается следующим образом:
|
(2.24) |
|
(2.25) |
|
(2.26) |
Здесь
![]() - достаточно большое число.
- достаточно большое число.
Начальный
опорный план задачи (2.24) – (2.26) может
быть назначен непосредственно, так как
в матрице условий этой задачи уже
сформирована единичная подматрица,
которая и составит его базис
![]() .
Поэтому вектор
.
Поэтому вектор
![]() с компонентами
с компонентами![]()
![]() ,
,
![]()
![]() и будет являться начальным опорным
планом задачи (2.24) – (2.26).Переменные
и будет являться начальным опорным
планом задачи (2.24) – (2.26).Переменные
![]() называются искусственными
переменными.
называются искусственными
переменными.
Таким образом, исходная задача линейного программирования с неизвестным заранее начальным опорным планом сводится к М-задаче, начальный опорный план которой может быть указан непосредственно. В процессе решения этой расширенной задачи можно либо вычислить оптимальный план задачи (2.5) – (2.7), либо убедиться в её неразрешимости, если оказывается неразрешимой М-задача.
В соответствии с
вышеизложенным составим М-
задачу применительно к нашей ЗЛП (2.15),
(2.16), записанной в канонической форме.
Для этого введём одну искусственную
неотрицательную переменную
![]() и запишем М-задачу
в виде :
и запишем М-задачу
в виде :
|
(2.27) |
|
(2.28) |
где М – сколь угодно большая положительная величина. Считается что она заведомо больше любого числа которыми будут заполняться симплекс-таблицы.
Замечание:
как и в L-задаче,
добавление только одной искусственной
переменной
(вместо четырёх) обусловлено тем, что
исходная задача уже содержит три
единичных вектора условий
![]() .
.
Решение м-задачи вторым алгоритмом симплекс-метода Описание второго алгоритма симплекс-метода
Опишем алгоритм применительно к решению ЗЛП, записанной в канонической форме с односторонними ограничениями:
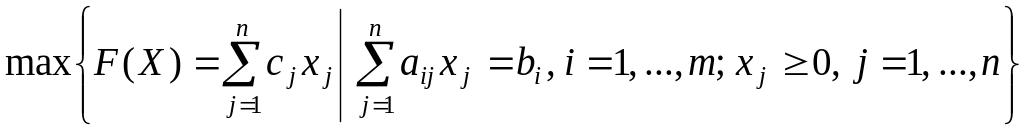
Пусть известен
начальный опорный план
![]() с базисом
с базисом
![]() ,
т.е.
,
т.е.
![]() - базисные компоненты,
- небазисные компоненты.
- базисные компоненты,
- небазисные компоненты.
В данном методе
все параметры итерации, необходимые
для оценки плана на оптимальность и
перехода к лучшему плану, вычисляются
через элементы
![]() обратной матрицы
обратной матрицы
![]() .
Поэтому второй алгоритм симплекс-метода
также называют алгоритмом
обратной матрицы.
.
Поэтому второй алгоритм симплекс-метода
также называют алгоритмом
обратной матрицы.
Вычисления удобно выполнять, используя две симплекс-таблицы:
Основная таблица |
||||||||
№ |
|
P |
|
|
… |
|
|
t |
1 |
|
|
|
|
… |
|
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
|
|
|
|
… |
|
|
|
… |
… |
… |
… |
… |
… |
… |
… |
… |
|
|
|
|
|
… |
|
|
… |
|
|
|
|
|
… |
|
|
|
Вспомогательная таблица |
||||
№ |
|
|
… |
|
1 |
|
|
… |
|
… |
… |
… |
… |
… |
|
|
|
… |
|
|
|
|
… |
|
0 |
|
|
… |
|
1 |
|
|
… |
|
2 |
|
|
… |
|
… |
… |
… |
… |
… |