4.2.Многоленточная мт

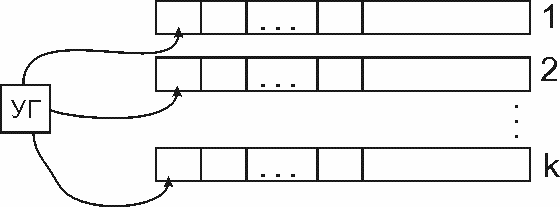
Простым обобщением МТ является k-ленточная МТ. Вместо одной ленты здесь имеется k лент, каждая из которых обслуживается своей головкой. Имеется управляющее устройство, которое и характеризуется определенным состоянием (в случае одноленточной МТ головка и это устройство объединялись в одном объекте). Конфигурация в этом случае состоит из записей на лентах с указанием мест головок и состояния управляющего устройства. Вместо пары конфигурации мы имеем (k+1)-ку из символа текущего состояния и символов в обозреваемых ячейках.

Команды задаются уже отображением SA^kS{A{L, R, St}}^k.

В течение одного такта работы можно изменить состояние, напечатать в обозреваемых ячейках новые символы, если это требуется программой и сдвинуть независимо друг от друга какие-нибудь или все головки в тех направлениях, которые предусмотрены командой.

4.3.Недетерминированная мт

Это совершенно иное обобщение понятия МТ. Рассмотрим случай одноленточной недетерминированной машины Тьюринга (НМТ).

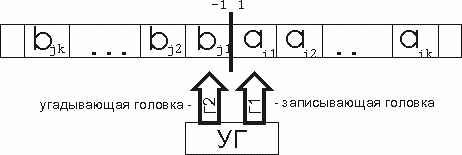
Имеется две управляющие головки (УГ) и одна лента. Одна головка Г1 - обычная, такая же, как в МТ, а вторая Г2, которая часто называется угадывающей, может только записывать. Запись на ленте представляет собой слово (условие задачи), записанное слева направо, начиная с ячейки с номером 1. В начальный момент времени обычная головка наблюдает ячейку с номером 1, а пишущая головка - ячейку с номером (-1). Вначале работает только пишущая (угадывающая) головка. На каждом такте работы она может написать символ в наблюдаемой ячейке и сдвинуться влево, либо остановиться. В последнем случае начинает работать обычная головка с состояния q₀. С этого момента НМТ работает точно так же, как МТ с той лишь разницей, что наблюдает не самый крайний слева символ входного слова.

Управляющее устройство пишущей головки принимает решение совершенно произвольно, поэтому может никогда не остановиться.

Ниже в разного рода определениях важна только возможность написания некоторого слова угадывающей головкой. Так как она пишет произвольно, то может написать любую букву в ячейке с номером -1, любую – в ячейке -2 и т.д. Если мы будем рассматривать все возможные результаты работы угадывающей головки, то это будут все возможные слова в данном алфавите.

Далее мы будем различать входное слово I и слово U, записанное угадывающей головкой.

Разница между МТ и НМТ может быть проиллюстрирована с помощью сравнения модели обычных вычислений и моделью параллельных вычислений.

В качестве примеров можно рассмотреть задачи о выполнимости, о гамильтоновом цикле и о простоте числа.

4.4.Оракульная мт

Как и в предыдущем случае здесь две головки (обычная и оракульная), но и две ленты (обычная и оракульная). Во множестве состояний выделены два особых: состояние вопроса к оракулу q_c и резюмирующее состояние q_r. Обе головки управляются одним управляющим устройством. В начальный момент времени на обычной ленте записано входное слово I, начиная с ячейки с номером 1. Все остальные ячейки обеих лент пусты.

Работа оракульной машины Тьюринга (ОМТ) почти аналогична работе двухленточной МТ. Разница в следующем. Если управляющее устройство оказывается в состоянии q_c, то поведение на следующем шаге зависит от фиксированной оракульной функции g:A*A*.

Этот шаг не изменяет положение основной головки и запись на основной ленте. Его результатом является переход в состояние q_r и изменение за один шаг всего содержимого оракульной ленты по следующему правилу.

Пусть y - слово, записанное на оракульной ленте, начиная с первой ячейки и до ячейки, над которой находится головка. Если головка находится левее ячейки с номером один, то полагается, что y - некоторая заранее оговоренная постоянная. За данный такт на оракульной головке записывается слово g(y), начиная с первой ячейки. Остальная часть ленты стирается, а головка обозревает ее первую ячейку.

То есть мы имеем как бы комбинацию обычной машины Тьюринга М и некоторого оракула g. Вообще говоря, для одной и той же задачи могут быть использованы разные оракулы. Поэтому можно искусственно вычленить ту часть программы ОМТ, которая касается работы обычной головки. Она ведь не касается действий оракульной головки. Именно эту часть программы называют программой ОМТ. Обозначим ее через M. В случае же рассмотрения конкретного оракула g всю программу целиком будем обозначать через M_g, и называть релятивизированной программой ОМТ.