12.3.3.Гипотеза Минского.

Насколько теоретические оценки производительности соответствуют реальности можно проверить, тестируя эти системы. В целом, оценки подтверждаются, отклонения объясняются особенностями систем и тем фактором, что для каждой системы можно придумать задачу, для которой система будет эффективна и наоборот.

В качестве иллюстраций приведем одну гипотезу и экспертную оценку факторов, влияющих на эффективность распараллеливания.

Гипотеза, принадлежащая Минскому, состоит в предположении, что в N-процессорной векторно-параллельной вычислительной системе или MIMD-вычислительной системе, в которой производительность каждого процессора равна единице, общая производительность E растет как logN.

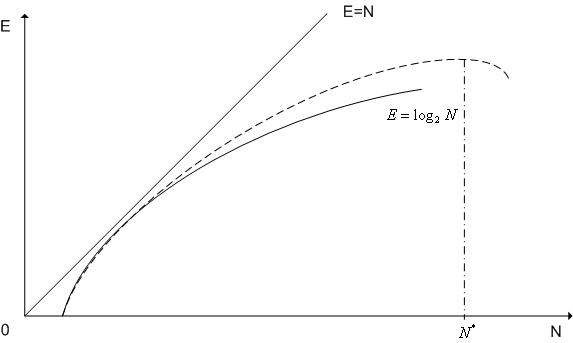
В первых параллельных вычислительных системах, когда количество процессоров было невелико, гипотеза Минского подтверждалась. В современных системах с большим количеством процессоров имеет место зависимость производительности от числа процессоров, показана на рисунке пунктиром. Основные причины такой зависимости:

• с ростом количества процессоров растут коммуникационные расходы (вследствие роста диаметра коммуникационной сети);

• с ростом количества процессоров растет несбалансированность их загрузки.

Таким образом, если количество процессоров системы N превышает величину N*, то целесообразно использовать мультипрограммный режим работы системы.

В заключение приведем мнение экспертов (вообще говоря, очевидное) о факторах, ко­торые влияют на производительность параллельных вычислительных систем.

Соответствие архитектуры системы особенностям задачи. Например, если решается задача, в которой отсутствуют массивы данных, элементы которых могут обрабатываться одно­временно, а каждая следующая операция может выполняться лишь после за­вершения предыдущей, тогда применение мощного векторного суперкомпью­тера ничего не даст.

Соответствие степени критичности ресурсов особенностям задачи. Например, рассмотрим шину, соединяющую микропроцессоры с памятью. Пропускная способность системной шины оказывает большое влияние на пока­затели ускорения и эффективности, особенно если в задаче много обменов дан­ными между процессорами.

Соответствие механизма организации кэш-памяти особенностям задачи. Большое значение имеет кэш-память: ее объем, частота работы, органи­зация отображения основной памяти в кэш-память. Эффективность кэш-памяти очень сильно зависит от типа задачи, в частности, от рабочего множества адресов и типа об­ращений, которые связаны с локальностью вычислений и локальностью исполь­зования данных. Наиболее характерным примером конструкции, обладающей свойством локальности, является цикл. В циклах на каждой итерации выпол­няются одни и те же команды над данными, которые обычно получены на предшествующей операции. Существенное ускорение выполнения циклов дос­тигается путем его размещения его данных в кэш-памяти. Если объема кэш­памяти не хватает, задействуется следующий уровень иерархии памяти, и т.д. Именно кэш-память чаще всего оказывает наиболее существенное влияние на характеристики программ вообще, и распараллеливаемой задачи в частности.

Сбалансированность задачи. В ситуации с распараллеливанием возникает проблема баланса между вычислительными возможностями процессоров и пропускной способностью коммутационной сети. Если последняя является критичной, то именно она определяет накладные расходы - время за­держки передачи сообщения. Оно зависит от латентности (начальной задержки при посылке сообщений) и длины передаваемого сообщения. Повышение производительности может достигаться за счет увеличения параллельно работающих процессоров. При этом основная проблема - органи­зация связи между процессорами. Конечно, самый простой способ коммутации процессоров - использование общей шины. Однако в таких системах даже не­большое увеличение числа процессоров, подключаемых к общей шине, делает ее узким местом. Применяются различные способы преодоления этой проблемы, основан­ные на использовании различных схем коммутации. Если число процессоров и модулей памяти, для связи между которыми используются коммутаторы, велико, в схеме также возможны большие задержки. Уменьшение задержек дости­гается путем подбора наиболее подходящей топологии сети, обеспечивающей уменьшение средней длины пути между двумя узлами системы. Среднюю дли­ну пути можно уменьшить, применяя вместо простой линейки схему в виде кольца или гиперкуба.