ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра повт и ас
Функции алгебры логики
Методические указания к практическим занятиям по курсу «Введение в математическую логику»
Ростов- на- Дону
2011
Составитель О.В. Ляхницкая,
Методические указания предназначены для студентов специальности 090102 «Компьютерная безопасность», 230105 «Программное обеспечение вычислительной техники и автоматизированных систем», 230102 «Автоматизированные системы управления» и преподавателей, ведущих практические занятия по курсу «Введение в математическую логику»; в них содержатся краткие сведения о логических операциях над высказываниями, равносильных формулах алгебры логики, рассматривается понятие двойственности, представлены алгоритмы приведения функций алгебры логики к СДНФ и СКНФ, а также приведены примеры применения алгебры логики в технике.
Рецензент:
Двойственность. Класс самодвойственных функций.
Определение. Функции f*(x1,
..., xn) называется двойственной
к функции f(x1, ..., xn),
если f*(x1, ..., xn)
=
(
1,
...,
n).
Пример 1. Покажем с помощью таблицы истинности, что константа 0 двойственна к 1:
x |
f |
f* |
0 1 |
0 0 |
1 1 |
Функции f(x) = x и g(x) = двойственны сами себе:
x |
f |
f* |
g |
g* |
0 1 |
0 1 |
0 1 |
1 0 |
1 0 |
так
как f*(0)=
(1).
Определение 2. Если f*(x1, ..., xn) = f(x1, ..., xn), то f(x1, ..., xn) называется самодвойственной.
Множество всех самодвойственных функций обозначается через S.
Пример 2. Покажем, что f(x1,x2,x3)=x1x2x3 – самодвойственна.
х1 |
x2 |
x3 |
f |
f* |
0 0 0 0 1 1 1 1 |
0 0 1 1 0 0 1 1 |
0 1 0 1 0 1 0 1 |
0 1 1 0 1 0 0 1 |
0 1 1 0 1 0 0 1 |
Если f*– самодвойственна, то
(
1,
...,
n)
= f(x1, ..., xn),
т.е. на противоположных наборах функция
принимает противоположные значения.
Пример 3. Покажем, что функция х1х2 двойственна к x1&x2, функция х1 х2 двойственна к функции x1|x2.
-
x1 x2
f=х1х2
f*
g=x1|x2
g*=x1 x2
0 0
0 1
1 0
1 1
0
1
1
1
0
0
0
1
1
1
1
0
1
0
0
0
Пример
4.
Построить формулу, реализующую f*,
если f
= ((x
y)
z)
(y
(xyz)).
Покажем, что она эквивалентна формуле
N
= z(xy).
Найдем (xy)* и (x y)*.
-
x y
xy
(xy)*
x y
(x y)*
0 0
0 1
1 0
1 1
0
1
1
0
1
0
0
1
1
1
0
1
0
1
0
0
Из таблиц видно, что
(x
y)*
= x
~ y
=
=
x
y
1,
x
y
=
y
x
,
(x
y)*
=
y
x
y
=
y.
По принципу двойственности:
f* =
yz
(
(x
(y
z)
1))
=
yz
z(x
(y
z)
1)
= z(
y(
x
z
))
= z(
y
(xz1))
= z(
y
(x
))
= z
y(z
xz
)
= z(
yx
)
= z(xy).
Тогда f = (f*)* = [z(xy)]* = z(x~y).
Задание 1 . Используя непосредственно определение двойственности булевых функций, выясните, является ли функция g двойственной к функции f:
1)
, 
;
2)
, 
;
3)
,
;
4)
, 
;
5)
, 
;
6)
, 
;
7)
, 
;
8)
, 
;
9)
,
;
10)
,
;
11)
,
;
12)
,
.
Задание 2 . Используя принцип двойственности, постройте формулу, реализующую функцию, двойственную к функции f, и убедитесь в том, что полученная формула эквивалентна формуле V:
1)
, 
;
2)
, 
;
3)
, 
;
4)
, 
;
5)
,
;
6)
, 
;
7)
, 
;
8)
, 
;
9)
, 
;
10)
, 
.
Задание 3 . Выяснить, является ли функция f самодвойственной:
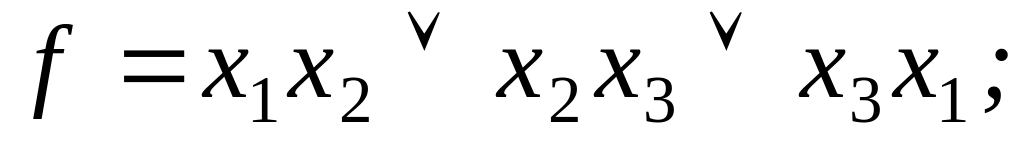
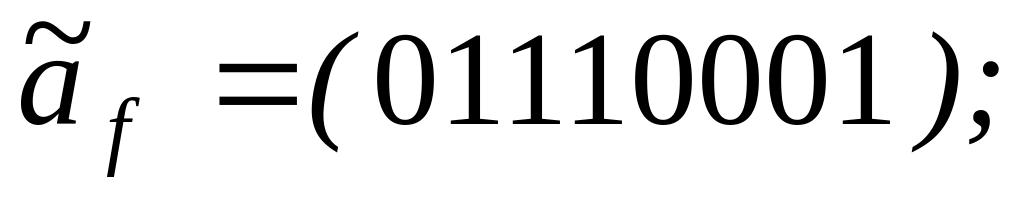
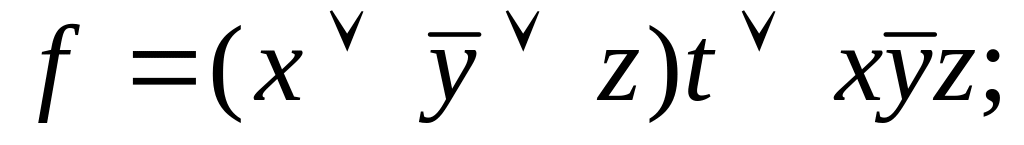
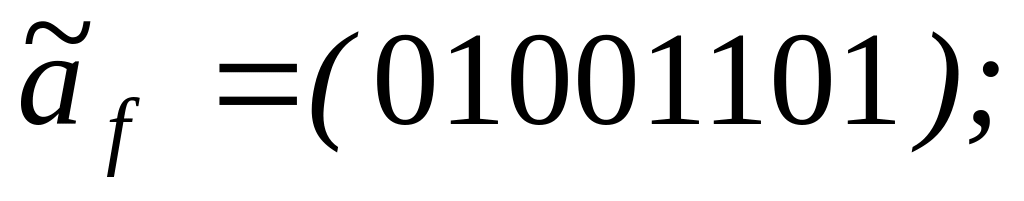
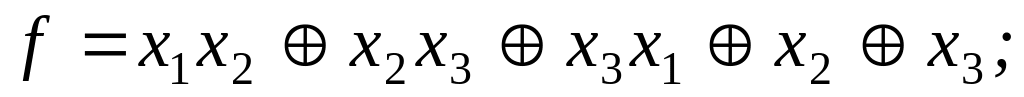
6)
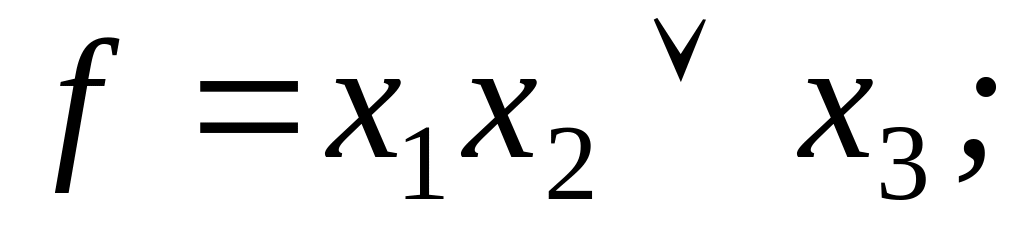
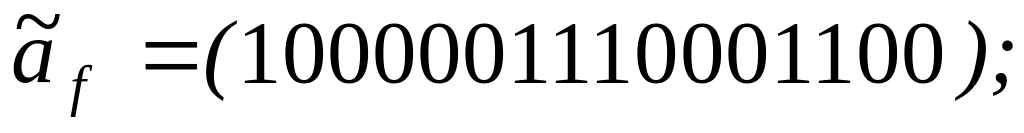
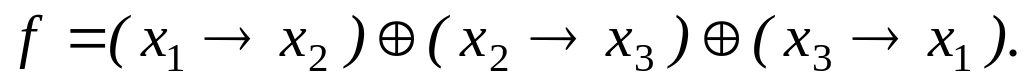
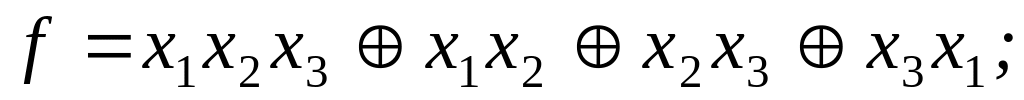
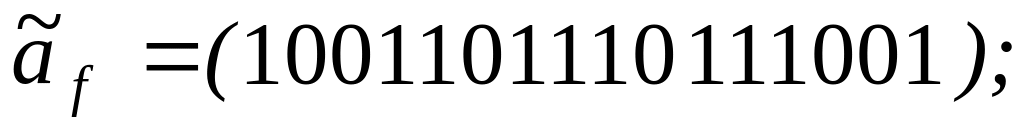
Задание 4 . Представив функцию f полиномом, выяснить, является ли она линейной:
