
5.4. Alternating current. The Ohm law for alternating current
Forced
electric oscillations can be considered as flow of alternating
current (ac) under the action of external EMF
![]() in
a closed electric circuit which consists of a capacitor, an
inductance coil, and an ohmic resistance. The current changes
according to harmonic law
in
a closed electric circuit which consists of a capacitor, an
inductance coil, and an ohmic resistance. The current changes
according to harmonic law
![]() its amplitude is
its amplitude is
![]() (2.58)
(2.58)
Denominator of equation (2.58)
![]() (2.83)
(2.83)
is cold total resistance or impedance.
Equation (2.58) is cold the Ohm law for alternating current.
If an electric circuit has an ohmic resistance only, equation (2.58) turns into
![]() (2.84)
(2.84)
Comparison
of equation (2.84) with (2.58) shows that disregard of an
inductance coil means that
![]() but disregard of a capacitor
means that
but disregard of a capacitor
means that
![]() (short-circuited capacitor).
(short-circuited capacitor).
If an electric circuit has an inductance coil only ( ), equations (2.58) and (2.60) give
![]() (2.85)
(2.85)
![]() Value
Value
![]() (2.86)
(2.86)
is cold inductive reactance.
Inductive reactance (2.86) is used for creation of chokes. They represent wire coils which are entered in an electric circuit where alternating current flows for regulation the current intensity. Chokes have advantage in comparison with rheostats as the increase of their resistance is not accompanied by increase of Joule heat, and so, useless Joule loss of energy is absent. Besides, inductive reactance exists only for alternating currents (inductance does not make resistance to direct current), chokes allow to divide direct and alternating currents.
According
to (2.86) inductive reactance
grows with increase of frequency; therefore, for very big frequencies
even small inductance represents significant resistance. Following
experiment proves it. Let a thick copper rod of 5 mm diameter and 1 m
length has the form of an arch abcde.
The rod is connected to a EMF source
which frequency
![]() (Fig. 2.12). An incandescent lamp is connected
to the arc in parallel. The copper arc resistance for direct current
is
(Fig. 2.12). An incandescent lamp is connected
to the arc in parallel. The copper arc resistance for direct current
is
![]() the lamp resistance
is 100
the lamp resistance
is 100
![]() Therefore, the arc
short-circuits the
lamp.
Therefore, the arc
short-circuits the
lamp.
But
for alternating current,
the arc has inductive reactance
![]() If
If
![]() ,
the arc resistance becomes very large and
the current totally flows through the
lamp giving rise to its bright shining.
,
the arc resistance becomes very large and
the current totally flows through the
lamp giving rise to its bright shining.
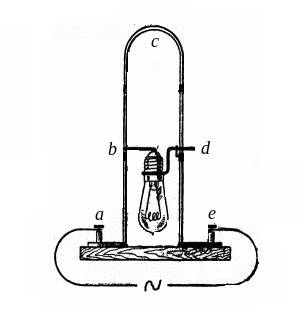
Fig. 2.12
If an
electric circuit has a capacitance only
(
![]() ),
equations (2.58) and (2.60) give
),
equations (2.58) and (2.60) give
![]() (2.87)
(2.87)
and
![]() Value
Value
![]() (2.88)
(2.88)
is cold capacitive resistance.
Direct current
![]() cannot flow through a capacitor.
cannot flow through a capacitor.
Equation (2.88) can be easy check up experimentally if we make an electric circuit which contains the variable capacitor and incandescent lamp connected in series, and connect the circuit to an alternating current source. Changing the capacity shows that the larger is the capacity the brighter is the lamp shining and, hence, stronger is the current. Therefore, a capacitor resistance is inversely proportional to its capacity. Equation (2.88) shows that for alternating current at very high frequencies even small capacities have absolutely insignificant resistance. An interesting fact confirms it. Experimenter (Fig. 2.13) stands on an isolated bench with glass legs and touches through a conductor a lamp.
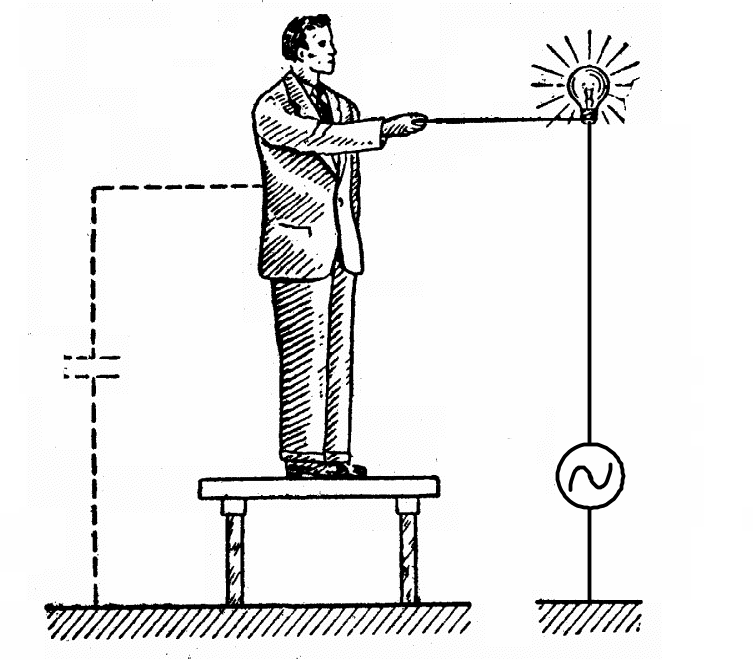
Fig. 2.13
The
second contact of the lamp is connected to a high-voltage source of
an alternating current with frequency
;
the other contact of the source earthed. It is obvious, that for
direct current the electric circuit is open. It is broken off by the
isolated bench. However, the lamp is brightly shining. It means that
the body of the experimenter and the ground represent a capacitor
plates; alternating current flows through the capacitor. Therefore,
the electric circuit that is open for a direct current appears closed
for alternating current. As the current frequency is very high, the
capacitor resistance![]() becomes so small, that relatively strong current can flow in the
circuit.
becomes so small, that relatively strong current can flow in the
circuit.
If an electric circuit has no ohmic resistance ( ), equation (2.58) changes into
![]() (2.89)
(2.89)
Value
![]() is cold reactance.
is cold reactance.
We
have considered different variants of electric
circuits connected to external alternating EMF. All above mentioned
equations are true for an electric
circuit sections if instead of the EMF
equation
we take the equation for voltage across the section
![]()
