5.2. Free damped electric oscillations

Any real oscillatory contour has resistance; hence its energy continuously transforms in heat; in some time, all energy transforms in heat, and oscillations end. The more is the resistance the less is the oscillations duration.

Equation (2.2) for damped electric oscillations takes the form

(2.22)

where  is damping coefficient,  is natural cyclic frequency if

Second-order differential equation is similar to equation of damped mechanical oscillations; therefore its solution at is

(2.24)

where

(2.25)

 is cyclic frequency of damped oscillations, and  are constants which depend on initial conditions. For damped electric oscillations

(2.26)

Damped electric oscillations period

(2.27)

is bigger than undamped electric oscillations period.

Damped electric oscillations amplitude is exponentially decreases with time. is initial amplitude.

Division of equation (2.24) by capacitance gives an equation of dependence voltage across the capacitor plates on time:

(2.28)

where  is initial amplitude of voltage across the capacitor plates.

Differentiation of equation (2.24) by time gives an equation of dependence current intensity in the coil on time

(2.29)

Damped oscillations amplitude decreases in times per time . The time is called relaxation time. Number of oscillations per the relaxation time is

Logarithmic decrement (damping constant) is equal to logarithm of relation of two adjacent amplitudes:

(2.35)

Therefore:

(2.36)

If damping is small

(2.38)

Quality factor or Q factor of oscillatory system is called Q of electrical circuit in radio engineering

(2.39)

If damping is small, we can use equation (2.38) to find Q (quality factor) of electrical circuit:

(2.40)

Energy of an oscillatory system is proportional to its amplitude squared; hence the energy reduces with time according to equation

If an electrical circuit resistance increases, its cyclic frequency decreases. When process of the capacitor discharge becomes aperiodic. The electrical circuit resistance at is called critical. Critical resistance can be calculated from (2.26) if

(2.42)

5.3. Forced electric oscillations

We get forced electric oscillations if we connect an electrical circuit to an external altering electromotive force (Fig. 2.2). If EMF changes accordingly to harmonic law ( ), equation (2.2) becomes

(2.48)

By analogy with forced mechanic oscillations partial solution of (2.49) is

(2.50)

where

(2.51)

(2.52)

Substitution and in (2.51), (2.52) gives

(2.53)

(2.54)

Substitution (2.53), (2.54) in (2.50) gives

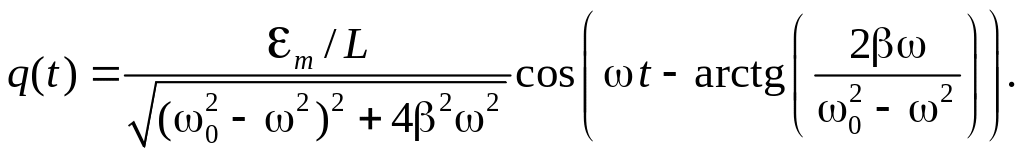(2.56)

the current amplitude

(2.58)

Analysis shows that voltage across the capacitor plates phase lag behind the current phase by voltage across the inductance coil phase leads current phase by voltage drop across ohmic resistance has the same phase as the current.

Phase relations of electric oscillations can be shown graphically by vector diagram. We take a vector which length is equal to amplitude; it creates an angle with horizontal axis (current axis) which is equal to initial phase (Fig. 2.7). According to second Kirchhoff’s law therefore EMF is result of additions of three vectors

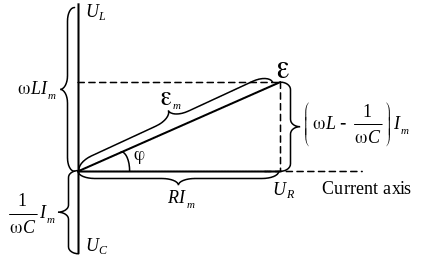
Fig. 2.7

Analysis of equation (2.51)

shows that amplitude reaches maximum at some cyclic frequency of external EMF (Fig. 2.8). The phenomenon is called resonance.

Resonance frequency

Fig. 2.8

(2.67)

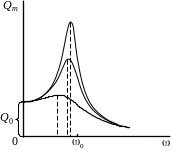
If

Substitution (2.67) in (2.51) gives resonance amplitude equation

(2.68)

We can see that resonance amplitude becomes infinite if

Let us analyze phase shift between current and external EMF using equation (2.60)

Its numerator is called reactance.

If is big and negative; hence, (current phase leads external EMF phase). If the frequency increases, the reactance and phase shift decreases up to zero When , we get condition of resonance ( ).

Then reactance becomes positive and increases with Hence, If external EMF phase leads current phase.

Dependence the phase shift on frequency is shown on Fig. 2.10. The less is the damping coefficient the sharper is the phase shift near resonance frequency

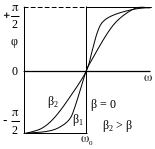
Fig. 2.10

If

Width of resonant zone is

,

where and are cyclic frequencies on the slopes of the resonance curve (Fig. 2.9) where energy of oscillations is half of oscillations energy at resonance frequency. Energy of electric oscillations is proportional to squared amplitude of current intensity; hence, current amplitudes at frequencies and are (Fig. 2.11). If ratio of energies equals 0.5, ratio of amplitudes equals (Fig. 2.11).

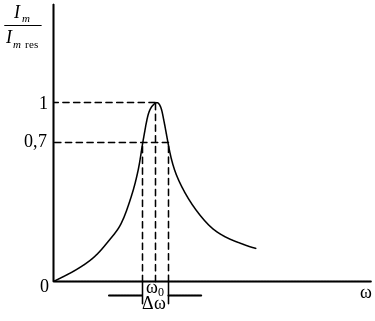
Fig. 2.11

The resonance phenomenon is used for allocation from a complex signal a necessary component. The principle of action a radio receiver is based on a resonance. A radio receiver has to be tuned in to a radio station, i.e. to achieve concurrence of the natural frequency of an oscillatory contour of a radio receiver to frequency of electromagnetic waves which radiates the certain radio station. Sensitivity of a radio receiver is proportional to the quality factor of a contour. The radio receiver of high sensitivity is capable to accept very narrow strip of frequencies. The lager is sensitivity of a radio receiver, the less other radio stations which work on close frequencies interfere in acceptance of a signal of the selected radio station.