Навчальний
елемент 2
5. Electric oscillation
5.1. Free (natural) electric oscillations
An oscillatory contour is a capacitor with capacity C, a coil with inductance L, and a conductor with ohmic resistance R connected in series. Electric oscillation of a contour means periodic change of a charge on the capacitor plates and a current in the inductance coil. Periodic changes of a charge and current cause changes of electric and magnetic fields energy, therefore there are electromagnetic oscillation.
Let's
consider an ideal electric oscillatory contour with the parameters C,
L and
(Fig. 2.1, a).
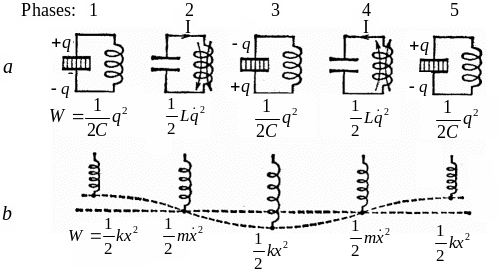
Fig. 2.1
Oscillation
in the contour can be caused, if we attach the capacitor to a source
of a voltage; as a result, opposite charges
and
on the capacitor plates appear and ,accordingly, an electric field
with energy
creates in the capacitor, (Fig. 2.1, a; phase 1, the moment of time
If then we disconnect the source and connect the capacitor to the
inductance, the capacitor begins to discharge and a current begins to
flow in the contour; the current can not at once get the maximal
value. The reason of it is the current of a self-induction which
arises in inductance and directed against a growing current according
to Lentz rule. Discharge of the capacitor is accompanied by reduction
of absolute value of the capacitor plates charge and energy of the
electric field. The process is accompanied by occurrence of the
magnetic field caused by a current which flows through inductance.
The current increases; therefore, energy of a magnetic field
created by the inductance coil also increases.
As
the resistance
the
full energy of electric and magnetic fields is not spent for heating
of conductors. It means that it remains constant. Therefore, at the
moment of time when the capacitor is discharged, energy of an
electric field is equal to zero, the current in the inductance
becomes maximal, and so, magnetic field energy reaches the maximal
value (Fig. 2.1, a; phase 2, the moment of time
)
The current starts to fall down without changing a direction from
this moment. However, it does not fall to zero at once as EMF of
self-induction prevents to this. The current will charge the bottom
plate of the capacitor positively, and the top plate – negatively;
it will occur until charges on the capacitor plates reach initial
absolute values, but signs of charges on the capacitor plates
exchanges.
Current
in the contour equals zero when the moment of time
,
and the magnetic energy of the coil completely turns into an electric
energy of the capacitor (fig. 2.1, a; phase 3). Then, the capacitor
begins discharge again. But direction of the discharge current flow
will be opposite to a direction of the discharge current at phase 2.
Oscillatory processes repeat in the opposite direction (fig. 2.1, a;
phases 4 and 5, the moments of time
and
In time
the
oscillatory contour comes back in an initial state. Process of
periodic transformation of energy of an electric field into energy of
a magnetic field and on the contrary can last for an infinitely long
time if
.
Oscillations in a contour without external influences and losses of energy are named free or natural undamped (continuous) electric oscillation. The oscillatory process represents periodical changes of a charge and a voltage across the capacitor plates, and a current intensity which passes through the inductance.
Fig.
2.1, b
shows analogy between electric oscillations and oscillations of a
spring pendulum. A charge on the capacitor plates is analogical to
the pendulum displacement
.
The pendulum elastic deformation energy
is similar to the capacitor electric field energy
.
The pendulum kinetic energy
is similar to the coil magnetic field energy
Mathematical expressions that describe mechanical and electric
oscillations are very similar too.
Let us consider an oscillatory contour which consists of a capacitor with capacity C, a coil with inductance L, and a conductor with ohmic resistance R connected in series to a source of periodical external electromotive force (Fig. 2.2).
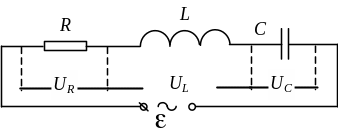
Fig. 2.2
According
to second Kirchhoff’s law, the EMF
equals the sum of voltage drops across the capacity
the
inductance
,
and the resistance
(2.1)
The
capacitor charge change
per time
equals
hence
(2.2)
If
we take
and
we get free or natural undamped electric oscillations (Fig. 2.1)
which equation is
(2.3)
where
is cyclic frequency of natural undamped
electric oscillations. Therefore,
natural undamped electric oscillations
period
(2.5)
Equation (2.5) is named after Thomson.
Let us remember that equation (2.4) is a harmonic oscillator equation; its solution is sinusoidal or cosine function of dependence the capacitor charge on time
(2.6)
The oscillations
amplitude
and
initial phase
are
constant. Amplitude
equals the maximal charge on the capacitor plates.
Using (2.6), we can find dependence voltage-time for the capacitor:
(2.10)
where
is
amplitude voltage.
Differentiation of equation (2.6) by time gives dependence current-time
(2.11)
where
is
amplitude current intensity.
The phase of
current intensity in the inductance coil leads the phase of voltage
across the capacitor plates by
When the current is maximal
the voltage becomes zero and vice versa.
Decrease of the capacitor electric field energy leads to increase of the coil magnetic field energy
. (2.12)
According to energy conservation law, maximal energy of electric field equals maximal energy of magnetic field
(2.14)
Dependences of
energies of electric and magnetic fields on time are following
(remember that
:
(2.15)
(2.16)
Analysis of equations (2.15) and (2.16) shows that total energy of natural undamped electric oscillations remains the same
; (2.17)
it is proportional to the amplitude squared.