1.8 Интегрирование некоторых классов иррациональных функций

Если под знаком интеграла стоит иррациональная функция, то в ряде случаев удаётся, пользуясь преобразованием переменной, привести подинтегральную функцию к рациональному виду и вычисление заданного интеграла свести к вычислению интеграла от рациональной функции.

Ниже перечислены те классы иррациональных функций, которые после соответствующего преобразования переменной могут быть сведены к рациональным функциям.

1-й случай. Если под знаком интеграла стоит рациональная функция от дробных степеней независимой переменной , т.е. функция , то такая функция всегда может быть преобразована в рациональную форму при помощи подстановки , где есть общее наименьшее кратное всех знаменателей дробных показателей , т.е. есть общее наименьшее кратное чисел

Таким образом, указанный выше приём применим к интегралам типа

Пример 20 Вычислить интеграл

Решение. Под интегралом стоит рациональная функция от дробных степеней . Общее наименьшее кратное знаменателей равно 12, а потому полагаем Подставив в подинтегральное выражение и , получаем:

(подставляем значение )

Этот интеграл можно было вычислить быстрее, если свести его к интегрированию степенных функций, разделив числитель на знаменатель.

2-й случай. Если под знаком интеграла стоит рациональная функция от и дробных степеней дробно линейной функции т.е. , то подстановкой , где есть общее наименьшее кратное знаменателей данная функция будет преобразована в рациональную форму.

Пример 21 Вычислить интеграл

Решение. Полагаем следовательно, и получаем:

3-й случай. Интегралы типа

а) Если под знаком интеграла содержатся только радикалы вида , при условии , то подинтегральное выражение можно представить в рациональной форме при помощи подстановки (подстановка Эйлера).

Замечание. Следует отметить, что эта подстановка часто приводит к очень громоздким выкладкам, а потому пользоваться ею следует только в крайних случаях, т.е. тогда, когда трудно указать другие способы для вычисления данного интеграла. Это же замечание относится и к подстановкам, которые даются далее при рассмотрении случаев .

Пример 22 Вычислить интеграл

Решение. Под интегралом не содержится иных радикалов, кроме радикала указанного выше вида, и при этом Преобразуем подинтегральное выражение в рациональную форму, пользуясь подстановкой

Возводя в квадрат обе части равенства (1), выразим :

Следовательно,

Выполнив подстановку, получим:

b) Если под знаком интеграла содержатся только радикалы вида , то при условии подинтегральное выражение можно привести к рациональному виду при помощи подстановки (подстановка Эйлера).

Пример 23 Вычислить интеграл

Решение. В данном примере подинтегральное выражение содержит только радикалы указанного вида, причём , а потому применим подстановку

Отсюда определяем , возводя обе части равенства в квадрат.

Получаем:

Следовательно,

Выполнив подстановку, получим:

c) Если под знаком интеграла содержатся только радикалы вида и 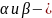действительные корни трёхчлена , то подинтегральное выражение можно привести к рациональному виду при помощи подстановки (подстановка Эйлера).

Пример 24 Вычислить интеграл

Решение. Трёхчлен имеет два действительных корня , а следовательно, интеграл можно вычислить с помощью подстановки

Возводим в квадрат обе части последнего равенства и определяем :

Отсюда:

Выполнив подстановку, получим:

Дифференциал вида какие угодно постоянные, а показатели числа рациональные, называется биномиальным дифференциалом. П. Л. Чебышев доказал, что если под знаком интеграла стоит биномиальный дифференциал, то интеграл выражается в элементарных функциях в следующих случаях:

1-й случай. а) Если p – целое положительное число, то под интегралом нужно раскрыть скобки по правилу бинома Ньютона и затем вычислять полученный интеграл.

Пример 25

b) Если p – целое отрицательное число, то при интегрировании применяется подстановка общий знаменатель дробей . Такая подстановка приводит подинтегральное выражение к рациональному виду.

Пример 26 Вычислить интеграл

Решение. В данном случае а потому применим подстановку , так как общий знаменатель дробей равен двум; Получаем:

2-й случай. Если в дифференциальном биноме числа таковы, что целое число, то интеграл вычисляется при помощи подстановки знаменатель дроби числа p.

Пример 27 Вычислить интеграл

Решение. В данном примере Так как целое число, то следует применить подстановку знаменатель числа . Решая последнее равенство относительно , получаем

Выполнив подстановку, получим:

так как

3-й случай. Если числа , входящие в дифференциальный бином, удовлетворяют условию, что число целое, то в этом случае интеграл вычисляется при помощи подстановки знаменатель числа

Пример 28 Вычислить интеграл

Решение. Так как то

В данном случае есть целое число, а потому для вычисления интеграла применим подстановку так как знаменатель числа равен двум.

Решая последнее равенство относительно , получаем:

Подставляем найденные значения в подинтегральное выражение и вычисляем интеграл: