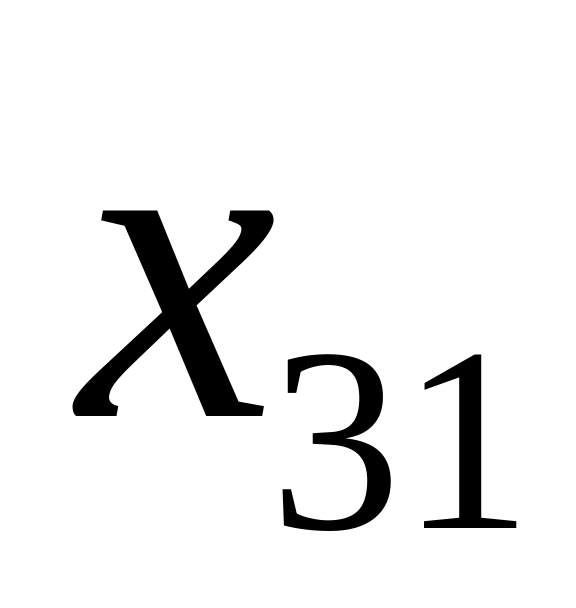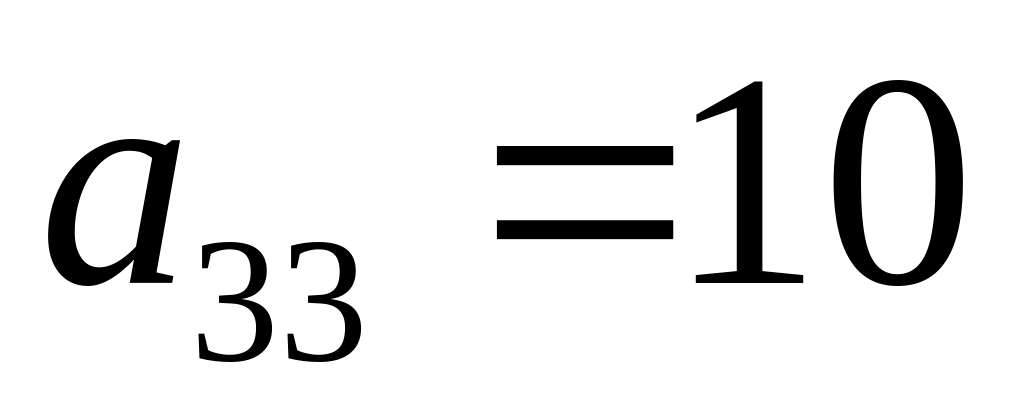Контрольные вопросы:
Чем отличается данная ТЗ от предыдущей?
Объясните расчет ограничений по числу автомобилей.
Как рассчитать объем перевозок конкретным типом автомобиля по конкретной линии?
Объясните почему полученная матрица решений оптимальна.
Задача 3 (о назначениях). Задача о назначениях одна из разновидностей задач распределительного типа (ЗРТ), в которой для выполнения каждой работы требуется один и только один ресурс (один работник, один станок, одна автомашина и т.д.). Другими словами, ресурсы не делимы между работами, а работы не делимы между ресурсами. Таким образом, задача о назначениях является частным случаем ТЗ, рассматривающая назначение сотрудников на должности или работы, автомашин на маршруты, водителей на автомашины и т.п.
Решение: Экономико-математическая модель задачи.
Пусть
на автопредприятии (или в подразделении
автопредприятия) имеются
водителей
,
,
…,
,
…,
,
которых необходимо назначить (распределить)
по
маршрутам
,
,
…,
,
…,
.
На каждом из указанных маршрутов может
работать любой из этих водителей, однако
выручка по разным водителям и по разным
маршрутам различается. В результате
проведенных наблюдений зафиксирована
выручка водителей по разным маршрутам.
Обозначим
выручку
-го
водителя по
-му
маршруту, а
назначение
-го
водителя на
-й
маршрут:
=
Условие задачи о назначениях можно представить в табличном виде (табл. 4).
Из
табл. 4 следует, что если водитель
назначен на маршрут
,
то
,
а остальные элементы этой строки будут
равны 0. Таким образом, сумма переменных
для любой строки или столбца равна 1,
т.е. можно записать следующие условия:
(6.1)
В
качестве целевой функции (критерия
оптимальности) принимаем суммарную
производительность сотрудников:
(6.2)
Таким
образом, сущность задачи о назначениях
состоит в отыскании таких неотрицательных
значений
,
чтобы целевая функция (общая выручка)
была максимальной.
Таблица 4
Условие задачи о назначениях
Водители |
Маршруты |
|||||
R1 |
R2 |
… |
Ri |
… |
Rn |
|
S1 |
|
|
… |
|
… |
|
S2 |
|
|
… |
|
… |
|
… |
… |
… |
… |
… |
… |
… |
Si |
|
|
… |
|
… |
|
… |
… |
… |
… |
… |
… |
… |
Sn |
|
|
… |
|
… |
|
Рассмотренную выше задачу можно классифицировать как комбинаторную (переборную) задачу. Пример решения подобной задачи представлен ниже.
Задача 3.1. На малом автопредприятии имеются три водителя, которых необходимо распределить по трем различным маршрутам. Предварительно была определена выручка каждого водителя по каждому из трех маршрутов (табл. 5).
Таблица 5
Выручка каждого водителя по каждому из трех маршрутов
-
Работники
Работы
R1
R2
R3
S1
S2
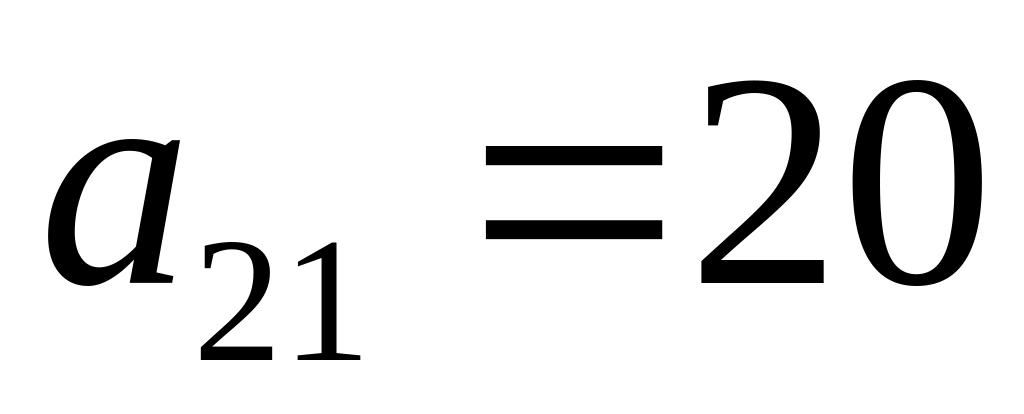
S3
